
Урок «Элементы симметрии правильных многогранников»

Краткое описание документа:
ТЕКСТОВАЯ РАСШИФРОВКА УРОКА:
Наше знакомство с многогранниками продолжается.
Вспомним, что многогранник называется правильным, если выполнены следующие условия:
1.многогранник выпуклый;
2. все его грани являются равными правильными многоугольниками;
3. в каждой его вершине сходится одинаковое число граней;
4. все его двугранные углы равны.
На прошлых занятиях вы узнали об единственности существования пяти видов правильных многогранников:
тетраэдра, октаэдра, икосаэдра, гексаэдра(куба) и додекаэдра.

Сегодня мы рассмотрим элементы симметрии изученных правильных многогранников.
Правильный тетраэдр не имеет центра симметрии.
Его осью симметрии является прямая, проходящая через середины противоположных рёбер.
Плоскостью симметрии является плоскость, проходящая через любое ребро перпендикулярно противоположному ребру.
Правильный тетраэдр имеет три оси симметрии и шесть плоскостей симметрии.
Куб обладает одним центром симметрии- это точка пересечения его диагоналей .
Осями симметрии являются прямые проходящие через центры противоположных граней и середины двух противоположных рёбер, не принадлежащих одной грани.
Куб имеет девять осей симметрии, которые проходят через центр симметрии.
Плоскость, проходящая через любые две оси симметрии, является плоскостью симметрии.
Куб имеет девять плоскостей симметрии.
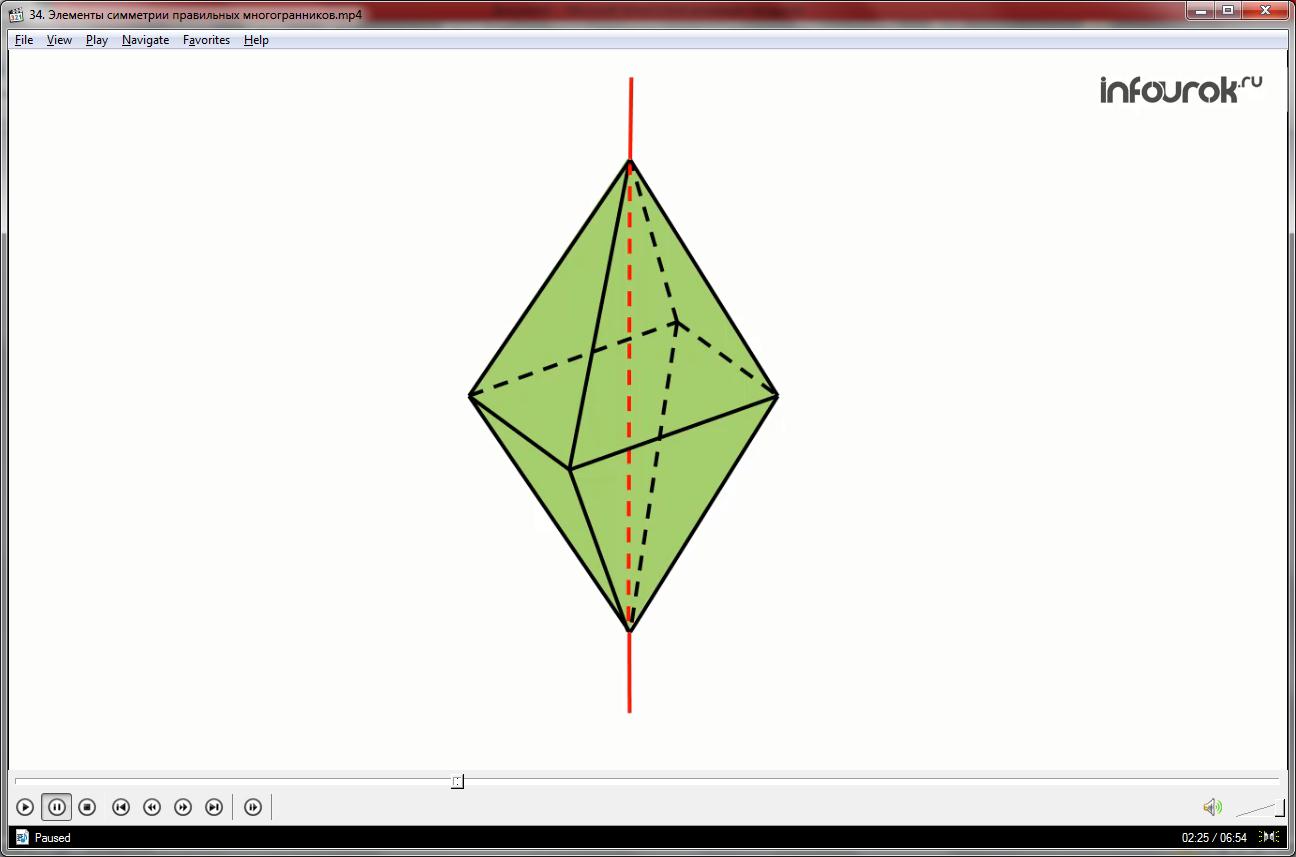
Правильный октаэдр имеет центр симметрии - центр октаэдра, 9 осей симметрии и 9 плоскостей симметрии: три оси симметрии проходят через противоположные вершины, шесть - через середины ребер.
Центр симметрии октаэдра - точка пересечения его осей симметрии.
Три из 9 плоскостей симметрии тетраэдра проходят через каждые 4 вершины октаэдра, лежащие в одной плоскости.
Шесть плоскостей симметрии проходят через две вершины, не принадлежащие одной грани, и середины противоположных ребер.
Правильный икосаэдр имеет 12 вершин. Икосаэдр имеет центр симметрии - центр икосаэдра, 15 осей симметрии и 15 плоскостей симметрии: Через первую пару противоположных вершин проходят пять плоскостей симметрии (каждая их них проходит через ребро, содержащее вершину, перпендикулярно противоположному углу).
Далее, через вторую пару противоположных вершин также проходят 5 плоскостей, но одна из них подсчитана в первом случае, так что остаются новых четыре плоскости симметрии.
Для третьей пары получим — 3 новых плоскости, а для четвертой — две плоскости и для пятой пары только одна новая плоскость.
Через шестую пару вершин не пройдет ни одной новой плоскости симметрии.
Правильный додекаэдр состоит из двенадцати правильных пятиугольников. Додекаэдр имеет центр симметрии - центр додекаэдра, 15 осей симметрии и 15 плоскостей симметрии: плоскости симметрии проходят через ребро, содержащее вершину, перпендикулярно противоположному ребру. Поэтому через первую пару противоположных пятиугольников проходит 5 плоскостей, через вторую пару — 4, через третью — 3, четвертую — 2, пятую — 1.
Решим несколько заданий, применяя полученные знания.
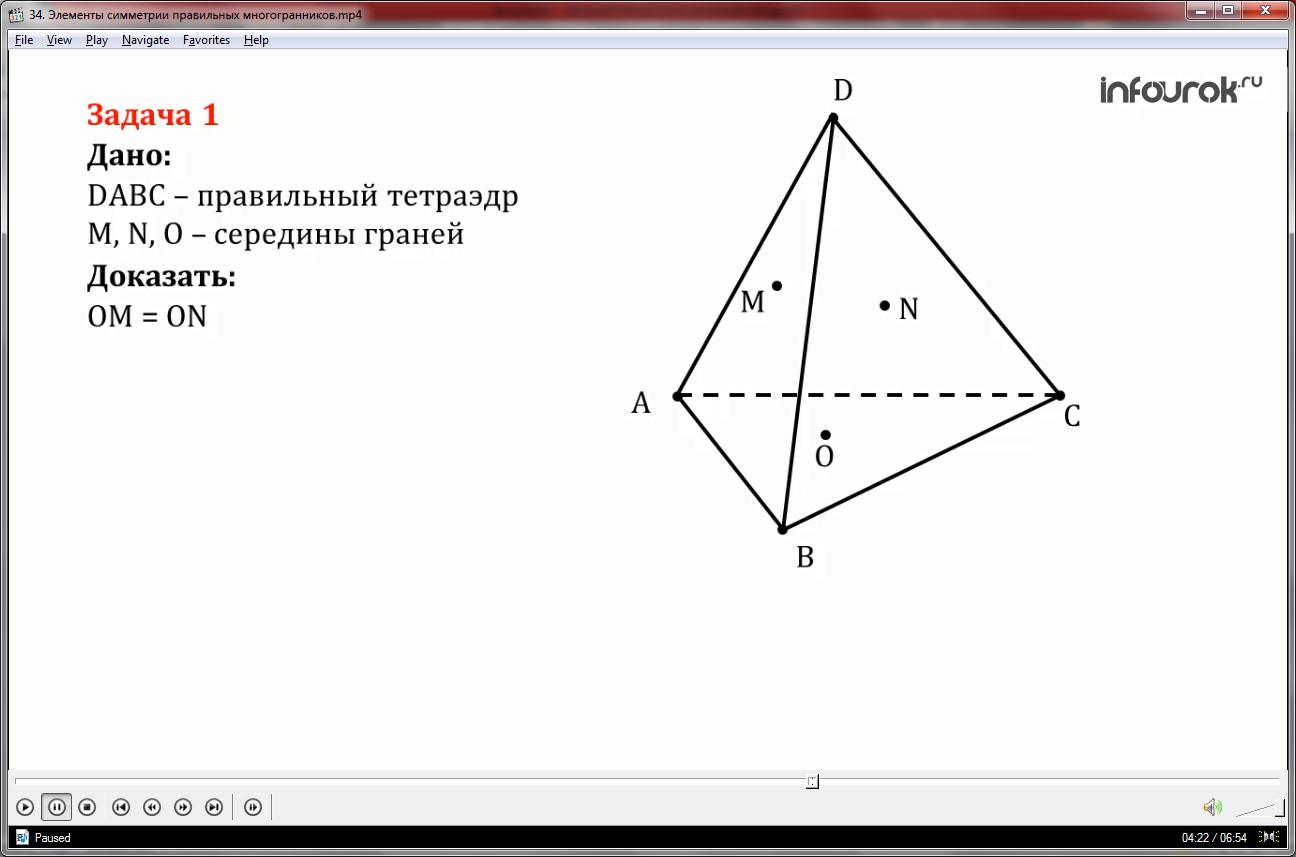
Задача 1.
Доказать, что в правильном тетраэдре отрезки, соединяющие центры его граней, равны.
Так как все грани правильного тетраэдра равны и любая из них может считаться основанием, а три другие- боковыми гранями, то достаточно будет доказать равенство отрезков ОМ и ON.
Доказательство:
1.Дополнительное построение: проведём прямую DN до пересечения со стороной АС, получим точку F;
проведём прямую DM до пересечения со стороной АВ, получим точку Е.
Затем соединим вершину А с точкой F;
вершину С с точкой Е.
2.Рассмотрим треугольники ДЕО и ДОФ они
прямоугольные, т.к. ДО высота тетраэдра, тогда они равны по гипотенузе и катету: ДО–общая, ДЕ=ДФ(высоты равных граней тетраэдра)).
Из равенства данных треугольников следует, что OE=OF, ME=NF(середины равных сторон),
угол DEO равен углу DFO.
3. из выше доказанного следует что треугольники ОЕМ и ОФН равны по двум сторонам и углу между ними (см пн. 2).
А из равенства этих треугольников следует, что ОМ = ON.
Что и требовалось доказать.
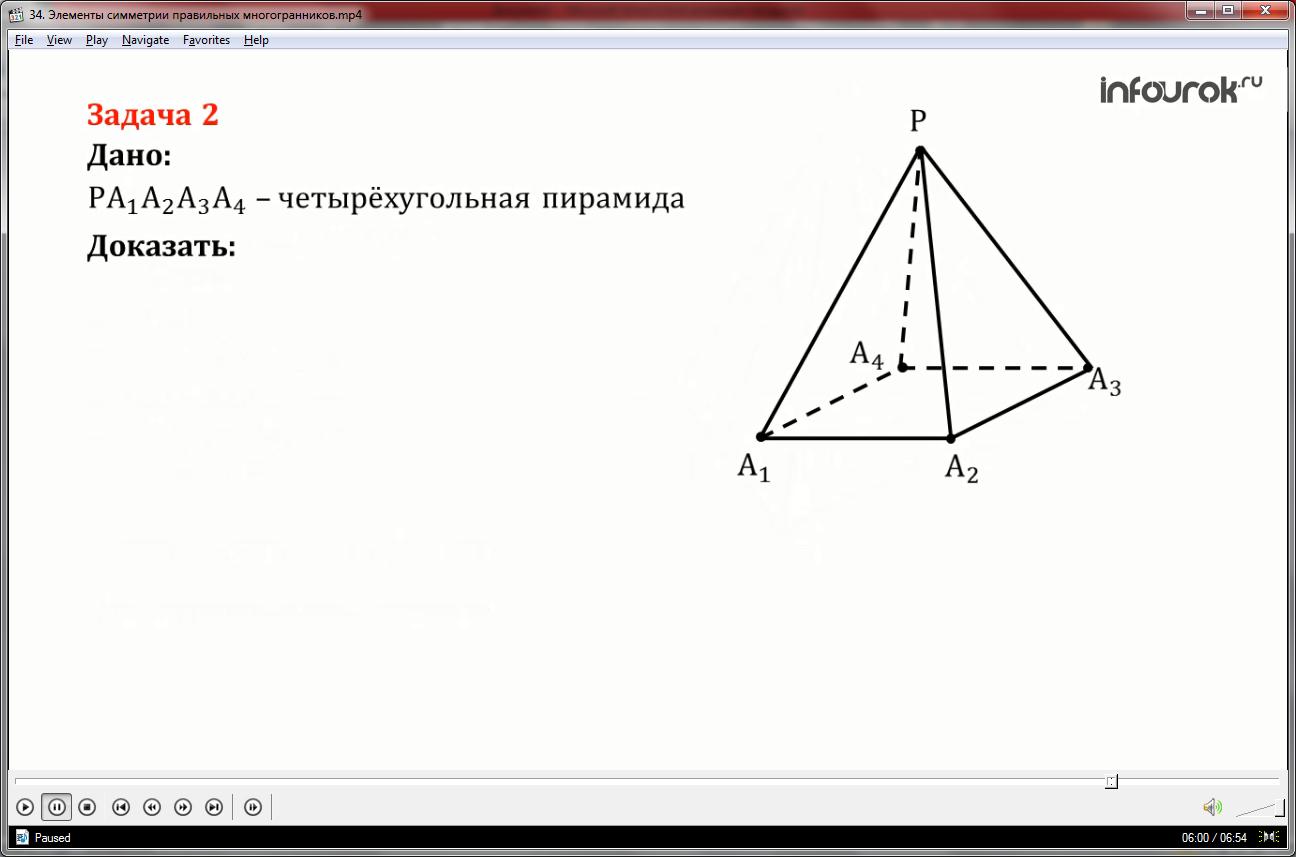
Задача 2.
Существует ли четырёхугольная пирамида, у которой противоположные грани перпендикулярны к основанию?
Докажем, что такой пирамиды не существует методом от противного.
Доказательство:
1. Пусть ребро РА1 перпендикулярно основанию пирамиды и ребро РА2 так же перпендикулярно основанию.
2.Тогда по теореме(две прямые, перпендикулярные к третьей, параллельны), мы получим что ребро РА1 параллельно ребру РА2.
3.Но пирамида имеет общую точку для всех боковых рёбер(а значит и граней)- вершину пирамиды.
Мы получили противоречие, таким образом не существует четырёхугольной пирамиды, противоположные грани которой перпендикулярны к основанию.
| Автор | |
|---|---|
| Дата добавления | 28.10.2014 |
| Раздел | Геометрия |
| Подраздел | Видеоурок |
| Просмотров | 13736 |
| Номер материала | 948 |