
Урок «Графики функций y=ax^2+n и y=a(x-m)^2»

Краткое описание документа:
Урок по теме «Графики функций y=ax^2+n и y=a(x-m)^2» изучается в системе уроков по теме «Функции» в 9 классе. До этого обучающиеся должны уже быть знакомы с функцией y=ax^2 и ее свойствами. Урок по теме, изучающей эту функцию можно найти также в нашей базе.
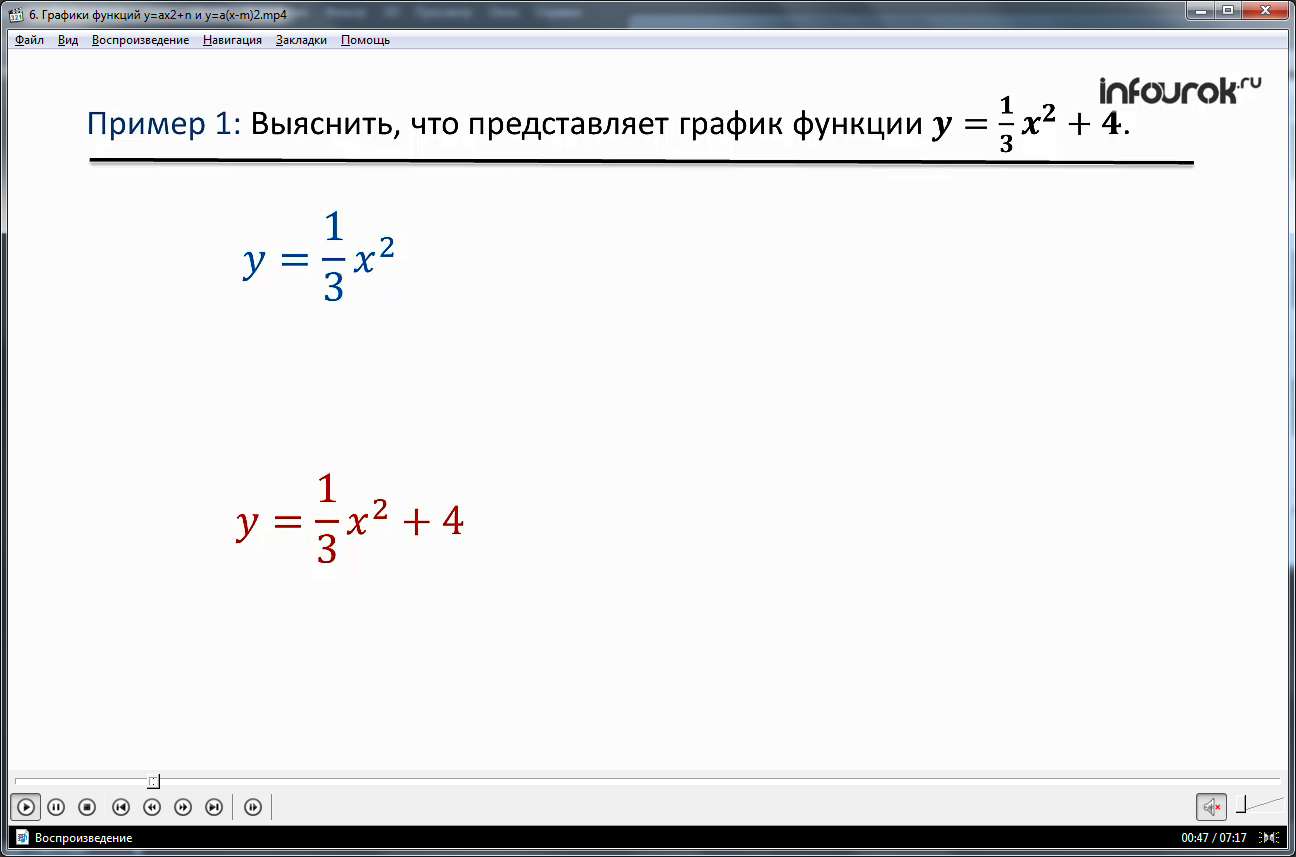
Начало урока посвящается примеру, где требуется определить, каким будет график заданной функции. Автор предлагает решать поставленную задачу поэтапно. Сначала построить график уже известной функции y=1/3 x^2, составив для нее таблицу значений, а затем построить график функции для y=1/3 x^2+4. Исходя из увиденного, автор делает вывод, что график последней функции получается из предыдущего путем поднятия его на 4 единицы вверх.
После этого автор приходит к общим словам, согласно которым обучающиеся знакомятся с правилом построения графика функции y=ax^2+n. В этом случае исходный график, а именно, график функции y=ax^2 посредством параллельного переноса перемещается на |n| единиц вверх или вниз, в зависимости от знака числа n.
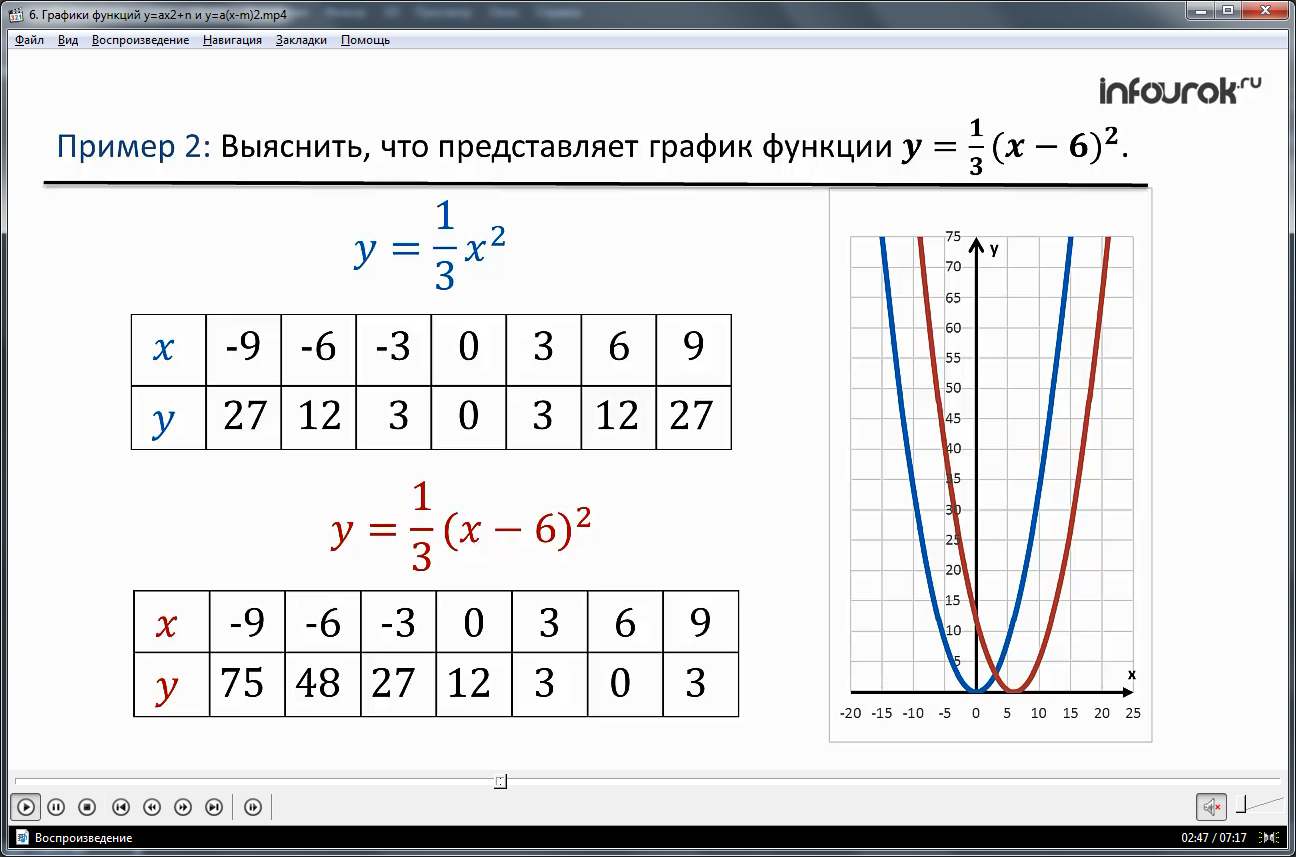
Далее автор рассматривает второй случай. И опять же с примера. Сначала предлагается снова построить график функции y=1/3 x^2, предварительно составив таблицу значений. А затем аналогично построить график функции y=1/3 (x-6)^2. После того, как графики построены, становится ясной картина: график второй функции получается из графика первой функции путем перемещения его вдоль оси x. Все это хорошо видно из рисунка на экране.

Затем обучающиеся могут познакомиться с этой ситуацией в общем виде. Математическим языком автор объясняет, что график функции y=a(x-m)^2 легко получить из графика функции y=1/3 x^2, совершив параллельный перенос вдоль оси x на |m| единиц в направлении, противоположном знаку числа m.
Объединив два первых случая, автор предлагает рассмотреть третий пример, где необходимо построить график функции y=1/3 (x-2)^2+5. Автор предлагает изобразить сначала график функции y=1/3 x^2, а затем использовать только что полученные знания. А именно, построить график функции y=1/3 (x-6)^2, сдвинув исходный график на 6 единиц вправо вдоль оси x. А затем уже в этой же системе координат построить график функции y=1/3 (x-2)^2+5, сместив предыдущий график на 5 единиц вверх вдоль оси y. Все три графика изображены на экране в одной системе координат. Чтобы обучающиеся смогли легко отличить их друг от друга, они выделены разным цветом.
Далее автор вводит проблемный вопрос, на который будет дан ответ в ходе дальнейших рассуждений. Чтобы ответить на поставленный вопрос, автор предлагает рассматривать каждый случай по отдельности. Эти случаи рассматриваются в общем виде, не используя конкретных числовых значений. По ходу выяснения истины, автор подробно останавливается на каждой ситуации. Все, что появляется на экране, он комментирует словами, поясняя более сложные моменты.
В ходе получения ответа на вторую часть вопроса, где речь идет о перемещении графика функции вдоль оси x, но в противоположном направлении, нежели знак числа m, автор знакомит обучающихся с понятием и фигурой параболоид. Здесь же указываются его свойства.
В ходе объяснения материала автор использует историческую справку, которая связывает понятия математики, а именно алгебру, с историей математики. Важную роль в то время сыграла деятельность древнегреческого математика Архимеда. Два рассмотренных свойства параболоида широко применяются в наше время в повседневной жизни и в быту. Это продемонстрировано также на экране.
На этом урок завершается. Его длительность составляет 7:16 минут. Этого времени достаточно для того, чтобы школьники усвоили материал, а затем приступили к его закреплению. Задания для закрепления необходимо подобрать учителю, который будет использовать данный видеоурок на занятии.
| Автор | |
|---|---|
| Дата добавления | 29.08.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 8390 |
| Номер материала | 677 |