
Урок "Измерительные работы"

Краткое описание документа:
Видеоурок «Измерительные работы» демонстрирует практическую ценность изученного материала. В состав видео входит демонстрация, каким образом можно измерить высоту предметов, применив имеющиеся знания их геометрии. Также знания геометрии помогут найти расстояние до недоступной точки. Практическое значение раздела математики о решении треугольников трудно переоценить. В строительстве, землемерных и других инженерных работах нередко применяются знания из этой области математики.
Применение теоретических знаний на практике демонстрируется при помощи иллюстраций, на которых легко изобразить реальную практическую задачу, возникшую в ходе инженерных работ. Анимированное представление построений дает возможность выявить знакомые задачи в ходе выполнения практического задания. При помощи сопровождения в виде формул и голосового объяснения дается развернутое объяснение метода решения подобных задач.
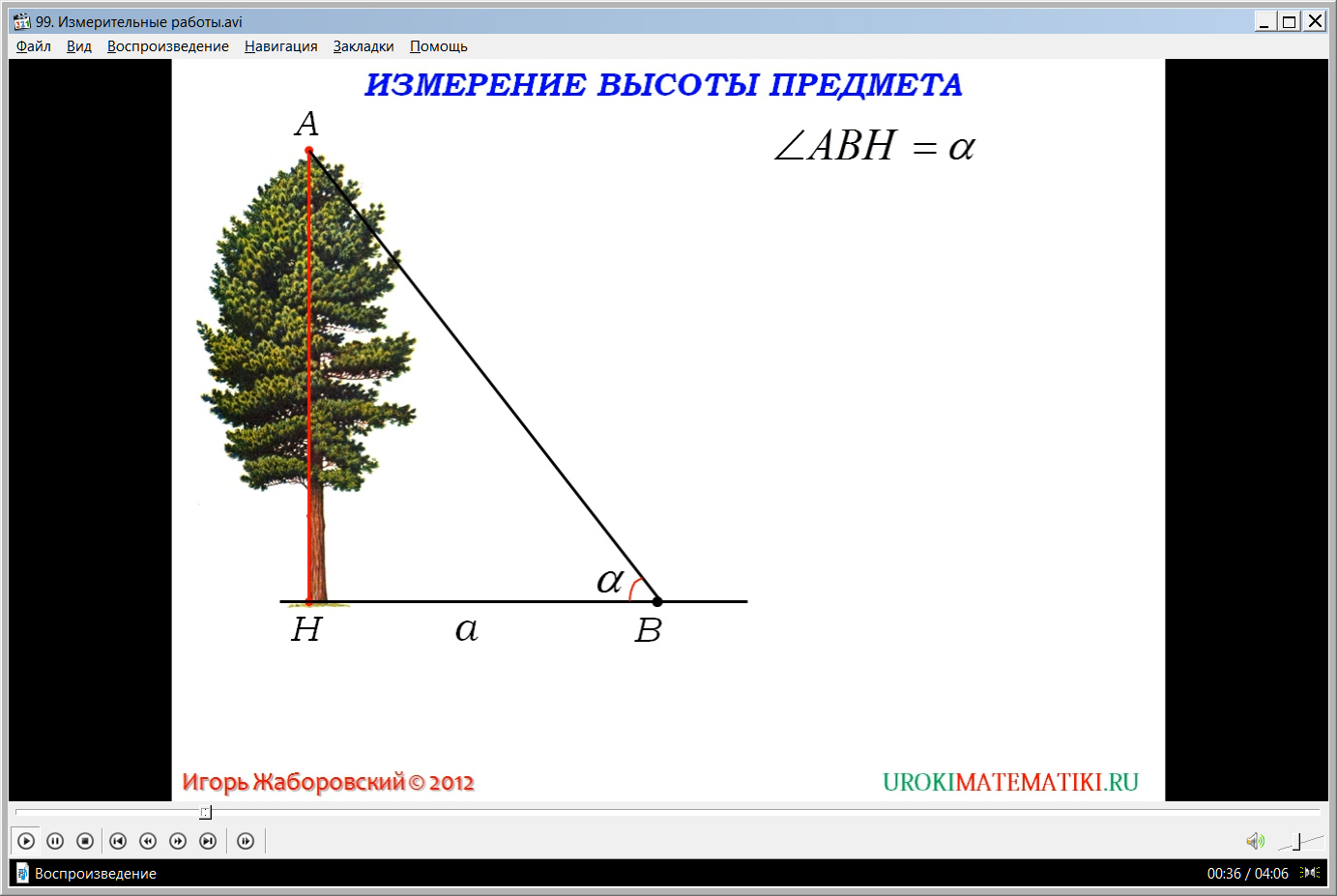
Видеоурок начинается с представления темы. Предлагается применить изученные материалы при решении практической задачи на местности – найти высоту некоторого предмета. На иллюстрации демонстрируется высокое дерево, высоту которого требуется измерить. Основание дерева отмечено как точка Н. Замечено, что при отметке некоторой точки А, до которой вычисляется высота, и некоторой точки В на расстоянии b от точки Н, образуется треугольник АНВ, значение некоторых элементов которого известно. Известны прямой угол при вершине треугольника Н, угол ∠АВН=α при вершине В, сторона а. Чтобы найти высоту АН необходимо вычислить произведение длины стороны а и тангенса угла ∠α.
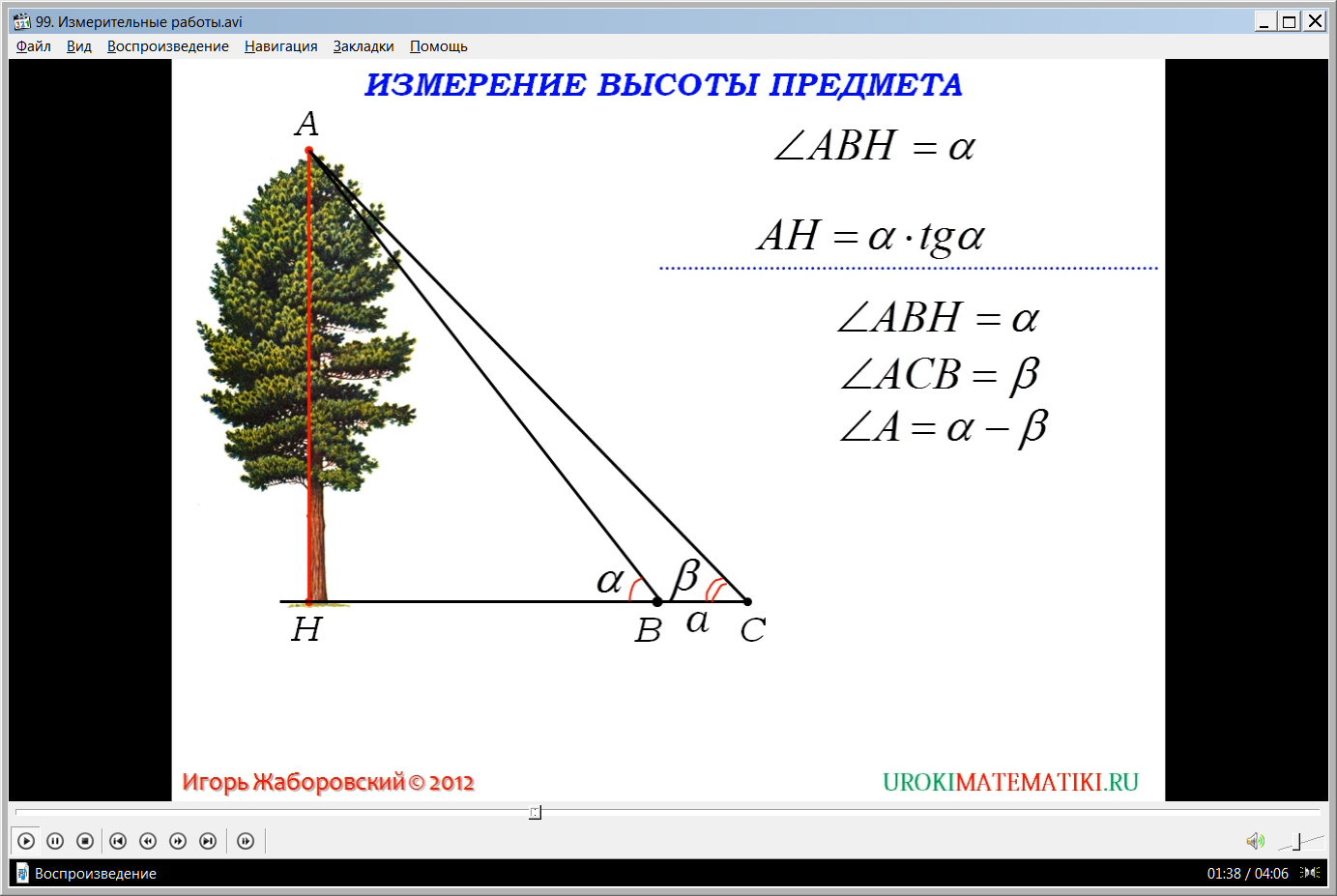
Решение задачи возможно даже в случае, когда нет возможности измерить расстояние от основания дерева Н до точки В. В этом случае на прямой, которой принадлежит сторона НВ, отмечается еще одна точка С. Измеряется расстояние а между отмеченными точками В и С, а также углы при них ∠АВН=∠α и ∠АСВ=∠β. Данных элементов достаточно, чтобы определить оставшиеся неизвестными элементы треугольника АВС. Так как ∠α является внешним углом треугольника, его величина определяется по формуле ∠А=α-β. Для нахождения длины стороны АВ применяем теорему синусов, из которой АВ=a·sinβ/sin(α-β). После вычисления стороны АВ можно определить высоту АН=АВ·sinα. Вместо АВ подставляется полученное выше выражение. Получаем высоту АН= a· sinα·sinβ/ sin(α-β).

Еще один вид задач, решаемых на местности с применением знаний, полученных в данном разделе – измерений расстояний от некоторой точки до недоступной точки. На рисунке к задаче приведен пример, когда необходимо измерить расстояние от некоторой точки до удаленной недоступной точки. Отмечена некоторая точка А, удаленная точка С и искомое расстояние d. Отмечается, что аналогичная задача уже решалась учениками в ходе курса математики с использованием понятия подобия треугольников. В этот раз демонстрируется решение задачи, используя методы решения треугольников. Для этого на данной местности отмечается еще одна точка В, от которой расстояние до А равно с. С помощью астролябии можно измерить углы при вершинах образованного треугольника ∠А=α и ∠В=β. Имеющихся данных достаточно, чтобы определить искомое расстояние d=АС. Оставшийся неизвестным угол ∠С вычисляется по теореме суммы углов треугольника sinС=sin(180⁰-α-β)= sin(α+β). Далее для нахождения расстояния d=АС применяется теорема синусов, из которой следует АС/sinВ=АВ/sinС. Подставляя вместо неизвестных полученные из теоремы выражения, получаем d=с sinβ/sin(α+β). Также отмечается, что аналогично данному ходу решения определяются расстояния до небесных светил.

Видеоурок «Измерительные работы» может быть использован в ходе традиционного урока геометрии вместо объяснения учителя. Также данный материал можно рекомендовать ученикам для самостоятельного рассмотрения. Поможет данное наглядное пособие учителю представить практическое значение изученного материала и в ходе дистанционного обучения.
| Автор | |
|---|---|
| Дата добавления | 02.08.2014 |
| Раздел | Геометрия |
| Подраздел | Видеоурок |
| Просмотров | 4923 |
| Номер материала | 761 |