
Урок «Неравенства с модулем»

Краткое описание документа:
В математике очень распространены неравенства, содержащие переменную под знаком модуля.
На этом уроке мы рассмотрим различные способы решения этих неравенств.
Для изучения этой темы вспомним определение модуля числа и его геометрический смысл.
Модулем числа называется само это число, если оно неотрицательное, или это же число с противоположным знаком, если оно отрицательное.
Геометрически модуль а означает расстояние на координатной прямой от начала отсчета до точки, изображающей число а.
Если а не равно нулю, то на координатной прямой существуют две точки а и минус а, равноудаленные от нуля, модули которых равны.
Первый способ (геометрический смысл модуля). Рассмотрим на простых примерах.
Задание 1
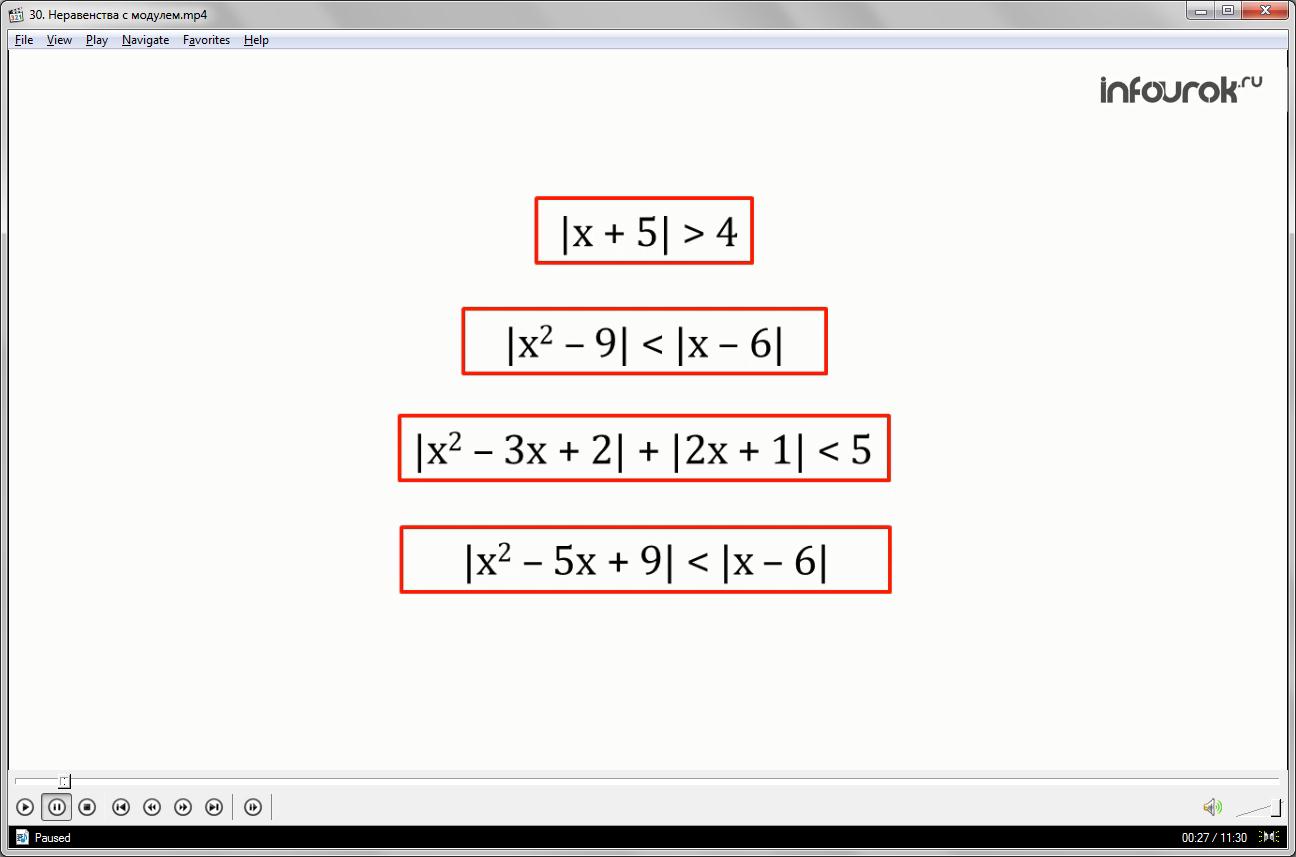
Решить неравенство модуль икс минус трех меньше четырех.
Решение
Рисуем координатную прямую.
Модуль икс минус трех меньше четырех означает, что расстояние от точки икс до точки три меньше четырех единиц. Отмечаем на прямой число три и отсчитываем влево и вправо от него четыре деления. Слева мы придем к точке один, справа – к точке семь. Таким образом, границы точки икс мы просто увидели, не вычисляя их.
При этом, согласно условию неравенства, сами минус один и семь не включены во множество решений. Таким образом, ответ:
интервал от минус единицы до семи.
Второй способ – графическое решение.
Задание 2
Решить неравенство икс минус один меньше модуля квадрата разности икс и двух и минус один.
Решение
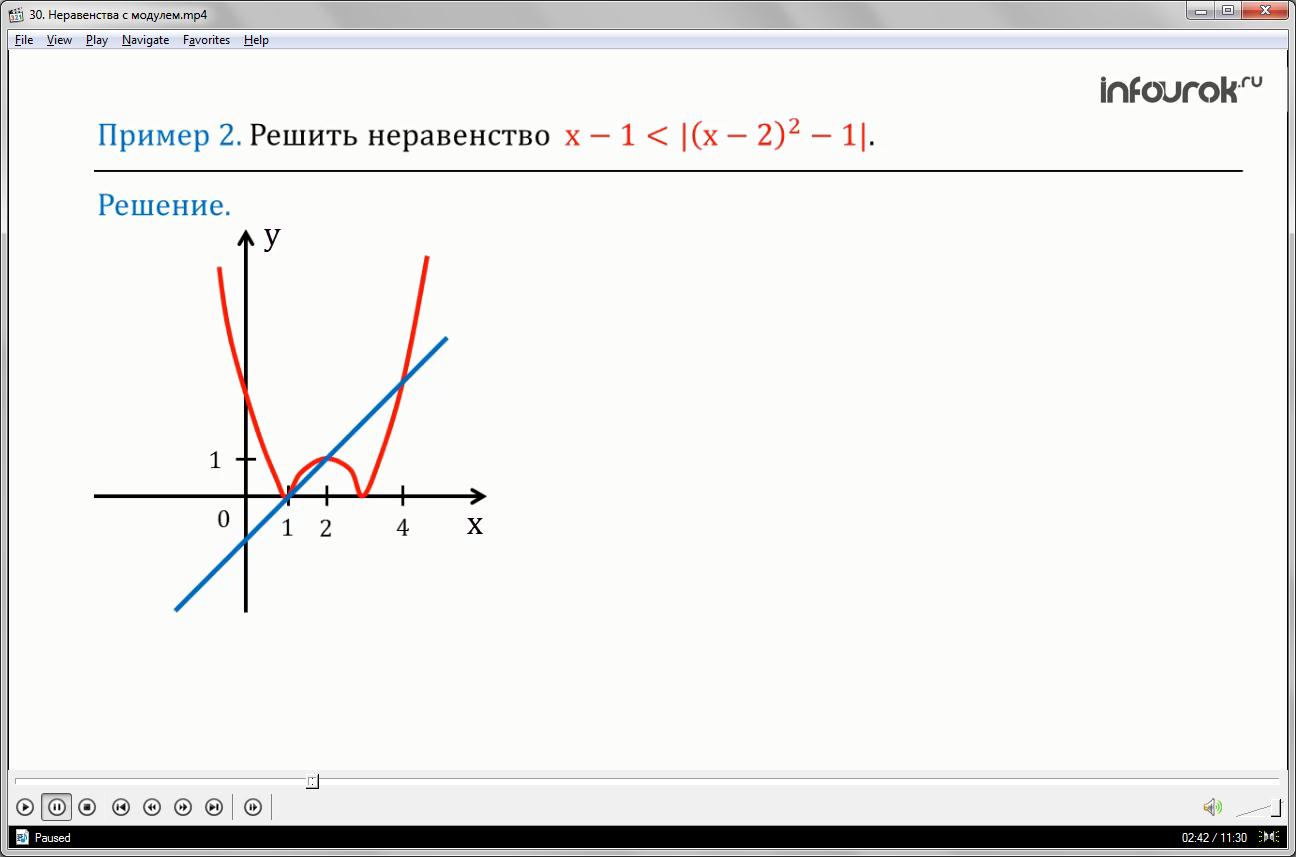
Построим в одной системе координат графики функций: игрек равен икс минус один и игрек равен модуль икс минус два и все в квадрате и минус один.
Графиком линейной функции игрек равен икс минус один является прямая, проходящая через точки, например, с координатами один и ноль и четыре и ноль. График функции игрек равен модуль икс минус два и все квадрате и минус один. Используя алгоритм, делаем построения графика функции игрек равен модуль эф от икс.
Находим точки пересечения графиков. В ответе указываем те значения икс, при которых график первой функции расположен ниже графика второй функции.
Этообъединение открытого числового луча от минус бесконечности до единицы, интервала от одного до двух и открытого числового луча от четырех до плюс бесконечности.
Ответ: объединение открытого числового луча от минус бесконечности до единицы, интервала от одного до двух и открытого числового луча от четырех до плюс бесконечности.
Третий способ – возведение в квадрат.
Задание 3
Решить неравенство модуль икс квадрат минус один меньше модуля икс квадрат минус икс плюс один.
Решение
Возведем обе части неравенства в квадрат. Заметим, что возводить обе части неравенства в квадрат можно только в том случае, когда они обе положительные. В данном случае у нас и слева, и справа стоят модули, поэтому мы можем это сделать.
Теперь воспользуемся следующим свойством модуля: квадрат модуля икс равен икс квадрат. Получим икс квадрат минус один и все в квадрате минус икс квадрат минус икс плюс один и все в квадрате меньше нуля.
Дальше лучше всего воспользоваться формулой разности квадратов. Можно, конечно, и возводить в квадрат левую и правую скобку, но это займет гораздо больше времени. Имеем произведение трех множителей меньше нуля.
Решаем методом интервалов.
Из рисунка видно, что
решением неравенства является объединение открытого числового луча от минус бесконечности до нуля и интервала от одной второй до двух.
Ответ: объединение открытого числового луча от минус бесконечности до нуля и интервала от одной второй до двух.
Четвертый способ (определение модуля).
Задание 4
Решить неравенство три умноженное на модуль икс минус один меньше либо равно икс плюс три.
Решение
По определению модуля выражение икс минус один может быть неотрицательным или отрицательным.
Если икс минус один больше либо равно нулю, то заданное неравенство примет вид два икс больше либо равно шести.
Если икс минус один меньше нуля, то заданное неравенство примет вид минус четыре икс меньше либо равно нулю.
Таким образом, данное неравенство равносильно совокупности двух систем.
Решаем первую систему совокупности, получим, что решением является числовой отрезок от единицы до трех.
Решаем вторую систему совокупности, получим, что решением является числовой отрезок от нуля до единицы.
Решением данного неравенства является
объединение этих числовых отрезков, то есть числовой отрезок от нуля до трех.
Ответ: числовой отрезок от нуля до трех.
Четвертый способ является наиболее универсальным, но в зависимости от ситуации используются и остальные.
Задание 5
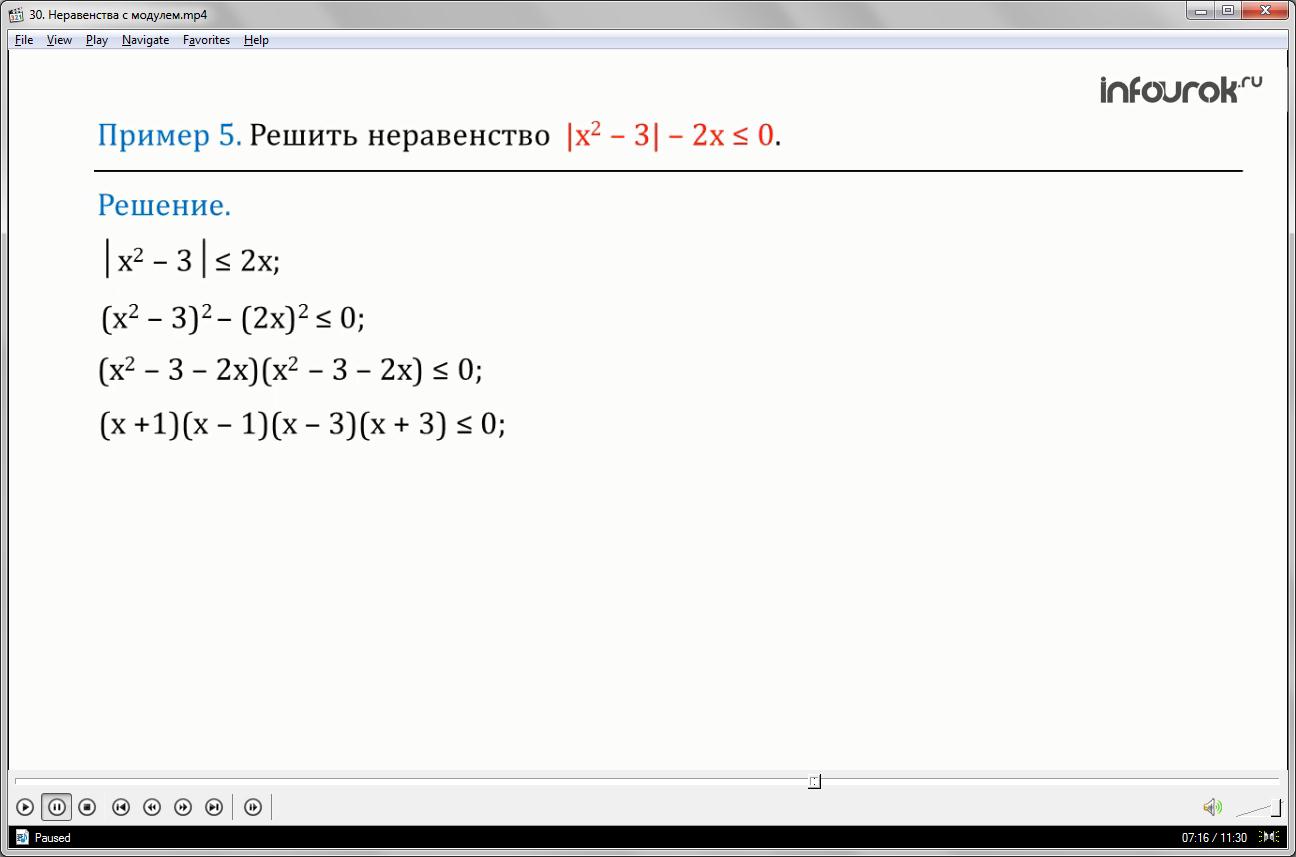
Решить неравенство модуль икс квадрат минус три минус два икс меньше либо равно нулю.
Решение
Преобразуем неравенство. Перенесем два икс в правую часть неравенства.
Замечаем, что левая часть неравенства неотрицательна, значит, и правая часть должна быть неотрицательной, то есть икс больше либо равно нулю. Так как обе части неравенства неотрицательны, то их можно возвести в квадрат (третий способ) и разложить на множители по формуле разности квадратов. Получаем произведение четырех множителей меньше либо равно нулю.
Решим это неравенство методом интервалов. Из рисунка видно, что решение этого неравенства — объединение числовых отрезков от минус трех до минус единицы и от единицы до трех.
Учитывая условие икс больше либо равно нулю, получим решение исходного неравенства — отрезок от одного до трех.
Ответ: отрезок от одного до трех.
Задание 6
Решить неравенство модуль икс минус четыре больше модуля икс плюс шесть.
Решение
Обе части данного неравенства неотрицательны для любых значений икс, поэтому их можно возвести в квадрат, затем
разложить на множители по формуле разности квадратов, привести подобные члены, разделить на минус десять. Получим неравенство икс меньше минус одного.
Решением этого неравенства,а значит, иравносильного ему данного неравенства является открытый числовой луч от минус бесконечности до минус единицы.
Ответ: открытый числовой луч от минус бесконечности до минус единицы.
Задание 7
Решить неравенство икс минус один больше кубического корня из икс в кубе минус два икс в квадрате плюс четыре икс минус семь.
Решение
Возведя обе части этого неравенства в третью степень, получим неравенство,
равносильное данному.
Применив формулу куба разности, перенеся все члены неравенства в правую часть и приведя подобные члены многочлена,
получим квадратное неравенство икс в квадрате плюс икс минус шесть меньше нуля, равносильное данному неравенству.
Решением этого неравенства, а значит, иравносильного ему исходного неравенства является интервал от минус трех до двух. Ответ: интервал от минус трех до двух.
Задание 8
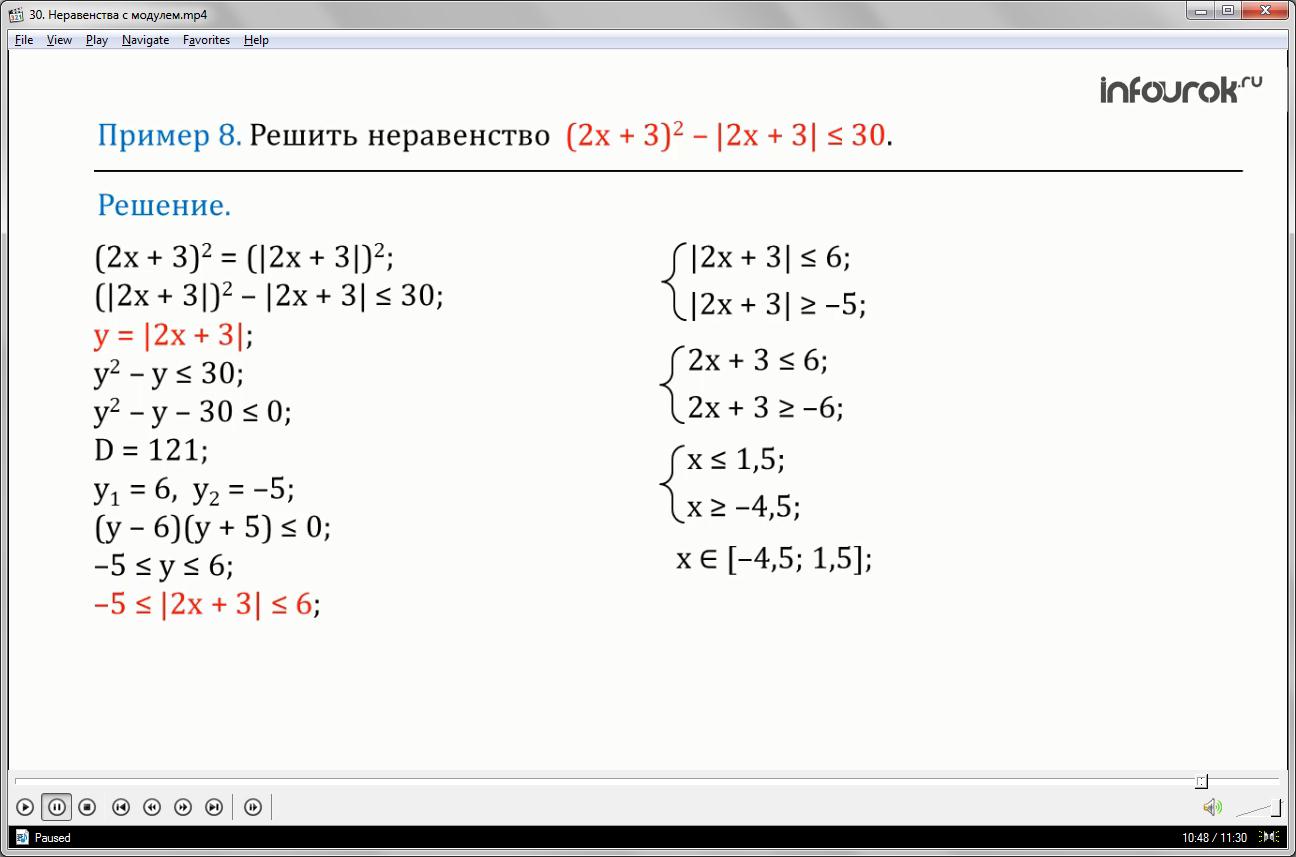
Решить неравенство два икс плюс три и все в квадрате минус модуль двух икс плюс три меньше либо равно тридцати.
Решение
Заметим, что два икс плюс три и все в квадрате равно квадрату модуля два икс плюс три. Тогда получим квадратное неравенство, в котором
сделаем замену: игрек равен модулю два икс плюс три.
Перепишем наше неравенство с учетом замены, разложим на множители и получим неравенство игрек минус шесть умноженное на игрек плюс пять меньше либо равно нулю.
Решим методом интервалов и получим:
игрек меньше либо равен минус пять и меньше либо равен шести.
Вернемся к замене, и данное двойное неравенство равносильно системе неравенств.
Решим первое неравенство из этой системы. Оно равносильно системе неравенств.
Два икс плюс три меньше либо равно шести и два икс плюс три больше либо равно минус шести.
Ее решением является отрезок от минус четырех целых пяти десятых до одной целой пяти десятых.
Второе неравенство системы — модуль двух икс плюс три больше либо равно минус пяти — очевидно выполняется для всех икс, так как модуль по определению число положительное. Так как решение системы неравенств – это все икс, которые удовлетворяют одновременно и первому и второму неравенству системы, то ее решением, а значит, и исходного неравенства, будет решение ее первого неравенства (ведь решением системы будет решение ее первого неравенства, то есть числовой отрезок от минус четырех целых пяти десятых до одной целой пяти десятых.
Ответ: числовой отрезок от минус четырех целых пяти десятых до одной целой пяти десятых.
| Автор | |
|---|---|
| Дата добавления | 16.11.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 10916 |
| Номер материала | 1079 |