
Урок "Окружность, вписанная в правильный многоугольник"

Краткое описание документа:
Видеоурок «Окружность, вписанная в правильный многоугольник» раскрывает содержание и описывает подробное доказательство теоремы об окружности, вписанной в правильный многоугольник, а также представляет ученикам важные следствия из данной теоремы. Основная задача данного видеоурока – облегчить усвоение учениками учебного материала по данной теме. Видеоурок учитель может использовать как наглядное пособие для сопровождения своего объяснения. Также данный видеоматериал может служить отдельной частью урока, полностью заменяя объяснение учителя и освобождая его для усиления индивидуальной работы с учениками. Это дает возможность сэкономить время урока, повысить эффективность обучения.
В ходе видеоурока используются анимационные эффекты, которые делают построения приближенными к традиционным иллюстрациям на доске при помощи мела и линейки. Однако на экране сделанные построения более четкие, хорошо видны ученикам с любого места в классе. При этом важные детали построения отмечены цветом, помогая ученику отметить важные особенности построения. Формулировки определений и теорем выделены цветом, дополнительно озвучиваются диктором. Это способствует лучшему запоминанию материала еще в классе при объяснении темы.
Видеоурок начинается с представления темы. Ученикам напоминается определение окружности, которая вписана в многоугольник. Представляется формулировка данной окружности как окружности, которой касаются все его стороны. Далее рассматривается доказательство теоремы о том, что возможно вписание в произвольный правильный многоугольник окружности, при этом такая окружность только одна. На экран выводится данное утверждение и озвучивается диктором.
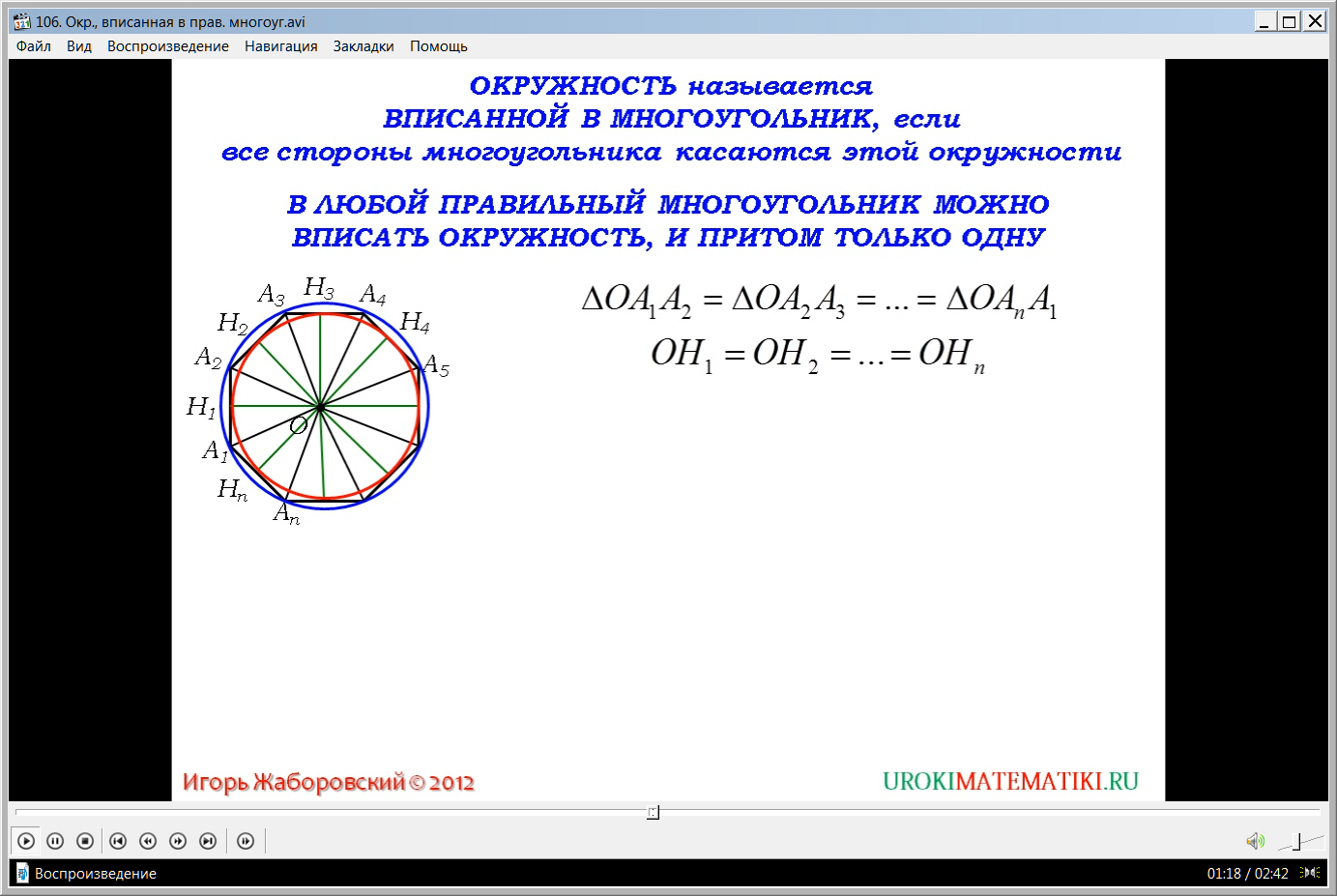
Доказательство теоремы начинается с рисунка правильного n-угольника. Демонстрируется многоугольник и построенная около него описанная окружность. Отмечается, что доказательство данной теоремы использует данные, которые уже были доказаны в ходе рассуждений при доказательстве теоремы об окружности, что описана около многоугольника. Действительно, было доказано, что образованные биссектрисами углов треугольники равны ΔОА1А2= ΔОА2А3=…= ΔОАnА1. Из равенства эти х треугольников следует равенство их высот, опущенных из вершины О, то есть ОН1=ОН2=…=ОНn. Это означает, что можно построить окружность, вписанную в n-угольник, которая касается точек пересечения высоты треугольника и его основания. Очевидно, данная окружность будет вписанной в многоугольник.
Вторая часть доказательства посвящена рассуждениям о том, является ли построенная вписанная окружность единственной. Доказательство выполняется от противного. Предполагается, что существует еще одна вписанная окружность. Это также означает, что существует еще одна равноудаленная от сторон n-угольника точка О1,. При этом она будет лежать на каждой биссектрисе этого многоугольника. Очевидно, что она совпадает с точкой О, в которой пересекаются биссектрисы. Радиус новой окружности будет равен расстоянию, измеренному до сторон многоугольника, то есть его длина ОН1. Из этого следует, что окружности совпадут. Теорема полностью доказана.

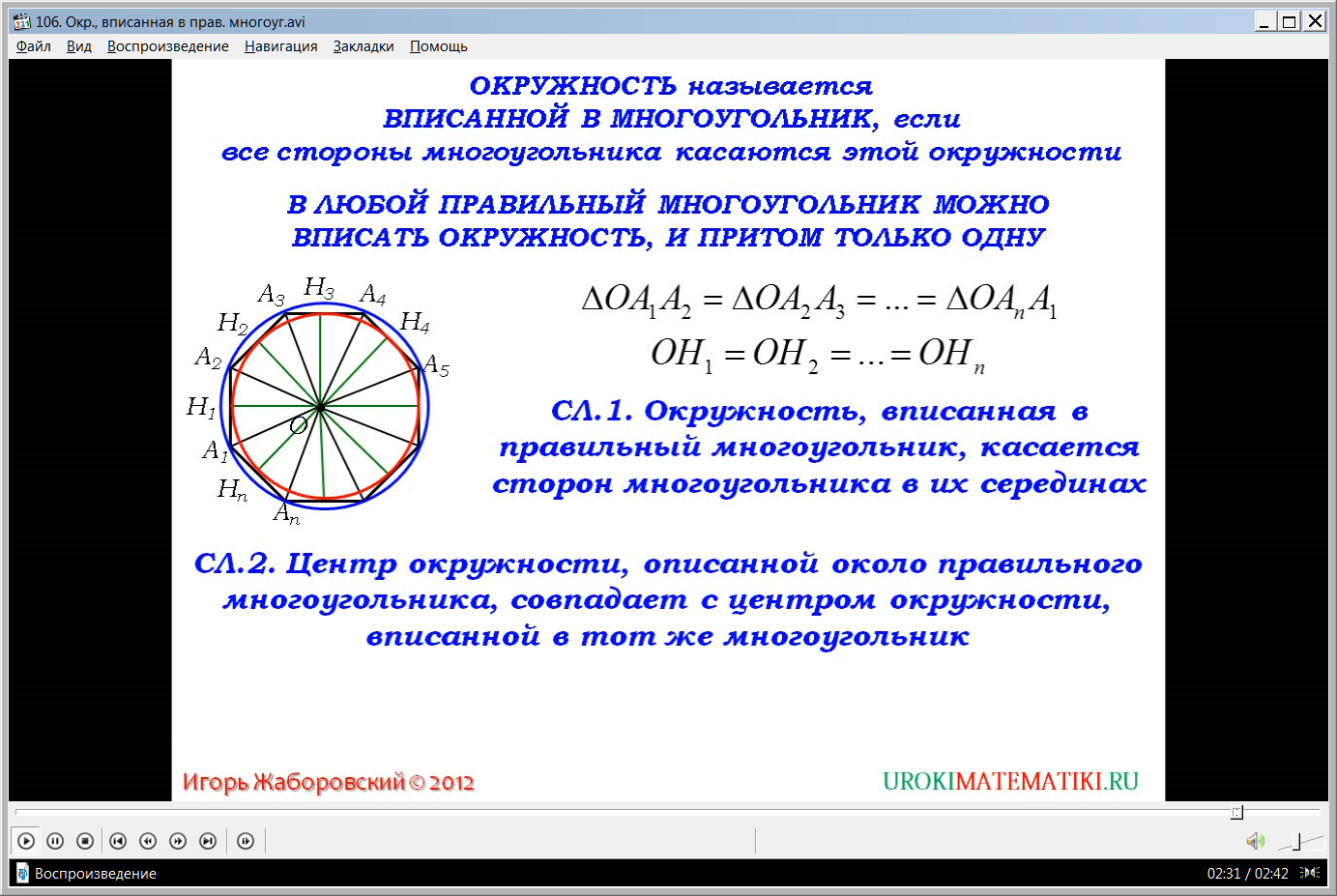
В конце видеоурока рассматриваются следствия из теоремы о вписанной окружности. Первое следствие утверждает, что точки касания вписанной окружности сторон многоугольника, являются серединами сторон. Во втором следствии отмечается, что центры окружностей – и вписанной, и описанной около данного правильного многоугольника, совпадают. Формулировки следствий выведены на экран, выделены цветом и озвучены диктором. Отмечается также, что указанный в следствии центр окружностей называется центром правильного многоугольника.
Видеоурок «Окружность, вписанная в правильный многоугольник» рекомендуется в качестве пособия для учителя при ведении традиционных уроков в школе по данной теме. Также видеоматериал поможет достичь учебных целей учителю, осуществляющему дистанционное обучение. Видео поможет разобраться с доказательством теоремы ученикам, которые самостоятельно осваивают курс математики, а также тем, кто требует дополнительного средства обучения для более глубокого понимания.
| Автор | |
|---|---|
| Дата добавления | 02.08.2014 |
| Раздел | Геометрия |
| Подраздел | Видеоурок |
| Просмотров | 5758 |
| Номер материала | 754 |