
Урок "Признаки делимости на 10, на 5 и на 2"

Краткое описание документа:
Видеоурок «Признаки делимости на 10, на 5 и на 2» раскрывает тему подробным образом на простых и понятных примерах. Голос диктора, сопровождающий урок, является спокойным.
Структура урока последовательна. Каждое утверждение сопровождается примерами, для закрепления материала.
В первую очередь рассматривается деление чисел на 10. Если ученик пропустит это знание, то в дальнейшем он столкнется с большими трудностями при делении и умножении на 100, 1000 и т.п.
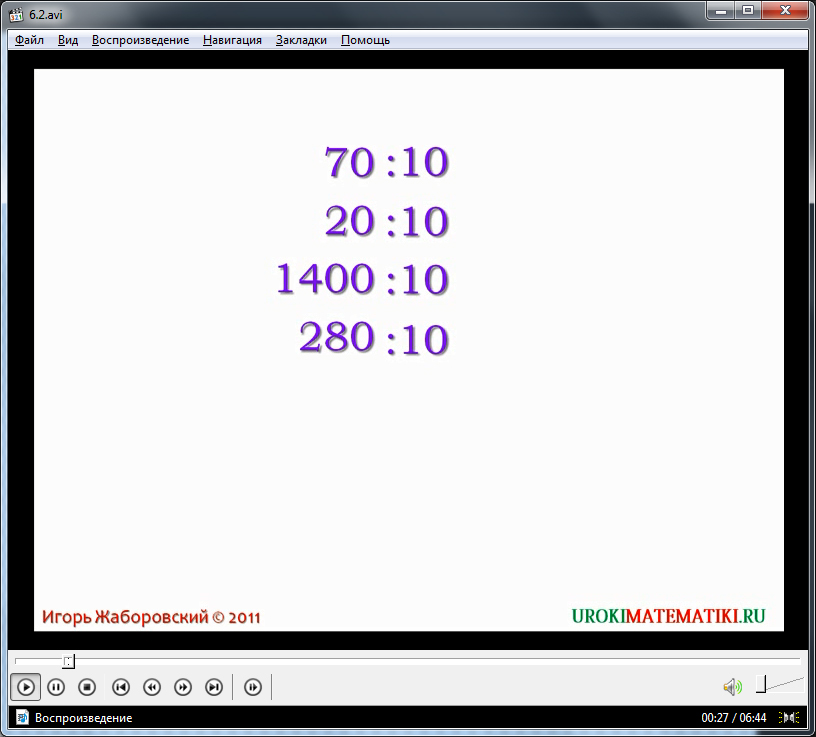
Диктор сообщает о том, что все натуральные числа, которые оканчиваются на 0, делятся без остатка на число 10. Подразумевается, что обучающийся по видеоуроку школьник уже ознакомлен с понятиями «натуральное число» и «деление без остатка».
Итак, чтобы поделить число, оканчивающееся на 0, необходимо отбросить последнюю цифру (т. е. - 0). После этого на экране выводится 5 примеров деления двух-, трех- и четырехзначных чисел на 10. Демонстрируется деление в виде анимации, в которой отсутствуют дополнительные отвлекающие эффекты.
Чтобы стало более понятно, рассматривается случай, при котором число (в примере - 283) не делится без остатка на 10. Результат выводится на экран, при котором явно виден остаток, сулящий о невозможности деления на 10.
На следующем шаге повторяется изученный материал для лучшего его закрепления.
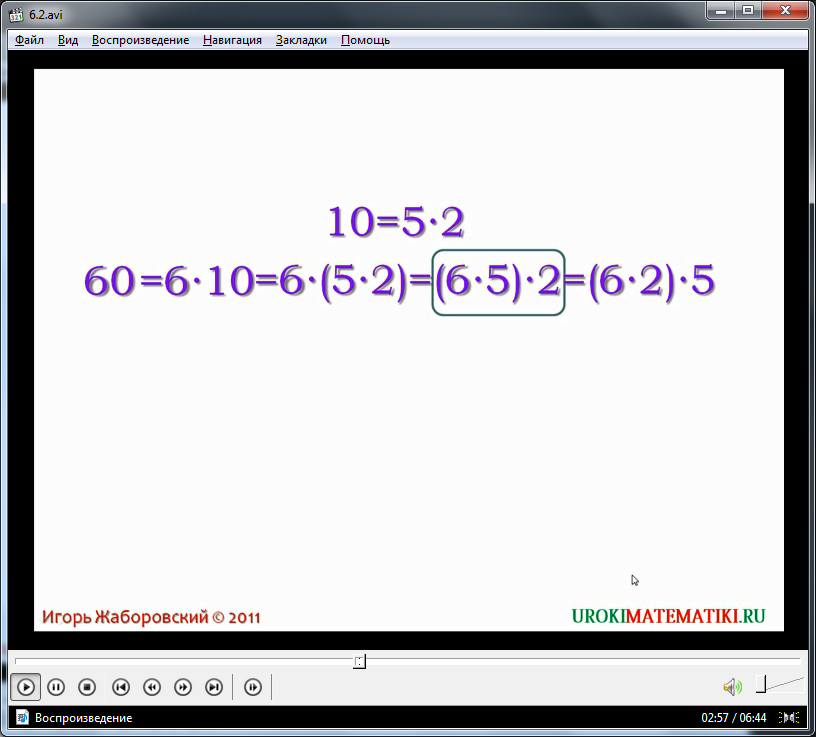
Прежде, чем перейти к дальнейшим объяснениям, а именно, к делению натуральных чисел без остатка на числа 5 и 2, в видеоуроке вводится некоторое предисловие, - число 10 можно представить в виде произведения 2 и 5. После чего диктор сообщает о том, что любое число, оканчивающееся на ноль, делится на эти числа без остатка. Чтобы не было никаких недоразумений, приводится объяснение данному утверждению. Дело в том, что любое число, оканчивающееся на 0, т. е. делящееся на 10 без остатка, можно представить в виде произведения, одним из множителей которого является, непосредственно, 10. А последнее, в свою очередь, представляется, как уже было сказано выше, в виде произведения натуральных чисел 5 и 2.
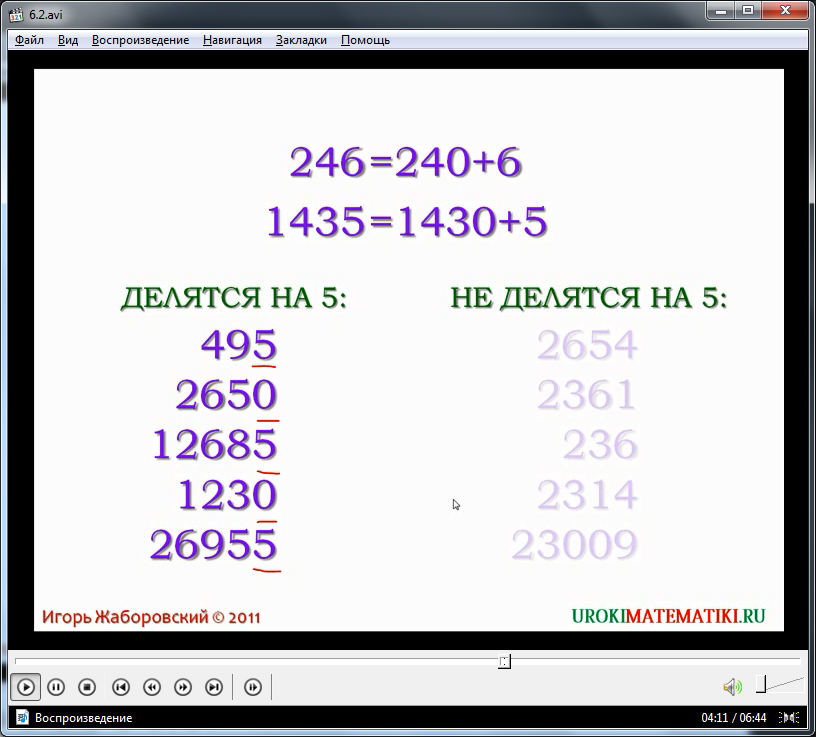
Далее демонстрируются примеры деления с остатком – противный случай. После этого выводится утверждение, в котором подробно говориться о том, какие именно числа делятся на число 5, – числа, заканчивающиеся на 5 и на 0.
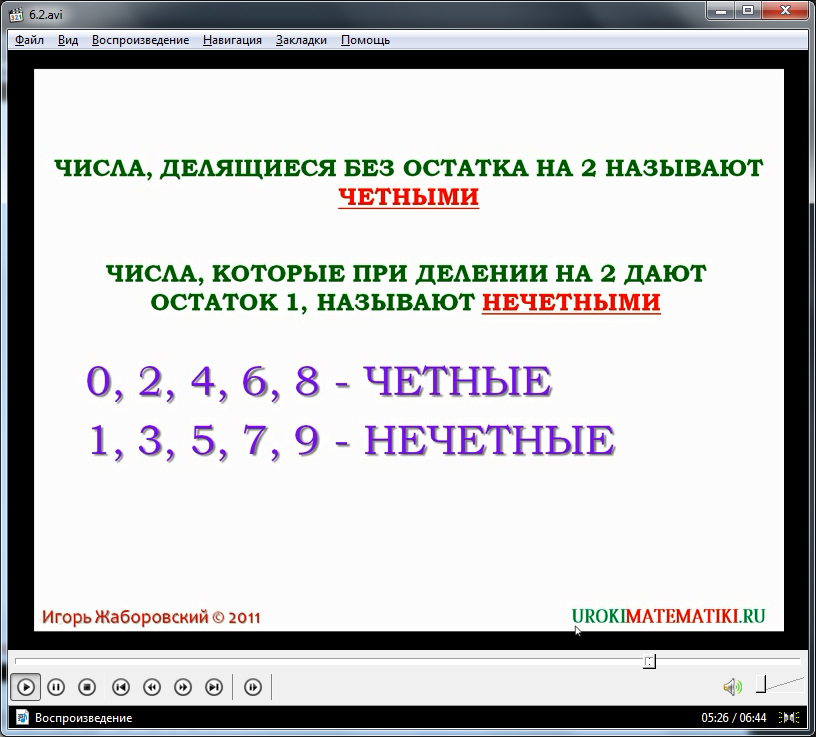
На следующем шаге, на примере деления чисел без остатка на 2, диктор объясняет принцип классификации натуральных чисел на четные и нечетные. Приводится пример, в котором демонстрируются однозначные числа, делящиеся на 2 (четные) и не делящиеся на 2 (нечетные).
После объяснения принципа подобной классификации натуральных чисел, на экран выводится утверждение, гласящее общее правило, согласно которому можно определить делимость на 2 без остатка. В тексте используются уже рассмотренные ранее понятия о четности и нечетности. Традиционно, приводятся примеры.
На завершительном этапе на экран выводятся вопросы, озвученные параллельно диктором, для самоконтроля, на которые обучающийся должен ответить с легкостью, в случае полного освоения материала. В противном случае, ему стоит пересмотреть видеоурок и попытаться решить примеры, без подсказок.
Стоит отметить, что текст, который сопровождает урок, выводится на белом фоне без узоров и ненужных иллюстраций, легко читается и воспринимается. Основные слова выделены красным цветом, что помогает лучше зрительно запоминать и акцентировать внимание на определенные понятия и выражения.
Видеоурок «Признаки делимости на 10, на 5 и на 2» может быть использован для самостоятельного домашнего обучения, либо учителем информатики при составлении конспекта урока.
| Автор | |
|---|---|
| Дата добавления | 25.07.2014 |
| Раздел | Математика |
| Подраздел | Видеоурок |
| Просмотров | 4535 |
| Номер материала | 439 |