
Урок «Равносильность уравнений»

Краткое описание документа:
Начиная с 7 класса, мы постоянно решаем различные типы уравнений с одной переменной, системы уравнений с двумя переменными. И в 11 классе мы вновь обращаемся к этой теме, чтобы рассмотреть ее с самых общих позиций.
Определение первое.Два уравнения с одной переменной эф от икс равно же от икси
пэ от икс равно аш от икс
называют равносильными, если множество их корней совпадают.
Задание 1
Выяснить, являются ли уравнения икс квадрат минус один равно нулю и икс минус один равно нулю равносильными?
Решение
Вычислим корни уравнения икс квадрат минус один равно нулю. Оно имеет два корня: икс первое равно единице, икс второе равно минус единице.
Вычислим корни уравнения икс минус один равно нулю. Это уравнение имеет один корень — икс равен единице.
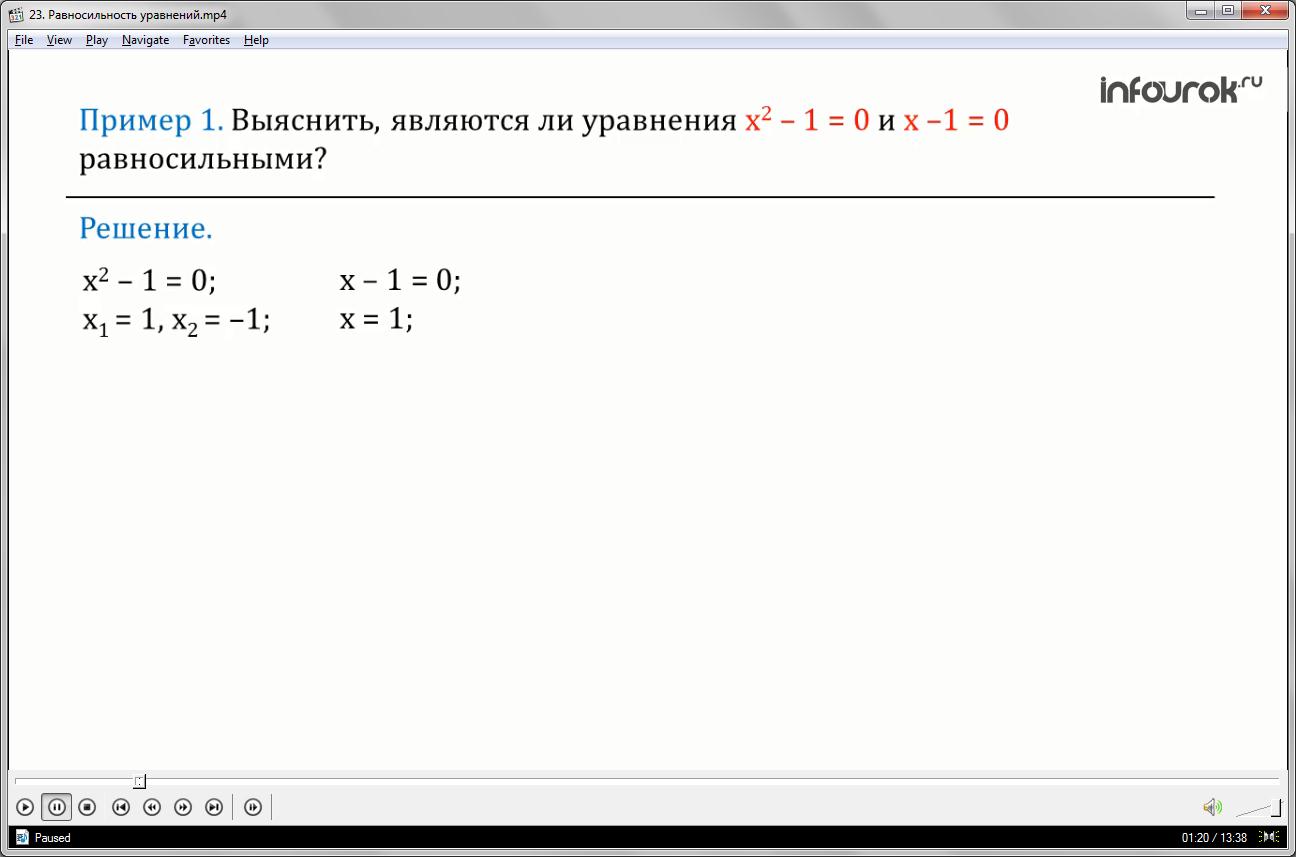
Данные уравнения не являются равносильными, т.к. уравнение икс квадрат минус один равно нулю имеет два корня, а уравнение икс минус один равно нулю
имеет один корень — икс равен единице.
Задание 2
Выяснить, являются ли уравнения икс квадрат минус девять равно нулю и произведение икс плюс три и два в степени икс минус восемь равно нулю равносильными?
Решение
Данные уравнения являются равносильными, так как каждое из них имеет по два корня: икс первое равно трем, икс второе равно минус трем.
Задание 3
Выяснить, являются ли уравнения икс квадрат плюс три равно нулю и квадратный корень из икс плюс пять равно нулю равносильными?
Решение
Данные уравнения являются равносильными, так как каждое из них не имеет корней.
Итак, сделаем вывод.
Если два уравнения имеют одинаковые корни или не имеют корней, то такие уравнения равносильные.
Определение второе.
Если каждый корень уравнения эф от икс равно же от икс (обозначим его номером один) является в то же время корнем уравнения пэ от икс равно аш от икс (обозначим его номером два), то второе уравнение называют следствием уравнения первого.
Задание 4
Выяснить, какое из уравнений: икс минус два равно нулю и икс квадрат минус пять икс плюс шесть равно нулю, является следствием другого.
Решение
Обозначим уравнение икс минус два равно нулю номером один, а уравнение икс квадрат минус пять икс плюс шесть равно нулю номером два.
Уравнение первое имеет единственный корень, равный двум.
Уравнение второе имеет два корня: икс первое равно двум, икс второе равно трем.
Единственный корень первого уравнения — икс равен двум — является также корнем второго. Поэтому второе является следствием первого уравнения.
Задание 5
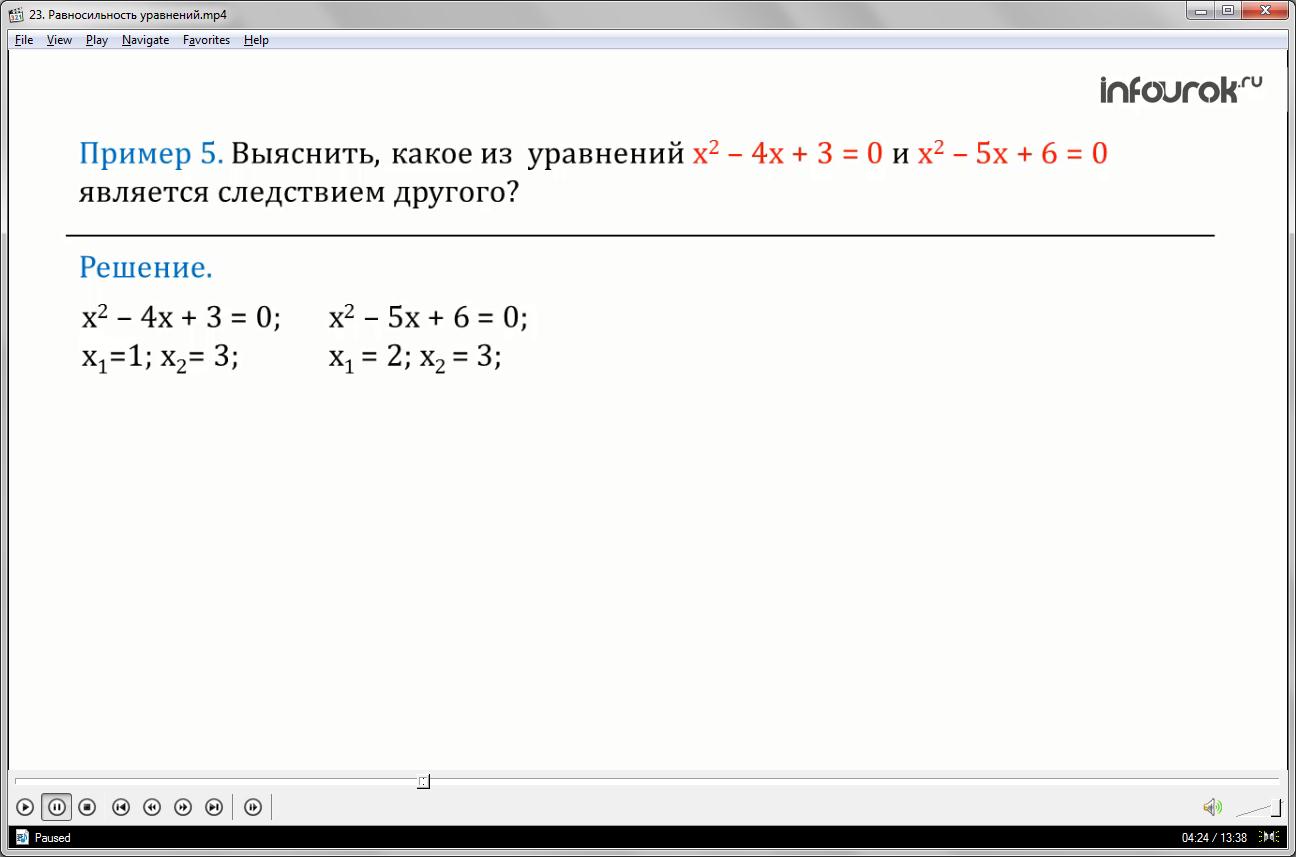
Выяснить, какое из уравнений — икс квадрат минус четыре икс плюс три равно нулю и икс квадрат минус пять икс плюс шесть равно нулю — является следствием другого.
Решение
Обозначим уравнение икс квадрат минус четыре икс плюс три равно нулю номером один, а уравнение икс квадрат минус пять икс плюс шесть равно нулю — номером два Уравнение первое имеет два корня: икс первое равно единице, икс второе равно трем.
Уравнение второе имеет два корня: икс первое равно двум, икс второе равно трем.
Оба уравнения имеют только по одному общему корню. Согласно определению, ни одно из них не является следствием другого.
Запомни!Если каждое из двух уравнений является следствием другого, то такие два уравнения равносильны.
А теперь изучим, из каких этапов состоит решение уравнения.
Решение любых уравнений происходит в три этапа:
Первый этап — технический. С помощью цепочки преобразований от исходного уравнения мы приходим к достаточно простому уравнению, которое решаем и находим корни.
Второй этап — анализ решения. Анализируем преобразования, которые выполнили, и выясняем, равносильны ли они.
Третий этап — проверка. Проверка всех найденных корней их подстановкой в исходное уравнение обязательна при выполнении преобразований, которые могут привести к уравнению-следствию.
Чтобы выполнить второй этап, нам нужно знать ответ на вопрос, какие преобразования приводят к равносильному уравнению?
Обычно при решении уравнений используются шесть теорем равносильности.
Теорема первая. Если какой-либо член уравнения перенести из одной части уравнения в другую с противоположным знаком, то получится уравнение, равносильное данному уравнению.
Например, если в уравнении икс в пятой степени плюс три икс в квадрате минус семь равно четырем икс плюс десять перенести слагаемые четыре икс и минус семь из одной части в другую, то получим уравнение, равносильное данному уравнению.
Теорема вторая. Если обе части уравнения возвести в одну и ту же нечетную степень, то получится уравнение, равносильное данному уравнению.
Например, уравнения корень пятой степени из икс в квадрате минус два икс минус три равно двум и икс квадрат минус два икс минус три равно тридцати двум после возведения обеих частей уравнения в пятую степень, в силу теоремы второй, равносильны.
Теорема третья. Показательное уравнение а в степени эф от икс равно а в степени жэ от икс, где а больше нуля и а не равно единице равносильно уравнению эф от икс равно жэ от икс.
Например, показательное уравнение четыре в степени квадратный корень из трех икс минус два равно четыре в степени два икс плюс один равносильно уравнению
квадратный корень из трех икс минус два равно двум икс плюс один.
Эти три теоремы называются «спокойными». Их применение гарантирует равносильность преобразований без дополнительных условий. Обычно их использование происходит автоматически, без особых размышлений.
Следующие три теоремы называются «беспокойными». Их применение возможно при выполнении определенных условий.
При их применении требуются внимание и аккуратность.
Определение третье.Областью определения уравнения эф от икс равно же от икс,или областью допустимых значений переменной (сокращенно ОДЗ) называют множество тех значений переменной икс, при которых одновременно имеют смысл выражения: эф от икси же от икс.
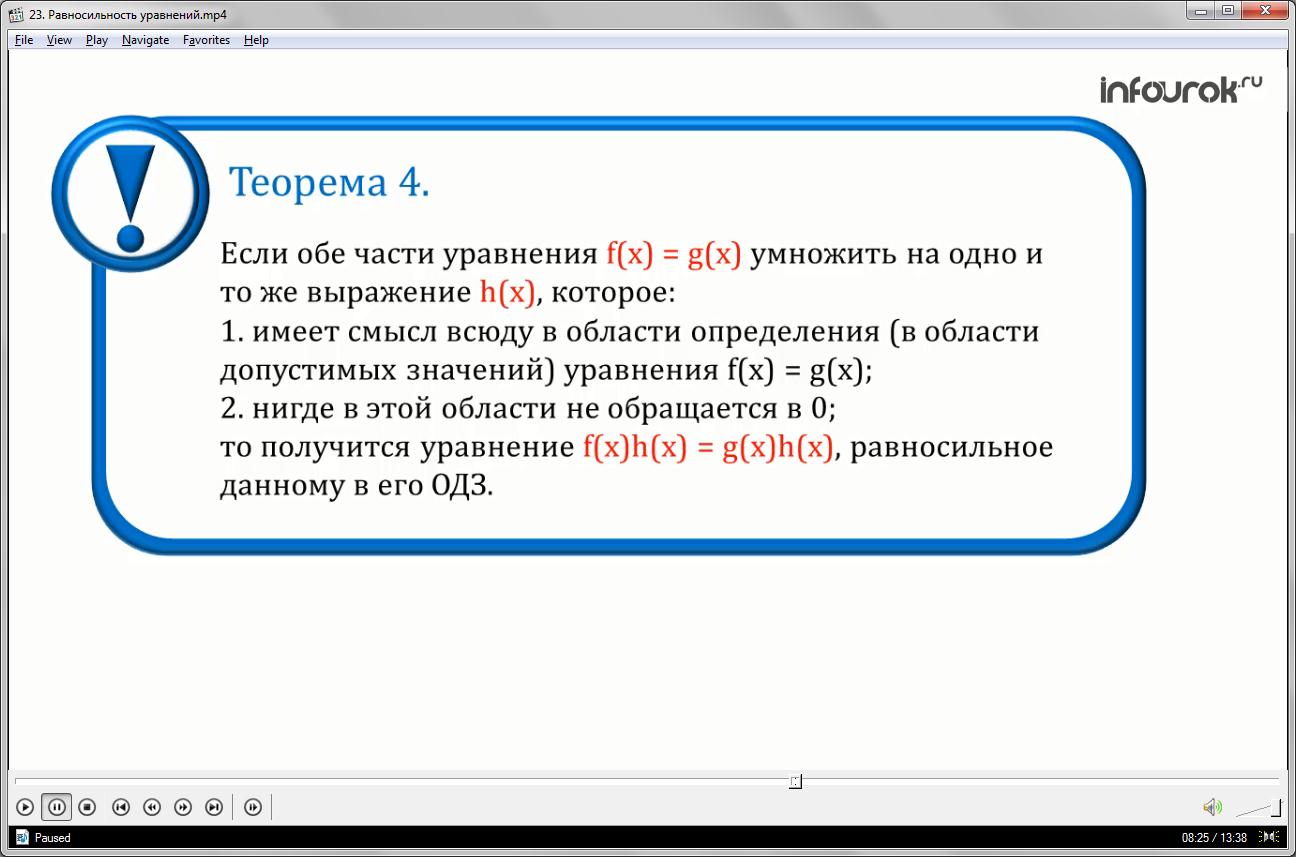
Теорема четвертая. Если обе части уравнения эф от икс равно же от иксумножить на одно и то же выражение аш от икс, которое:
Во-первых, имеет смысл всюду в области определения (в области допустимых значений) уравнения эф от икс равно же от икс.
Во-вторых, нигде в этой области не обращается в нуль, то получится уравнение эф от икс, умноженное на аш от икс, равно же от икс, умноженное на аш от икс, равносильное данному в его ОДЗ.
Следствием теоремы четыре является еще одно «спокойное» утверждение: если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получится уравнение, равносильное данному.
Задание 6
Выяснить, будет ли уравнение: дробь, числитель которой квадратный корень из двух икс минус один, а знаменатель икс плюс три равно дроби, числитель которой два икс минус семь, а знаменатель икс плюс три и уравнение квадратный корень из двух икс минус один равное двум икс минус семь равносильны?
Решение
ОДЗ первого уравнения задается условиями два икс минус один больше, либо равно единице и икс плюс три не равно нулю. Получаем — икс больше, либо равно нулю целым пяти десятым.
Выражение аш от икс равно икс плюс три в этой области имеет смысл и нигде не обращается в нуль. Поэтому обе части этого уравнения умножим на икс плюс три.
Согласно теореме четвертой, уравнение квадратный корень из двух икс минус один равное двум икс минус семь равносильно уравнению: дробь, числитель которой — квадратный корень из двух икс минус один, а знаменатель — икс плюс три, равная дроби, числитель которой — два икс минус семь, а знаменатель — икс плюс три (после умножения на выражение аш от икс равно икс плюс два).
Теорема пятая. Если обе части уравнения
эф от икс равно же от икснеотрицательны в о дэ зэ уравнения, то после возведения обеих его частей в одну и ту же четную степень n получится уравнение эф от икс в энной степени равно же от иксв энной степени равносильное данному уравнению в его о дэ зэ.
Задание 7
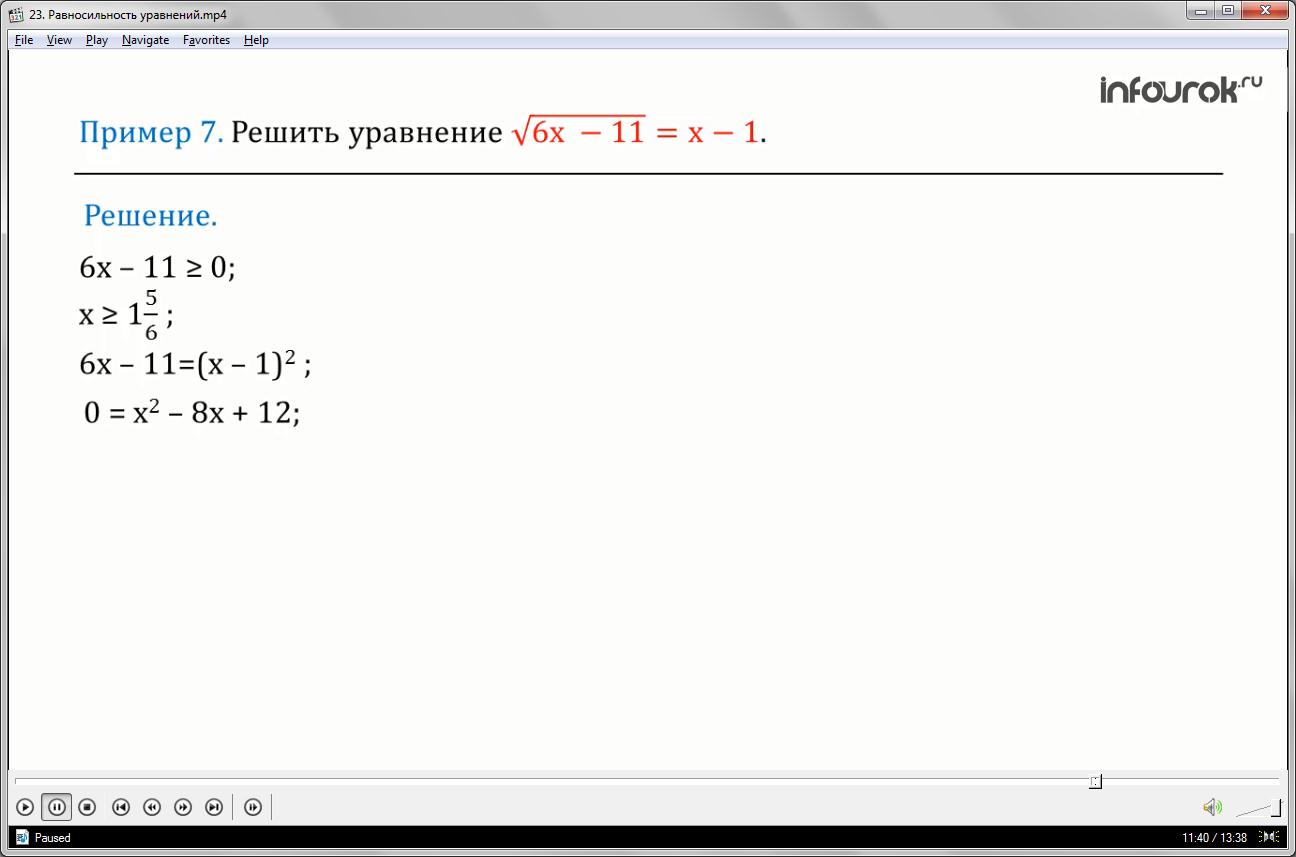
Решить уравнение: квадратный корень из шести икс минус одиннадцать равен икс минус один.
Решение
ОДЗ иррационального уравнения задается неравенством шесть икс минус одиннадцать больше, либо равно нулю, решение которого икс больше, либо равно одной целой пяти шестым.
В этой ОДЗ обе части уравнения неотрицательны. Возведем в квадрат обе части уравнения и получим, согласно теореме пятой, равносильное квадратное уравнение:
ноль равен икс в квадрате минус восемь икс плюс двенадцать. Корни которого икс первое равно шести и икс второе равно двум также будут корнями исходного уравнения.
Теорема шестая. Пусть а больше нуля , а не равно одному и эф от икс больше нуля,
жэ от икс больше нуля,тологарифмическое уравнение логарифм эф от икс по основанию а равно логарифму жэ от икс по основанию а
равносильно уравнению эф от икс равно же от икс.
Задание 8
Решить уравнение логарифм выражения три икс квадрат плюс два по основанию семь равно логарифму выражения четыре модуль икс плюс один по основанию семь.
Решение
В данном логарифмическом уравнении функции эф от икс равна три икс квадрат плюс два и жэ от икс равно четыре модуль икс плюс один принимают положительные значения при всех значениях переменной икс. По теореме шесть, данное уравнение равносильно уравнению три икс квадрат плюс два равно четырем модуля икс плюс один. Корни икс первое, второе равно плюс-минус одному и икс третье, четвертое равно плюс-минус одна третья. Они являются корнями исходного уравнения.
Если нарушаются условия применимости теорем четыре — шесть, то получится уравнение-следствие. Какие же преобразования переводят данное уравнение в уравнение-следствие? Об этом мы узнаем на следующем уроке.
| Автор | |
|---|---|
| Дата добавления | 16.11.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 6060 |
| Номер материала | 1072 |