
Урок «Решение неравенств с одной переменной. Иррациональные неравенства»

Краткое описание документа:
Ранее мы рассматривали простейшие иррациональные неравенства.
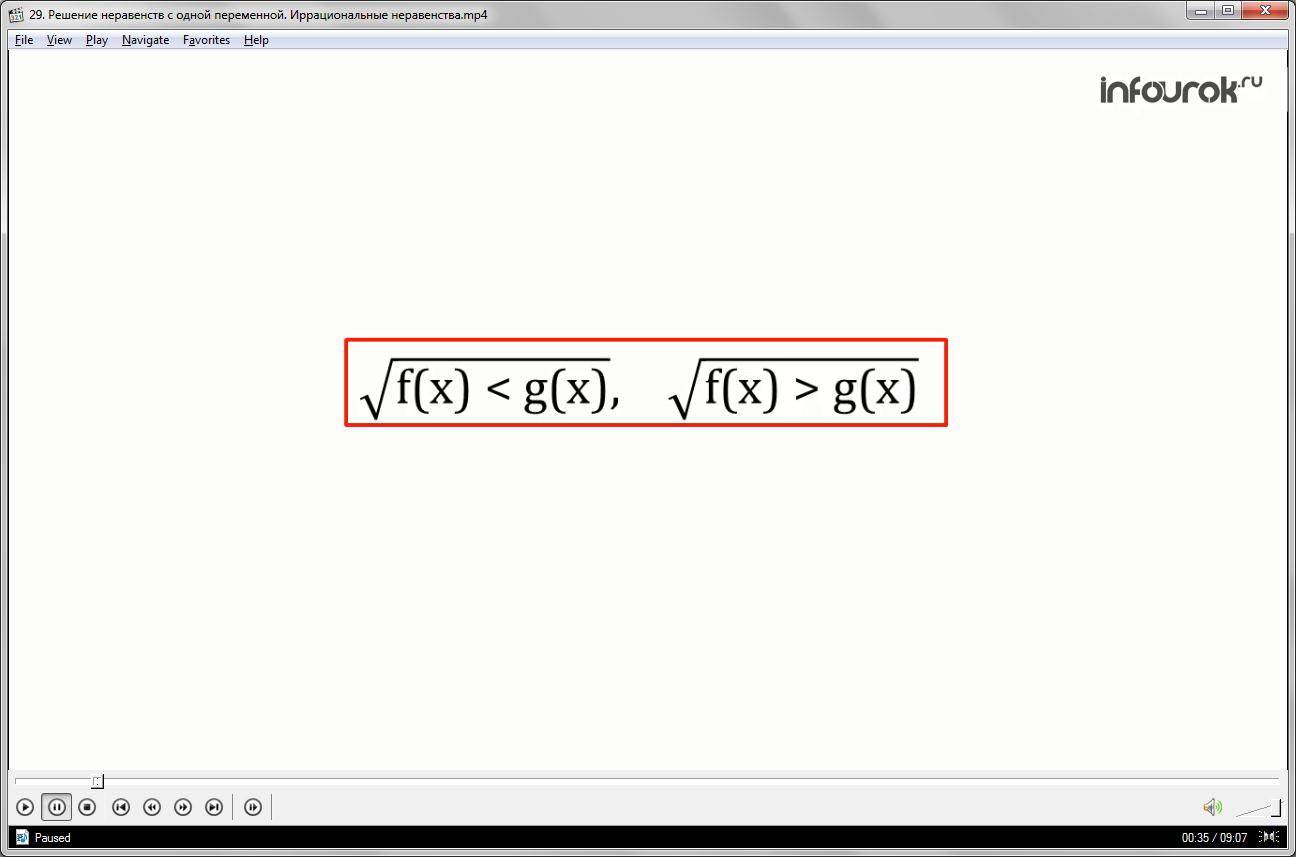
Сегодня на уроке мы рассмотрим решение более сложных неравенств вида квадратный корень из эф от икс меньше жэ от икс и квадратный корень из эф от икс больше жэ от икс.
Рассмотрим решение неравенства квадратный корень из эф от икс меньше жэ от икс. Обозначим его номером один.
Во-первых, ОДЗ неравенства задается условием эф от икс больше либо равно нулю.
Во-вторых, правая часть первого неравенства должна быть положительной, то есть жэ от икс больше нуля. При жэ от икс меньше либо равно нулю первое неравенство не имеет решения.
В-третьих, обе части первого неравенства неотрицательны, поэтому их можно возвести в квадрат (при этом знак неравенства сохраняется): эф от икс меньше жэ в квадрате от икс.
Таким образом, данное иррациональное неравенство равносильно системе неравенств:
эф от икс больше либо равно нуля,
жэ от икс больше нуля.,
эф от икс меньше жэ в квадрате от икс.
Задание 1
Решить неравенство квадратный корень из икс плюс два меньше икс.
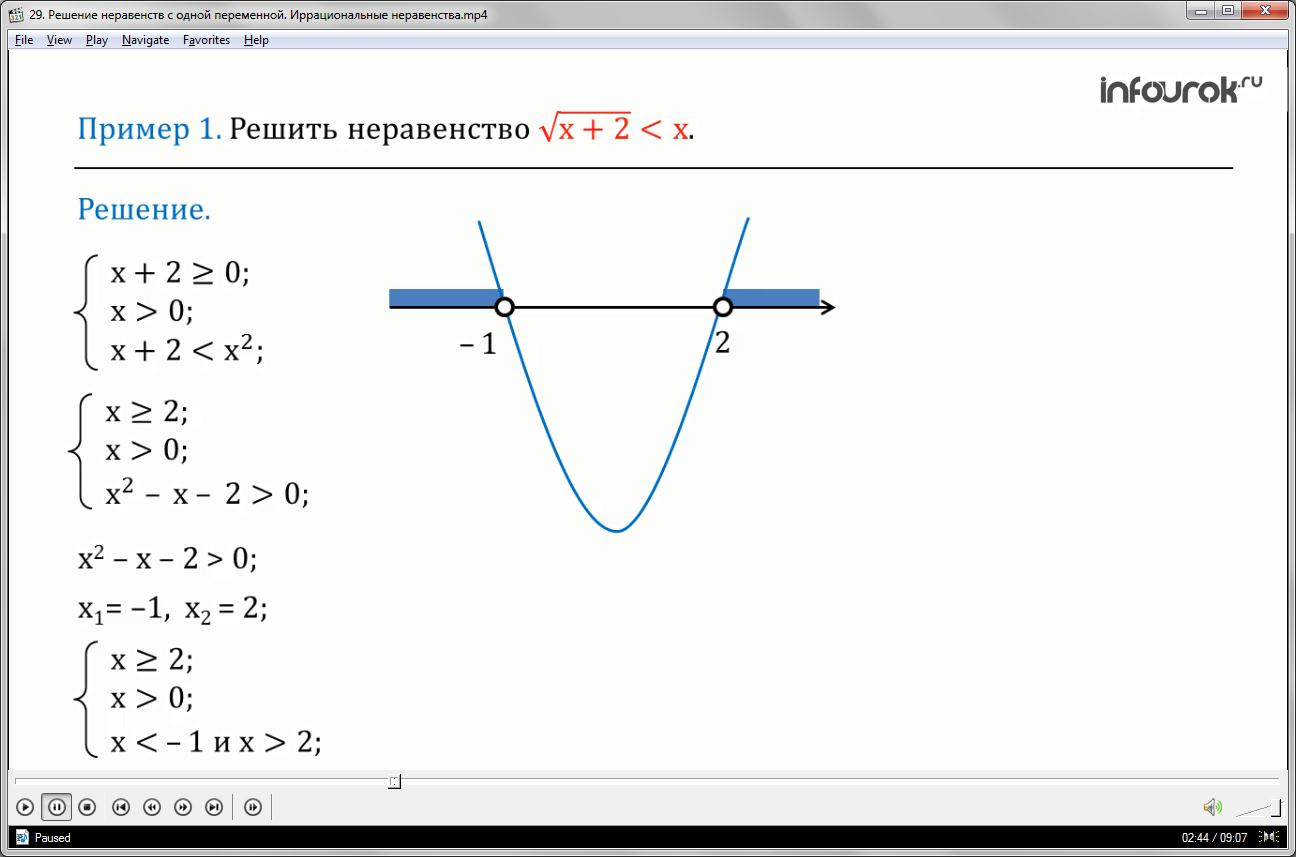
Это неравенство равносильно системе неравенств:
Икс плюс два больше либо равно нулю,
Икс больше нуля,
Икс плюс два меньше икс в квадрате.
Выполним преобразования в первом и третьем неравенствах — получим систему, в которой икс больше либо равно двум, икс больше нуля, икс квадрат минус икс минус два больше нуля.
Решим квадратное неравенство графически. Для этого найдем корни квадратного трехчлена икс квадрат минус икс минус два, получим икс первое равно минус единице, икс второе равно двум.
Геометрическая модель помогает найти решение неравенства: икс меньше минус одного и икс больше двух.
Имеем, систему неравенств:
икс больше либо равно двум,
икс больше нуля,
икс меньше минус одного и икс больше двух.
Тогда решение системы, а значит, и данного неравенства — открытый числовой луч от двух до плюс бесконечности.
Ответ:открытый числовой луч от двух до плюс бесконечности.
Задание 2
Решить неравенство квадратный корень из икс плюс восемнадцать меньше двух минус икс.
Это неравенство равносильно системе неравенств:
икс плюс восемнадцать больше либо равно нулю,
два минус икс больше нуля,
икс плюс восемнадцать меньше квадрата разности двух и икс.
Выполним преобразования в каждом неравенстве системы, получим систему, в которой икс больше либо равно минус восемнадцати, икс меньше двух, икс квадрат минус пять икс минус четырнадцать больше нуля.
Решим квадратное неравенство графическим способом. Для этого вычислим корни квадратного трехчлена
икс квадрат минус пять икс минус четырнадцать, получим икс первое равно минус двум, икс второе равно семи.
Геометрическая модель помогает найти решение неравенства: икс меньше минус двух и икс больше семи.
Итак, имеем систему неравенств:
икс больше либо равно минус восемнадцати, икс меньше двух,
икс меньше минус двух и
икс больше семи.
Тогда решением системы, а значит, и данного неравенства является полуинтервал от минус восемнадцати до минус двух, включая минус восемнадцать.
Ответ:полуинтервал от минус восемнадцати до минус двух, включая минус восемнадцать.
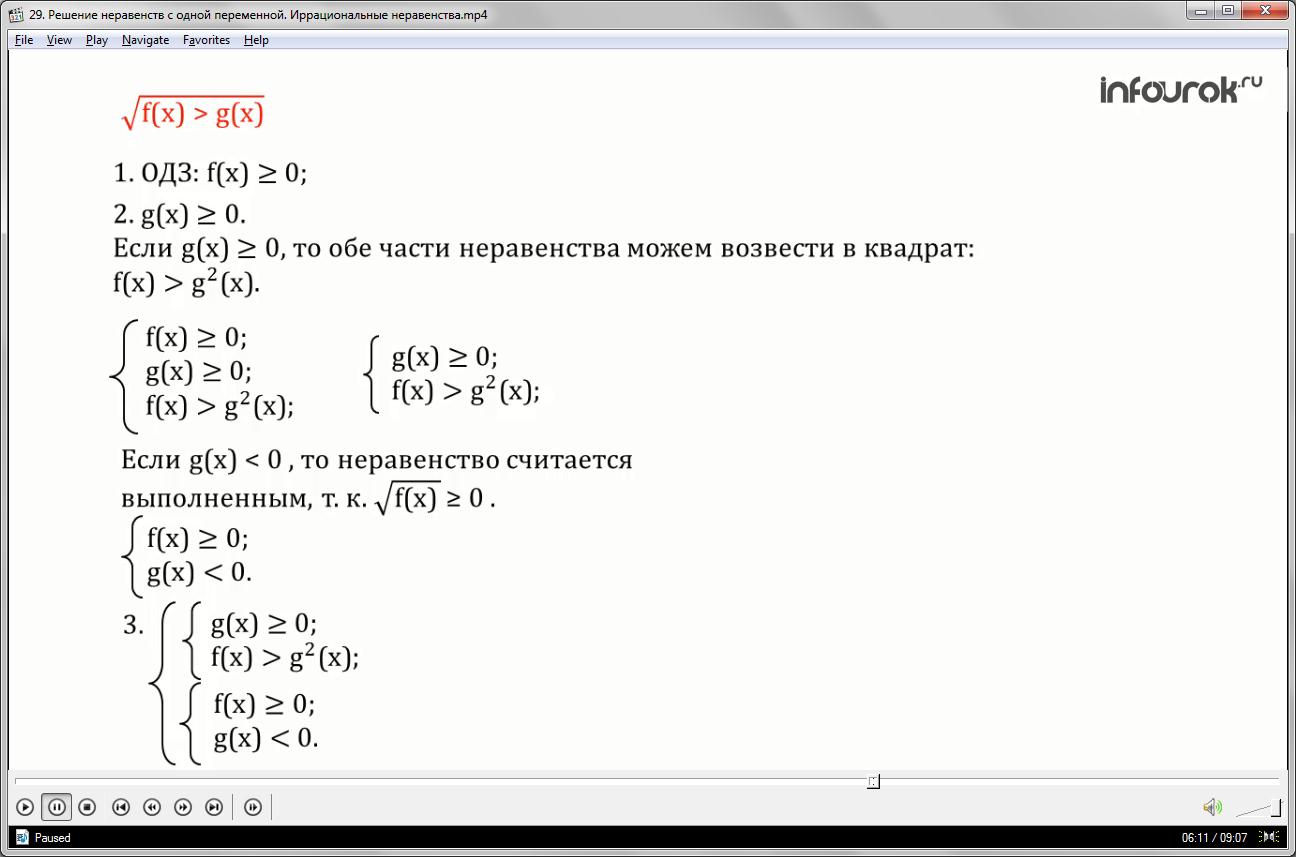
Теперь обсудим решение неравенства квадратный корень из эф от икс больше жэ от икс.
Во-первых, ОДЗ неравенства задается условием эф от икс больше либо равно нулю.
Во-вторых, правая часть неравенства может быть и отрицательной, и неотрицательной.
Поэтому рассмотрим два случая:
если жэ от икс больше либо равно нулю,
то обе части неравенства можем возвести в квадрат и эф от икс больше жэ в квадрате от икс.
Имеем систему неравенств
эф от икс больше либо равно нулю,
жэ от икс больше либо равно нулю,
эф от икс больше жэ в квадрате от икс.
Можно заметить, что если будет выполнено третье неравенство, то будет выполнено и первое, поэтому его можно опустить. Тогда получим систему неравенств
жэ от икс больше либо равно нулю,
эф от икс больше жэ в квадрате от икс.
Если жэ от икс меньше нуля, то неравенство считается выполненным, так как квадратный корень из эф от икс больше либо равно нулю.
Имеем систему неравенств
эф от икс больше либо равно нулю.
жэ от икс меньше нуля.
В-третьих, таким образом, данное иррациональное неравенство равносильно совокупности двух систем неравенств
Первая система:
жэ от икс больше либо равно нулю,
эф от икс больше жэ в квадрате от икс.
Вторая система:
эф от икс больше либо равно нулю.
жэ от икс меньше нуля.
Задание 3
Решить неравенство квадратный корень из трех минус икс больше икс минус один.
Решение
Данное неравенство равносильно совокупности систем неравенств:
Первая система:
три минус икс больше либо равно нулю,
икс минус один меньше нуля;
Вторая система:
икс минус один больше либо равно нулю,
три минус икс больше квадрата разности икс и единицы.
Решим первую систему неравенств
икс меньше либо равно трем,
икс меньше единицы.
Решением является открытый числовой луч от минус бесконечности до единицы.
Решим вторую систему неравенств.
Решением является полуинтервал от единицы до двух, включая один.
Решением совокупности системы неравенств является объединение двух открытых лучей — это открытый луч от минус бесконечности до двух.
Решение данного иррационального неравенства — открытый луч
от минус бесконечности до двух.
Ответ: открытый луч
от минус бесконечности до двух.
Задание 4
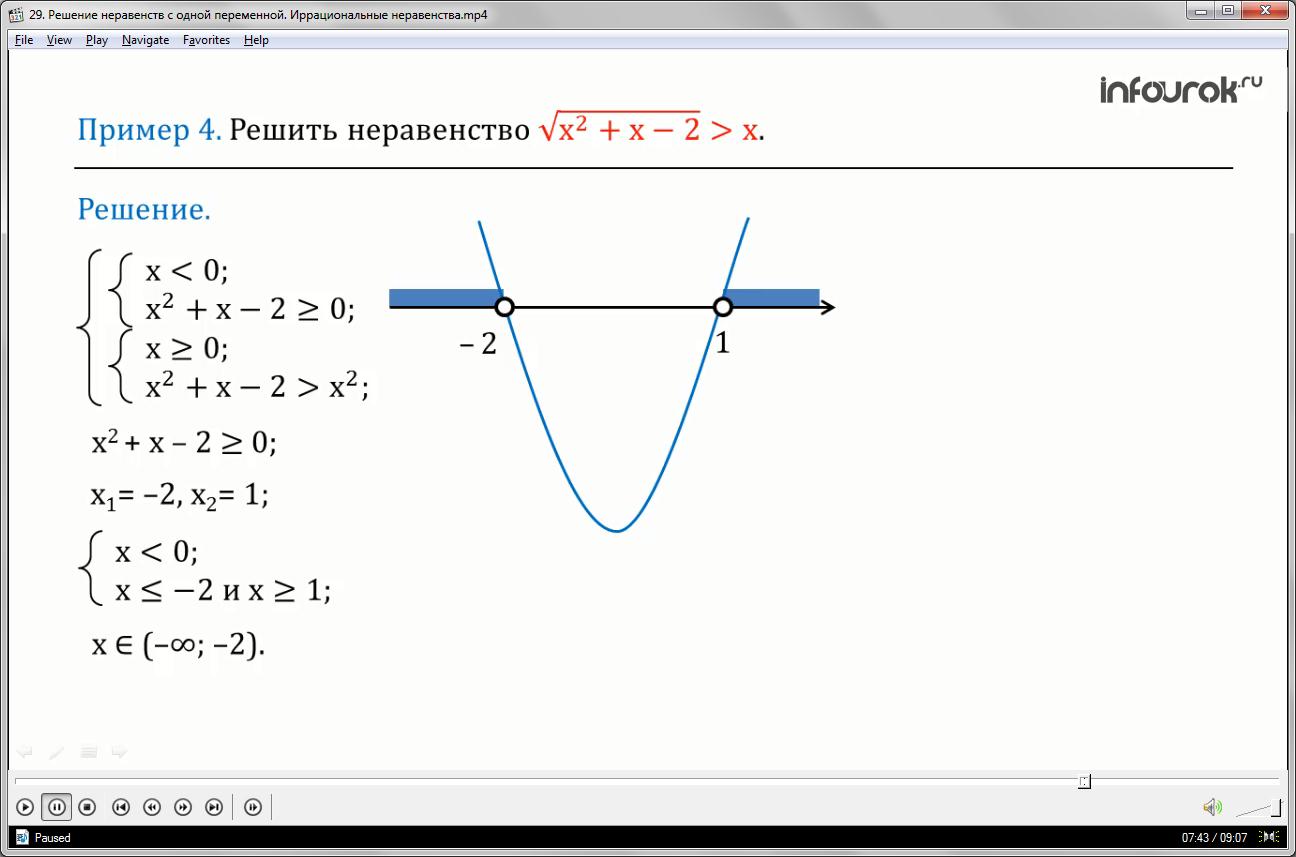
Решить неравенство квадратный корень из икс в квадрате плюс икс минус два больше икс.
Решение
Данное неравенство равносильно совокупности систем неравенств.
Первая система: икс меньше нуля,
икс квадрат плюс икс минус два больше либо равно нулю, обозначим ее номером один.
Вторая система:
икс больше либо равно нулю,
икс квадрат плюс икс минус два больше икс квадрат.
Обозначим ее номером два.
Решим первую систему неравенств.
Для решения квадратного неравенства
икс квадрат плюс икс минус два больше либо равно нулю,
вычислим корни квадратного трехчлена икс квадрат плюс икс минус два,
получим икс первое равно минус двум, икс второе равно единице.
Геометрическая модель помогает найти решение этого неравенства: икс меньше либо равно минус двум и икс больше либо равно единице.
Имеем систему неравенств, равносильную первой:
икс меньше нуля,
икс меньше либо равно минус двум и икс больше либо равно единице.
Решением этой системы, а значит, и первой системы совокупности является числовой луч от минус бесконечности до минус двух.
Решим вторую систему неравенств
икс больше либо равно нулю.
икс квадрат плюс икс минус два больше икс квадрат.
После равносильных преобразований получим систему неравенств:
икс больше либо равно нулю.
икс больше двух.
Решением этой системы, а значит, и второй системы совокупности является открытый луч от двух до плюс бесконечности.
Решением совокупности системы неравенств, а, значит, и исходного иррационального неравенства является объединение числового луча от минус бесконечности до минус двух и открытого числового луча от двух до плюс бесконечности.
Ответ: объединение числового луча от минус бесконечности до минус двух и открытого числового луча от двух до плюс бесконечности.
Сегодня на уроке мы изучили алгоритм решения иррациональных уравнений вида
квадратный корень из эф от икс меньше жэ от икс и квадратный корень из эф от икс больше жэ от икс и научились его применять к решению примеров. На следующем уроке мы изучим разные способы решения неравенств с модулем.
| Автор | |
|---|---|
| Дата добавления | 16.11.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 4963 |
| Номер материала | 1078 |