
Презентация "Минимизация булевых функций" по дисциплине "Элементы математической логики"









Описание презентации по отдельным слайдам:
Минимизация булевых функций Беляева Татьяна Юрьевна ГБПОУ КК «Армавирский машиностроительный техникум» Преподаватель математических дисциплин
Упрощение булевых функций Непосредственно с помощью логических тождеств Алгоритмическими методами карты Карно (при числе переменных не более шести) метод Квайна–Мак–Класки (если переменных больше шести)
Упрощение булевых функций Для минимизации булевых функций используется закон попарного склеивания и поглощения: «Если переменная изменяет свое значение, а функция при этом остается неизменной, то эту переменную можно исключить из выражения» Операция попарного склеивания осуществляется между 2-мя членами (термами), у которых совпадают вхождения для всех переменных, кроме одной. Т.о., главной задачей при минимизации СДНФ и СКНФ является поиск термов, пригодных к склейке с последующим поглощением. Например: 1) f = (x1 /\ x2) \/ (x1 /\ x2) = x1 /\ (x2 \/ x2) = x1 /\ 1 = x1 2) f = (x1 /\ x2 /\ x3 /\ x4) \/ (x1 /\ x2 /\ x3 /\ x4) = (x1 /\ x2 /\ x4) /\ (x3 \/ x3) = x1 /\ x2 /\ x4
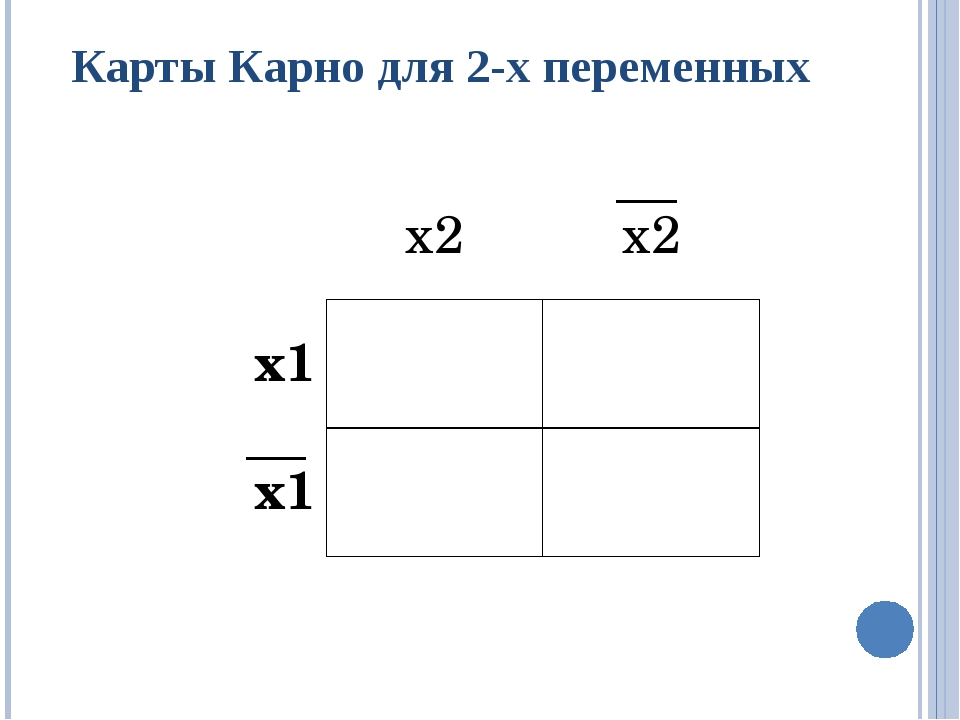
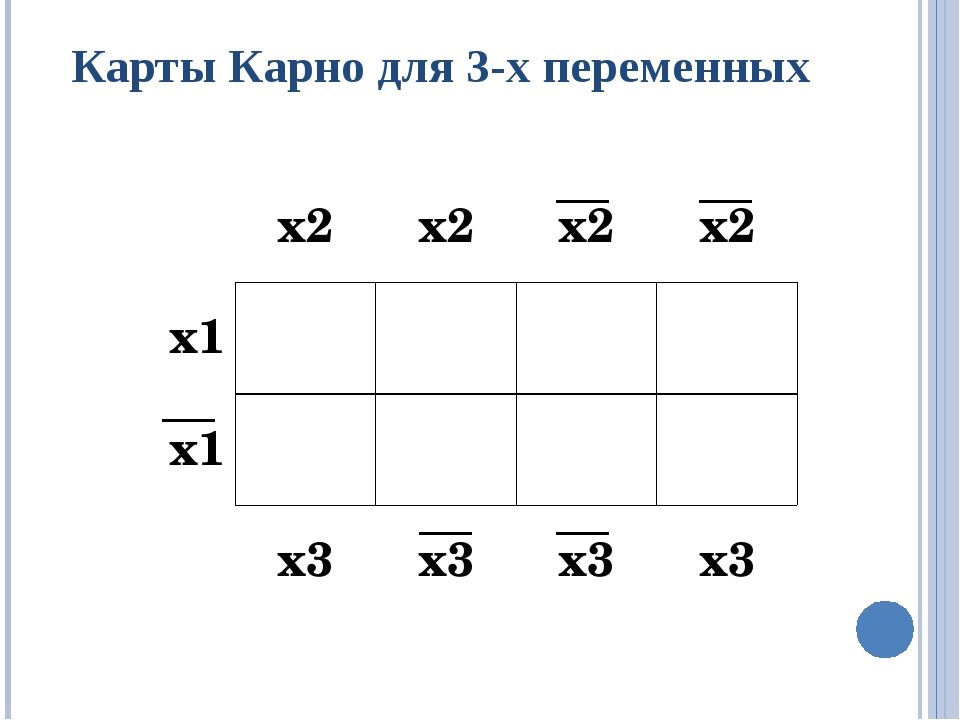
Требования к картам Карно • Число клеток карты равно 2ⁿ, где п - число переменных функции. • Столбцы и строки карты обозначаются прямыми и инверсными переменными данной функции таким образом, чтобы любые соседние клетки по строкам или столбцам отличались бы между собой значением только одной переменной. • Каждая клетка карты соответствует произведению переменных, на пересечении которых она находится. (!!) Клетки, находящиеся на границах одной строки или столбца, также считаются соседними.
Алгоритм работы с картами Карно Для получения минимальной функции охватывают областями все соседние клетки, имеющие значение 1, и исключают переменные, имеющие прямое и инверсное включения. Объединяют клетки по следующим правилам: 1) Число объединяемых клеток может быть равно 2, 4, 8, 16,… 2) Объединять надо как можно больше клеток 3) Самих объединений должно быть как можно меньше
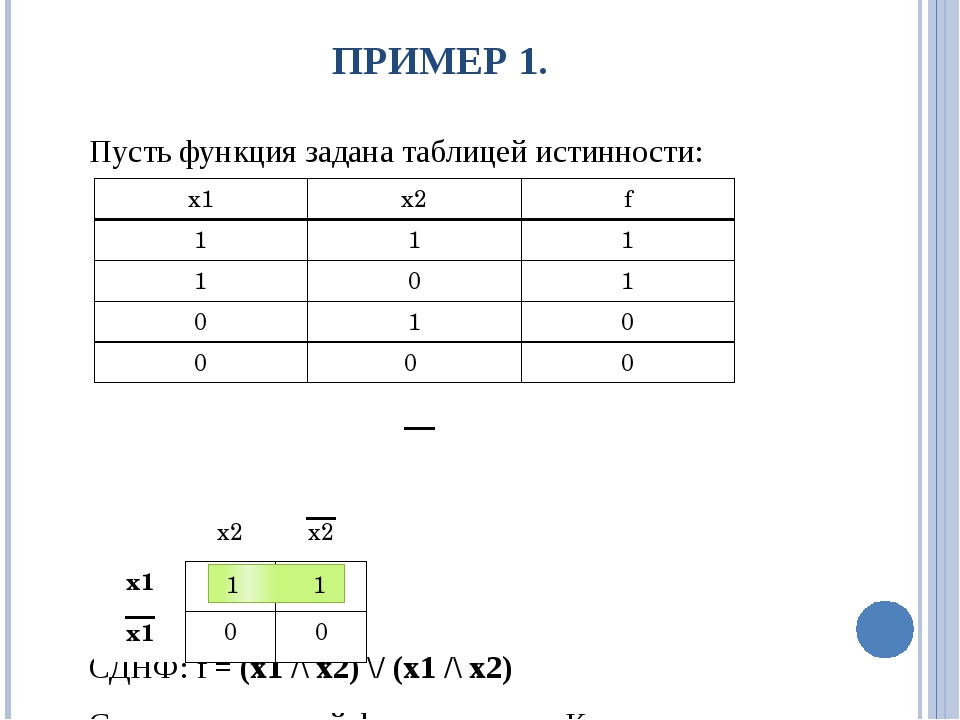
ПРИМЕР 1. Пусть функция задана таблицей истинности: СДНФ: f = (x1 /\ x2) \/ (x1 /\ x2) Составим для этой функции карту Карно: f = x1 1 1 х1 х2 f 1 1 1 1 0 1 0 1 0 0 0 0 х2 х2 х1 1 1 х1 0 0
ПРИМЕР 2. Пусть задана функция: f = (x1 /\ x2 /\ x3) \/ (x1 /\ x2 /\ x3) \/ (x1 /\ x2 /\ x3) \/ (x1 /\ x2 /\ x3) \/ (x1 /\ x2 /\ x3) Составим для этой функции карту Карно: Прямоугольник, содержащий 4 единицы в 1-й строке, позволяет исключить переменные х2 и х3. Прямоугольник, содержащий 2 единицы в 1-м столбце, - переменную х1. Т.о.: f = x1 \/ (x2 /\ x3) 1 1 1 1 1 1 х2 х2 х2 х2 х1 1 1 1 1 х1 1 х3 х3 х3 х3
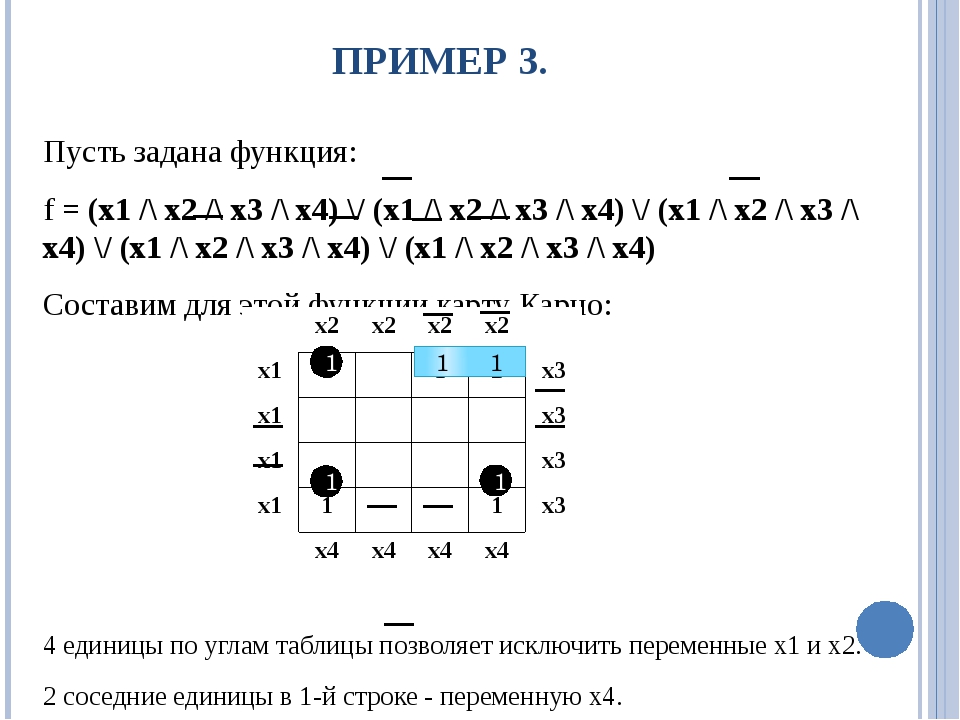
ПРИМЕР 3. Пусть задана функция: f = (x1 /\ x2 /\ x3 /\ x4) \/ (x1 /\ x2 /\ x3 /\ x4) \/ (x1 /\ x2 /\ x3 /\ x4) \/ (x1 /\ x2 /\ x3 /\ x4) \/ (x1 /\ x2 /\ x3 /\ x4) Составим для этой функции карту Карно: 4 единицы по углам таблицы позволяет исключить переменные х1 и х2. 2 соседние единицы в 1-й строке - переменную х4. Т.о.: f = (x3 /\ x4) \/ (x1 /\ x2 /\ x3) 1 1 1 1 1 1 x2 x2 x2 x2 x1 1 1 1 x3 x1 x3 x1 x3 x1 1 1 x3 x4 x4 x4 x4

| Автор | |
|---|---|
| Дата добавления | 21.12.2018 |
| Раздел | Высшая математика |
| Подраздел | Презентация |
| Просмотров | 2113 |
| Номер материала | 6000 |