21.12.2018
1804
0
Бесплатно
Уроки математики / Презентация / Презентация "Операции над множествами" по дисциплине "Дискретная математика"
Презентация "Операции над множествами" по дисциплине "Дискретная математика"
1
из 24
Описание презентации по отдельным слайдам:
№ слайда 1
Операции над множествами Преподаватель ГБПОУ КК «АМТ» Беляева Т.Ю.
№ слайда 2
1. Объединение множеств (сложение) А В
№ слайда 3
1. Объединение множеств (сложение)
№ слайда 4
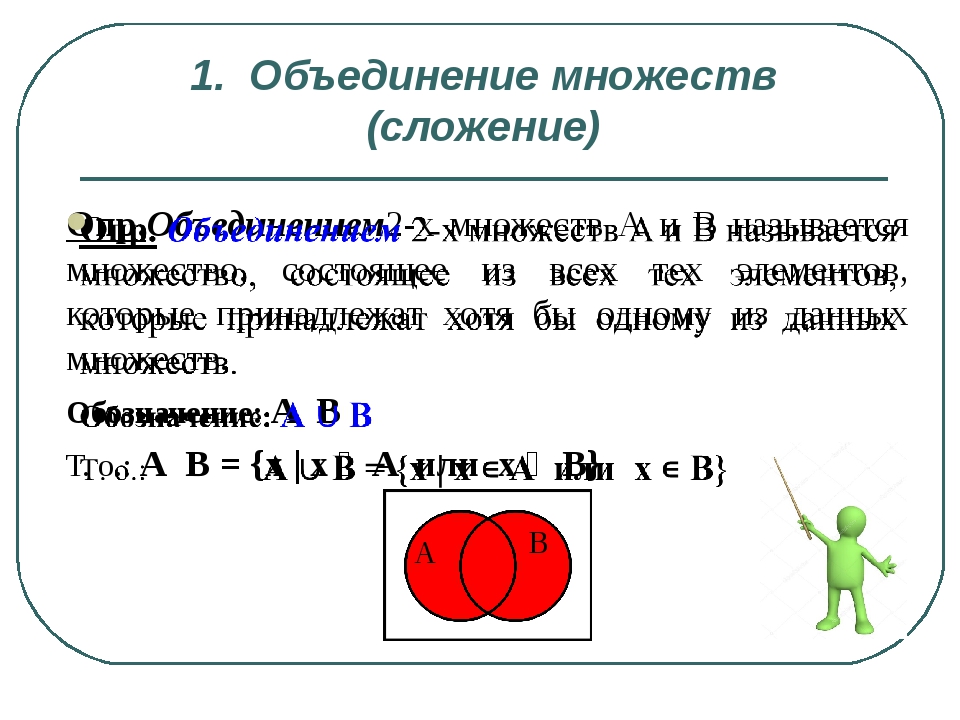
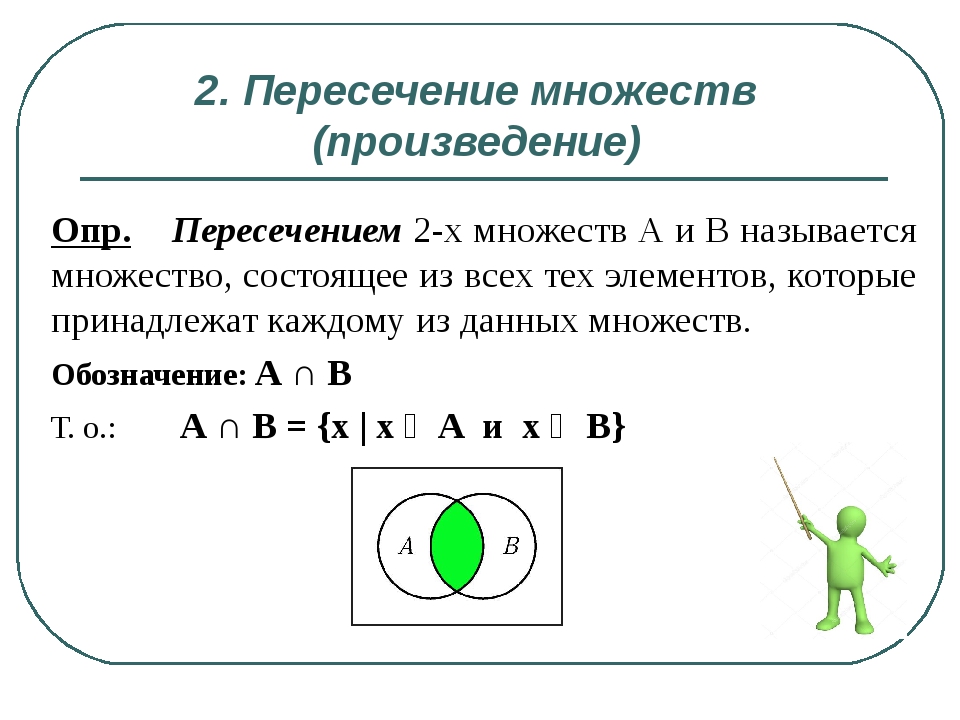
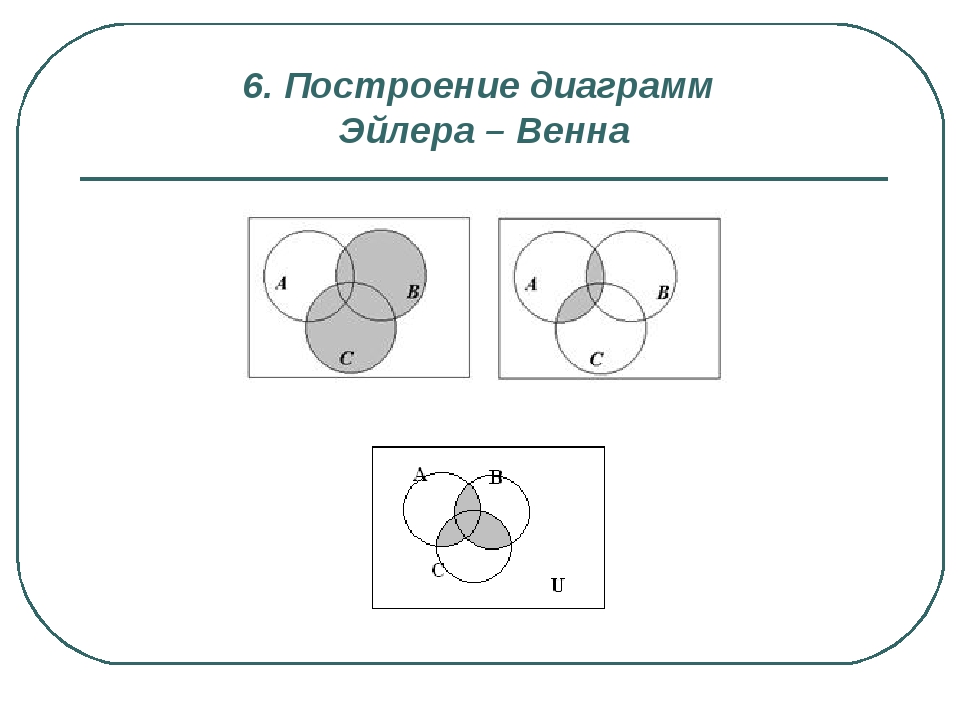
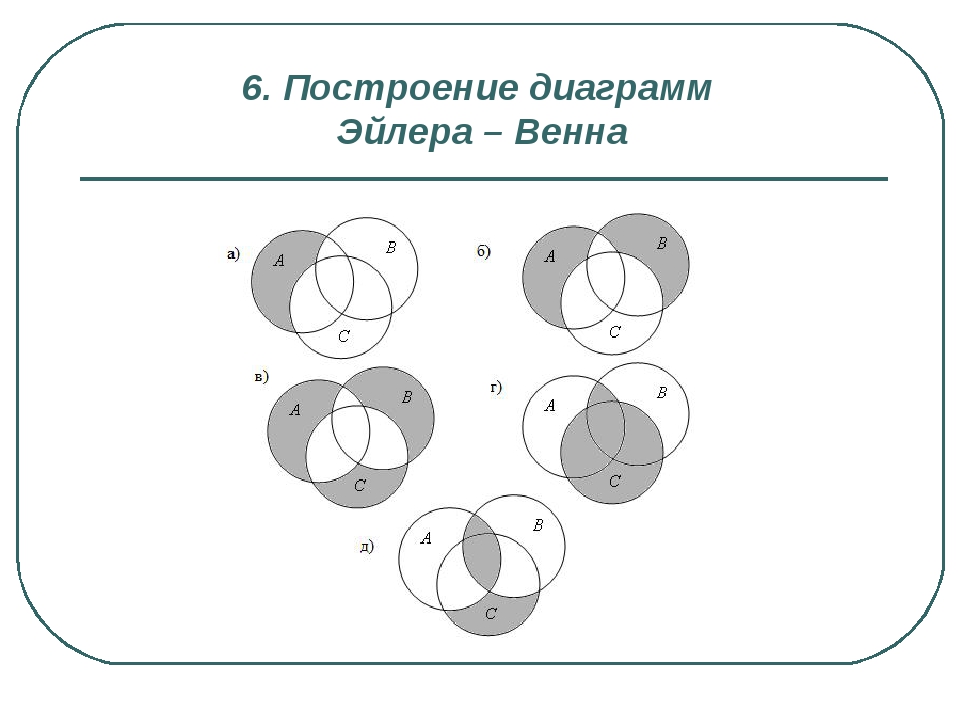
2. Пересечение множеств (произведение) Опр. Пересечением 2-х множеств А и В называется множество, состоящее из всех тех элементов, которые принадлежат каждому из данных множеств. Обозначение: А ∩ В Т. о.: А ∩ В = {x | x ∊ A и x ∊ B}
№ слайда 5
2. Пересечение множеств (произведение) Напр.: 1) {1; 2; 3} ∩ {2; 3; 4} = {2; 3} 2) А = { x | x = 2n, n ∊ Z}, B = {x | x = 3n, n ∊ Z} A ∩ B = { x | x = 6n, n ∊ Z} (!!) 1) Если А – произвольное множество, то А ∩ А = А А ∩ Ø = Ø А ∩ U = А 2) Если А и В – произвольные множества, то А ∩ В = В ∩ А 3) Если А ⊂ В, то В ∩ А = А
№ слайда 6
Обобщение .
№ слайда 7
3. Разность множеств .
№ слайда 8
3. Разность множеств Напр.: {1; 2; 3} \ {2; 3; 4} = { 1 } (!!) Если А – произвольное множество, то А \ А = Ø А \ Ø = А А \ U = Ø В отличии от объединения и пересечения, разность – строго двуместна. .
№ слайда 9
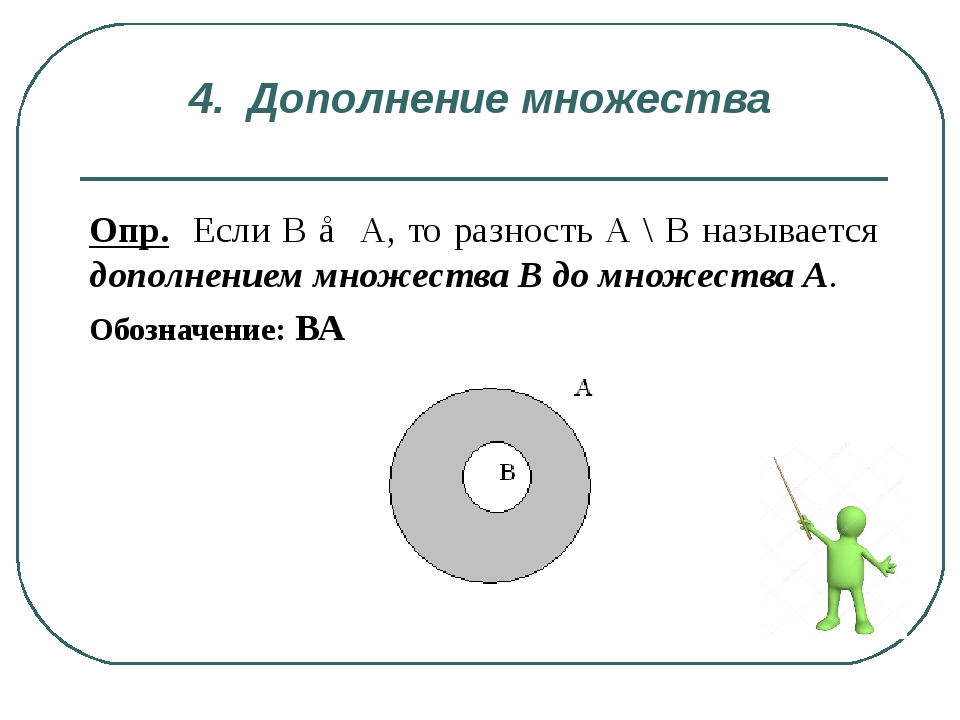
4. Дополнение множества . Опр. Если В ⊂ А, то разность А \ В называется дополнением множества В до множества А. Обозначение: ВА
№ слайда 10
4. Дополнение множества Опр. Дополнением множества А до универсального множества U, или просто дополнением, называется множество всех элементов множества U, не принадлежащих А. Обозначение: Ā По определению: Ā = U \ А
№ слайда 11
4. Дополнение множества
№ слайда 12
5. Дизъюнктивная сумма множеств (симметрическая разность) . Опр. Дизъюнктивной суммой 2-х множеств А и В называется множество, состоящее из всех тех элементов, которые принадлежат или множеству А, или множеству В, но не обоим вместе. Обозначение: А ⊕ В
№ слайда 13
5. Дизъюнктивная сумма множеств (симметрическая разность) . Напр: 1) {1; 2; 3 } ⊕ { 2; 3; 4 } = { 1; 4 } (!!) Если А – произвольное множество, то А⊕ А = Ø А⊕ Ø = А А⊕ U = Ā
№ слайда 14
6. Построение диаграмм Эйлера – Венна
№ слайда 15
6. Построение диаграмм Эйлера – Венна .
№ слайда 16
7. Тождества алгебры множеств, связывающие несколько операций .
№ слайда 17
7. Тождества алгебры множеств, связывающие несколько операций .
№ слайда 18
7. Тождества алгебры множеств, связывающие несколько операций .
№ слайда 19
8. Декартово произведение множеств
№ слайда 20
8. Декартово произведение множеств ПР. А = {1; 2; 3}, B = {2; 4} А × В = {(1; 2), (1; 4), (2; 2), (2; 4), (3; 2), (3; 4)} B × A = {(2; 1), (2; 2), (2; 4), (4; 1), (4; 2), (4; 3)} (!!) 1) А × В ≠ B × A 2) | А × В | = | А | × | В |
№ слайда 21
8. Декартово произведение множеств Опр. Если А = В, то А × В = А × А – декартовый квадрат. Обозначение: А2 Напр.: R2 = R × R - множество точек плоскости (х; у) ПР. А2 = {(1; 1), (1; 2), (1; 3), (2; 1), (2; 2), (2; 3), (3; 1), (3; 2), (3; 3)}
№ слайда 22
8. Декартово произведение множеств Опр. Прямым произведением множеств А1, А2, …, Ап называется множество, состоящее из упорядоченных п- ок. Обозначение: А1 × А2 × … × Ап Опр. Упорядоченную п-ку называют п-мерным вектором или кортежем, а элементы, составляющие п-ку, - ее координатами. (!!) Если все Аi = А, то А × А × … × А = Аn и | Аn | = | A |n
№ слайда 23
8. Декартово произведение множеств
№ слайда 24
8. Декартово произведение множеств ПР. Дано: B = {2; 4} Найти: В3 ПР. Дано: М – множество букв алфавита в русском язык Найти: М4
Бесплатно
| Автор | |
|---|---|
| Дата добавления | 21.12.2018 |
| Раздел | Высшая математика |
| Подраздел | Презентация |
| Просмотров | 6443 |
| Номер материала | 6002 |