
Разработка урока на тему "Правильные многогранники"
Тема: Правильные многогранники.
Тип урока: изучение нового материала и первичное закрепление новых знаний.
Вид урока: комбинированный.
Цели:
Образовательная цель:
способствовать формированию знаний о правильных многогранниках;
помощь в ходе исследовательской работы сделать вывод о соотношениях между числами вершин, граней и ребер выпуклого многогранника.
Развивающая цель:
создать условия для развития познавательного интереса и творческой активности учащихся;
способствовать развитию навыков рационального использования ЭВМ в своей деятельности.
Воспитательная цель:
воспитание чувства ответственности, культуры диалога;
воспитание интереса к математике как учебному предмету через современные технологии преподавания;
создание условий для целостного восприятия общей картины мира.
Формы организации познавательной деятельности: фронтальная, индивидуальная, групповая, коллективная.
Методы и приемы обучения:
объяснительно-иллюстративный; частично-поисковый; исследовательский; словесный; наглядный (демонстрация компьютерных презентаций); практический.
Оборудование:
наборы моделей геометрических тел; каркасные модели правильных многогранников;
экран; мультимедийный проектор; компьютер.
Компьютерное программное обеспечение: программа Microsoft Office PowerPoint 2003.
Структура урока.
Организационный момент.(2 мин.)
Вступительное слово учителя. Ознакомление с темой, постановка цели.
Актуализация опорных знаний.(5 мин.)
Задание практического характера (работа с набором моделей геометрических тел).
Изучение нового материала.(10 мин.)
а). Формированию понятия о правильных многогранниках.
б). Определение видов правильных многогранников.
Исследовательская работа.(15 мин.)
а). Мотивация деятельности. Привлекательная цель.
б). Исследовательская работа.
Первичное осмысление и применение изученного материала.(10 мин.)
а) Решение задач.
б) Отчет по итогам выполнения индивидуального задания по теме «Применение кристаллов»
Постановка домашнего задания.(2 мин.)
Домашнее задание.
Самооценка деятельности. Итог урока.(2 мин.)
Опрос. Рефлексия деятельности.
Ход урока.
Организационный момент.
Вступительное слово учителя:
«Чешский писатель Карел Чапек, восхищаясь формами кристаллов в коллекциях Британского музея, в своих «Записках из Англии» писал: «Я должен еще сказать о кристаллах, формах, красках. Есть кристаллы огромные, как колоннада храма; нежные, как плесень; острые, как шипы; чистые, лазурные, зеленые; как ничто другое в мире, огненные, черные; математически точные, совершенные; похожие на конструкции сумасбродных ученых… И в человеке таится сила кристаллизации. Чтобы быть равным природе, надо быть точным математически и геометрически».
Кристаллами восхищаются поэты, художники, свойства кристаллов изучают различные науки, например, химия, физика, кристаллография. А что в кристаллах, в первую очередь, может привлечь внимание математиков? (Правильная геометрическая форма, кристаллы принимают форму многогранников).
Понятие о многогранниках вам уже знакомо. Цель урока: выделить особую группу многогранников и дать понятие о правильных многогранниках; выявить свойство, характерное для всех выпуклых многогранников, точнее, установить закономерность между числами ребер, граней и вершин выпуклого многогранника. Тема урока: «Правильные многогранники»
Актуализация опорных знаний.
Практическое задание.
Цель: проверка умений работать с понятиями о многогранниках, выпуклых многогранниках; развитие пространственного мышления.
Работа с моделями следующих тел: тетраэдра, куба, октаэдра, икосаэдра, додекаэдра, цилиндра, конуса, пирамиды, призмы, параллелепипеда, невыпуклого многогранника.
Задание1: Перед вами на столе модели геометрических тел.
Отложите в сторону те модели, которые не являются моделями многогранников.
В другую сторону модели невыпуклых многогранников.
Оставьте перед собой только модели правильных многогранников.
Что называется многогранником?
Какие многогранники называют выпуклыми?
Изучение нового материала.
а). Формированию понятия о правильных многогранниках.
Учащиеся формулируют определение правильного многогранника (с помощью сравнения моделей).
Закрепление понятия о правильных многогранниках
б). Определение видов правильных многогранников.
Учитель перед учениками ставит проблему: «Много ли существует видов правильных многогранников?».
Ученики дают различные предположения о том, как установить количество видов правильных многогранников? (Все грани – правильные многоугольники; все многогранные углы должны быть равны, в каждую вершину должно сходиться одинаковое число ребер, граней, значит нужно установить, сколько граней может сходиться в одну вершину; должен существовать многогранный угол правильного многогранника, условие существования – сумма всех его плоских углов меньше 4d (360°) и т.д.).
Оформляется работа в тетрадях, задание 2.
Задание2.
I. Грань – правильный треугольник.
a3 – внутренний угол треугольника.
a3 = 60°
n – число граней многогранного угла.
1).n = 3 60° · 3 = 180° < 360° Вывод: Существует 3 вида
2).n = 4 60° · 4 = 240° < 360° правильных многогранников,
3).n = 5 60° · 5 = 300° < 360° гранями которых являются
4).n = 6 60° · 6 = 360° (многогранный правильные треугольники.
угол совпадает с плоскостью)
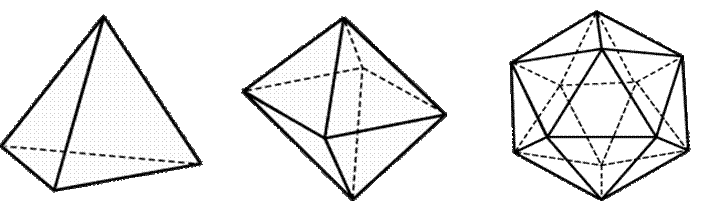
Рис.1
Тетраэдр Октаэдр Икосаэдр
___________________________________________________________________________
I I. Грань – квадрат.
a4 = внутренний угол квадрата.
a4 = 90°
1).n = 3 90° · 3 = 270° < 360° Вывод: Существует 1 вид
2).n = 4 90° · 4 = 360° (многогранный правильного многогранника,
угол совпадает с плоскостью) гранями которого являются
квадраты.
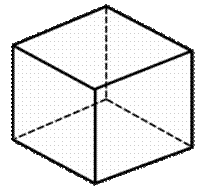 Рис. 2. Куб (гексаэдр)
Рис. 2. Куб (гексаэдр)
___________________________________________________________________________
I I I. Грань – правильный пятиугольник.
a5 = 180° · (5 – 2) / 5 = 108°
1).n = 3 108° · 3 = 324° < 360° Вывод: Существует 1 вид
2).n = 4 108° · 4 = 432° > 360° правильного многогранника,
гранями которого являются
правильные пятиугольники.
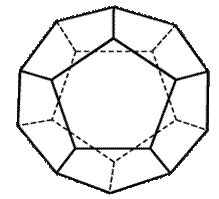 Рис. 3. Додекаэдр
Рис. 3. Додекаэдр
___________________________________________________________________________
I V. Грань – правильный шестиугольник.
a6 = 120° Вывод: правильный многогранник
1).n = 3 120° · 3 = 360° (многогранный гранями которого являются
гол совпадает с плоскостью) правильные шестиугольники
не существует.
Вывод: существует 5 видов правильных многогранников.
Почему правильные многогранники получили такие имена?
Это связано с числом их граней. В переводе с греческого языка:
эдрон – грань окто - восемь
тетра - четыре додека - двенадцать
гекса - шесть икоси - двадцать
Исследовательская работа.
Исследовательская работа: задание №3.
Проблема: Найти зависимость между числами ребер, граней и вершин выпуклого многогранника.
Цель: Выявить зависимость между числами ребер, граней и вершин выпуклого многогранника.
Гипотеза: Если существует зависимость между числами ребер, граней и вершин, то ее можно выразить формулой и по ней найти число ребер выпуклого многогранника?
Заполняется таблица с помощью учителя.
| Название правиль-ного многогранника | Вид грани | Число вер-шин ( В ) | Числогра- ней ( Г ) | Число ребер ( Р ) | Вывод из наблюдений |
| Четырехгранник (тетраэдр) | правильный треугольник | 4 | 4 | 6 | В+Г=Р+2 |
| Шестигранник (куб-гексаэдр) | квадрат | 8 | 6 | 12 | В+Г=Р+2 |
| Восьмигранник (октаэдр) | правильный треугольник | 6 | 8 | 12 | В+Г=Р+2 |
| Двенадцатигранник (додекаэдр) | правильный пятиугольник | 20 | 12 | 30 | В+Г=Р+2 |
| Двадцатигранник (икосаэдр) | правильный треугольник | 12 | 20 | 30 | В+Г=Р+2 |
Вывод: В+Г=Р+2.
Учитель сообщает: «Теорема носит название Декарта – Эйлера. Эйлер нашел и проверил эту зависимость. За сто лет до Эйлера эта теорема была сформулирована Декартом, но не доказана. Теорема верна не только для правильных многогранников, но и для любых выпуклых многогранников и даже для некоторых невыпуклых».
Первичное осмысление и применение изученного материала.
а) Решение задач. Существуют другие свойства, устанавливающие зависимость между элементами выпуклого многогранника.
Задача1: «Доказать, что сумма величин всех плоских углов на поверхности выпуклого многогранника, образуемых его ребрами, равна 360°´( Р - Г)».
Задача2 (шуточного содержания): «Муха движется вдоль ребер выпуклого многогранника. Может ли муха обойти все вершины этого многогранника, проходя по каждому ребру только один раз?»
Постановка домашнего задания.
Стр.312, вопросы 36,37.
Стр.318, № 79.
Модели многогранников.
Самооценка деятельности. Итог урока.
Кристалл является символом неживой природы, но согласно современным данным, молекула ДНК представляет собой одномерный апериодический кристалл. Следовательно, кристаллы – это не только символ неживой природы, но и основа жизни на Земле.
Литература.
Винниджер. Модели многогранников. - М.: Просвещение, 1975.
Гетман А.П.. Сокровища России. – М.: Просвещение,1987.
Геометрия: Учеб. для 10-11 кл. общеобразоват. учреждений/ Атанасян Л.С., Бутузов В.Ф., Кардомцев С.Б. и др.–5-е изд.– М.: Просвещение, 2002.
Гросман С., Тернер Дж. Математика для биологов. - М.: Просвещение, 1983.
Кабардин С.И.,.Шедер Н.И. Факультативный курс физики. – М.: Просвещение, 1989.
Кованцов Н.И. Математика и романтика. - Киев, 1976.
Смирнова И.М. В мире многогранников. - М.: Просвещение, 1990.
Философия: Учебник для высших учебных заведений. – Ростов н/Д.: Феникс, 1998, 576 с.
Чанышев А.Н. Курс лекция по древней и средневековой философии: Учеб. Пособие для вузов. – М.: Высш. шк., 1991, 512 с.
Шафрановский И.И. Симметрия в природе. - Л., 1988.
Web ресурсы.

| Автор | |
|---|---|
| Дата добавления | 20.10.2019 |
| Раздел | Геометрия |
| Подраздел | Конспект урока |
| Просмотров | 1842 |
| Номер материала | 6364 |