
Сборник игр по математике для дошкольников
Сборник игр
направленных
на развитие
элементарных
математических
представлений
детей дошкольного возраста
Пояснительная записка
Огромную роль в умственном воспитании и в развитии интеллекта играет математика. В математике заложены огромные возможности для развития мышления детей, в процессе их обучения с самого раннего возраста.
Дошкольный возраст- это период, когда главный вид деятельности малыша- это игра. В игре легче усваиваются знания, умения и навыки, поэтому все занятия с ребенком должны быть организованы в игровой форме.
Формированию у ребенка математических представлений способствует использование разнообразных дидактических игр. Такие игры учат ребенка понимать некоторые сложные математические понятия, формируют представление о соотношении цифры и числа, количества и цифры, развивают умения ориентироваться в направлениях пространства, делать выводы. При использовании дидактических игр широко применяются различные предметы и наглядный материал, который способствует тому, что занятия проходят в веселой, занимательной и доступной форме. Применение дидактических игр повышает эффективность педагогического процесса, кроме того, они способствуют развитию памяти, мышления у детей, оказывая огромное влияние на умственное развитие ребенка.
В детском саду ставятся такие педагогические задачи: развивать у детей память, внимание, мышление, воображение, так как без этих качеств немыслимо развитие ребенка в целом. Используя различные дидактические игры, занимательные упражнения можно также исправить пробелы знаний у детей. Все дидактические игры можно разделить на несколько групп: игры с цифрами и числами; игры путешествие во времени; игры на ориентировки в пространстве; игры с геометрическими фигурами; игры на логическое мышление.
Логические приемы умственных действий - сравнение, обобщение, анализ, синтез, классификация, сериация, аналогия, систематизация, абстрагирование - в литературе также называют логическими приемами мышления. При организации специальной развивающей работы над формированием и развитием логических приемов мышления наблюдается значительное повышение результативности этого процесса независимо от исходного уровня развития ребенка.
Развивать логическое мышление дошкольника целесообразнее всего в русле математического развития. Еще более повышает процесс усвоения ребенком знаний в этой области использование заданий, активно развивающих мелкую моторику, то есть заданий логико-конструктивного характера. Кроме того, существуют различные приемы умственных действий, которые помогают усилить эффективность использования логико-конструктивных заданий.
Сериация - построение упорядоченных возрастающих или убывающих рядов по выбранному признаку. Классический пример сериации: матрешки, пирамидки, вкладные мисочки и т. д.
Анализ - выделение свойств объекта, или выделение объекта из группы, или выделение группы объектов по определенному признаку.
Синтез - соединение различных элементов (признаков, свойств) в единое целое. В психологии анализ и синтез рассматриваются как взаимодополняющие друг друга процессы (анализ осуществляется через синтез, а синтез - через анализ).
Психологически способность к синтезу формируется у ребенка раньше, чем способность к анализу. То есть, если ребенок знает, как это было собрано (сложено, сконструировано), ему легче анализировать и выделять составные части. Именно поэтому столь серьезное значение уделяется в дошкольном возрасте деятельности, активно формирующей синтез, - конструированию.
Сравнение - логический прием умственных действий, требующий выявления сходства и различия между признаками объекта (предмета, явления, группы предметов).
Показателем сформированности приема сравнения будет умение ребенка самостоятельно применять его в деятельности без специальных указаний взрослого на признаки, по которым нужно сравнивать объекты.
Классификация - разделение множества на группы по какому-либо признаку, который называют основанием классификации. Классификацию можно проводить либо по заданному основанию, либо с заданием поиска самого основания (этот вариант чаще используется с детьми шести-семи лет, так как требует определенного уровня сформированности операций анализа, сравнения и обобщения).
Классификацию с детьми дошкольного возраста можно проводить:
- по названию (чашки и тарелки, ракушки и камешки, кегли и мячики и т. д.);
- по размеру (в одну группу большие мячи, в другую - маленькие, в одну коробку длинные карандаши, в другую - короткие и т. д.);
- по цвету (в эту коробку красные пуговицы, в эту - зеленые);
- по форме (в эту коробку квадраты, а в эту - кружки; в эту коробку - кубики, в эту - кирпичики и т. д.);
- по другим признакам нематематического характера: что можно и что нельзя есть; кто летает, кто бегает, кто плавает; кто живет в доме и кто в лесу; что бывает летом и что зимой; что растет в огороде и что в лесу и т. д.
Обобщение - это оформление в словесной (вербальной) форме результатов процесса сравнения.
Обобщение формируется в дошкольном возрасте как выделение и фиксация общего признака двух или более объектов. Обобщение хорошо понимается ребенком, если является результатом деятельности, произведенной им самостоятельно, например классификации: эти все - большие, эти все - маленькие; эти все - красные, эти все - синие; эти все - летают, эти все - бегают и др.
Все приведенные выше примеры сравнений и классификаций завершались обобщениями. Для дошкольников возможны эмпирические виды обобщения, то есть обобщения результатов своей деятельности. Для подведения детей к такого рода обобщениям взрослый соответствующим образом организует работу над заданием: подбирает объекты деятельности, задает вопросы в специально разработанной последовательности, чтобы подвести ребенка к нужному обобщению. При формулировке обобщения следует помогать ребенку правильно его построить, употребить нужные термины и словесные обороты.
Логическое развитие ребенка предполагает также формирование умения понимать и прослеживать причинно-следственные связи явлений и умения выстраивать простейшие умозаключения на основе причинно-следственной связи. Легко убедиться, что при выполнении всех приведенных выше примеров заданий и систем заданий ребенок упражняется в этих умениях, поскольку в их основе также лежат умственные действия: анализ, синтез, обобщение и др.
Цель математического развития дошкольников
Всестороннее развитие личности ребенка.
Подготовка к успешному обучению в школе.
Коррекционно-воспитательная работа.
Задачи математического развития дошкольников
1. Формирование системы элементарных математических представлений.
Формирование предпосылок математического мышления.
Формирование сенсорных процессов и способностей.
Расширение и обогащение словаря и совершенствование связанной речи.
Формирование начальных форм учебной деятельности.
Упорядоченные представления, правильно сформированные первые понятия, вовремя развитые мыслительные способности, служат залогом дальнейшего успешного обучения детей в школе.
Психологические исследования убеждают, что в процессе обучения происходят качественные изменения в психическом развитии ребенка.
С ранних лет важно не только сообщать детям готовые зна ния, но и развивать умственные способности детей, научить их самостоятельно, осознанно получать знания и использовать их в жизни.
Обучение в повседневной жизни носит эпизодический ха рактер. Для математического развития важно, чтобы все знания давались систематически и последовательно. Знания в области математики должны усложняться постепенно с учетом возраста и уровня развития детей.
Важно организовать накопление опыта ребенка, научить его пользоваться эталонами (формы, величины и др.), рациональны ми способами действия (счета, измерения, вычислений и др.).
Учитывая незначительный опыт детей, обучение идет пре имущественно индуктивным путем: сначала накапливаются с по мощью взрослого конкретные знания, затем они обобщаются в правила и закономерности. Необходимо использовать и дедук тивный метод: сначала усвоение правила, затем его применение, конкретизация и анализ.
Для осуществления грамотного обучения дошкольников, их математического развития воспитатель сам должен знать пред мет науки математики, психологические особенности развития математических представлений детей и методику работы.
Возможности всестороннего развития ребенка в процессе ФЭМП
I. Сенсорное развитие (ощущение и восприятие) Источником элементарных математических представлений является окружающая реальная действительность, которую ребе нок познает в процессе разнообразной деятельности, в общении со взрослыми и под их обучающим руководством.
II. Развитие мышления
наглядно-действенное;
наглядно-образное;
словесно-логическое.
III. Развитие памяти, внимания, воображения
IV. Развитие речи
обогащение словаря (числительные, пространственные предлоги и наречия, математические термины, характери зующие форму, величину и др.);
согласование слов в единственном и множественном числе («один зайчик, два зайчика, пять зайчиков»);
формулировка ответов полным предложением;
логические рассуждения.
V. Развитие специальных навыков и умений
VI. Развитие познавательных интересов
активизирует восприятие и мыслительную деятельность;
расширяет кругозор;
способствует умственному развитию;
повышает качество и глубину знаний;
способствует успешному применению знаний на практике;
побуждает самостоятельно приобретать новые знания;
меняет характер деятельности и связанные с ней пережива ния (деятельность становится активной, самостоятельной, разносторонней, творческой, радостной, результативной);
оказывает положительное влияние на формирование лич ности;
оказывает положительное действие на здоровье ребенка (возбуждает энергию, повышает жизненный тонус, делает жизнь более счастливой);
Пути возбуждения интереса к математике:
связь новых знаний с детским опытом;
открытие новых сторон в прежнем опыте детей;
игровая деятельность;
словесное возбуждение;
стимуляция.
Психологические предпосылки интереса к математике:
• создание положительного эмоционального отношения к педагогу;
• создание положительного отношения к занятиям.
Пути возбуждения познавательного интереса к занятию по ФЭМП:
объяснение смысла выполняемой работы («Кукле негде спать. Давайте построим для нее кровать! Каких размеров она должна быть? Давайте померяем!»);
работа с любимыми привлекательными объектами (игруш ками, сказками, картинками и др.);
связь с близкой детям ситуацией («У Миши день рожде ния. Когда у вас день рожденья, кто к вам приходит?
К Мише тоже пришли гости. Сколько чашек надо поста вить на стол для праздника?»);
интересная для детей деятельность (игра, рисование, кон струирование, аппликация и др.);
посильные задания и помощь в преодолении трудностей (ребенок должен в конце каждого занятия испытать удовле творение от преодоления трудностей)', положительное отношение к деятельности детей (заинтере сованность, внимание к каждому ответу ребенка, доброже лательность); побуждение инициативы и др.
Принципы обучения математике
Сознательность и активность.
Наглядность.
Деятельностный подход.
Систематичность и последовательность.
Прочность.
Постоянная повторяемость.
Научность.
Доступность.
Связь с жизнью.
Развивающее обучение.
Индивидуальный и дифференцированный подход.
Коррекционная направленность и др.
Методы ФЭМП. Методы организации и осуществления учебно-познавательной деятельности
1. Перцептивный аспект (методы, обеспечивающие передачу учебной информации педагогом и восприятие ее детьми посред ством слушания, наблюдения, практических действий):
а) словесный (объяснение, беседа, инструкция, вопросы и др.);
б) наглядный (демонстрация, иллюстрация, рассматривание и др.);
в) практический (предметно-практические и умственные дей ствия, дидактические игры и упражнения и др.).
2. Гностический аспект (методы, характеризующие усвоение нового материала детьми, — путем активного запоминания, пу тем самостоятельных размышлений или проблемной ситуации):
а) иллюстративно-объяснительный;
б) проблемный;
в) эвристический;
г) исследовательский и др.
3. Логический аспект (методы, характеризующие мыслитель ные операции при подаче и усвоении учебного материала):
а) индуктивный (от частного к общему);
б) дедуктивный (от общего к частному).
4. Управленческий аспект (методы, характеризующие степень самостоятельности учебно-познавательной деятельности детей):
а) работа под руководством педагога,
б) самостоятельная работа детей.
Особенности практического метода:
выполнение разнообразных предметно-практических и ум ственных действий;
широкое использование дидактического материала;
возникновение математических представлений в результате действия с дидактическим материалом;
выработка специальных математических навыков (счета, измерения, вычислений и др.);
использование математических представлений в быту, игре, труде и др.
Особенности наглядного метода
Виды наглядного материала:
демонстрационный и раздаточный;
сюжетный и бессюжетный;
объемный и плоскостной;
специально-счетный (счетные палочки, абак, счеты и др.);
фабричный и самодельный.
Методические требования к применению наглядного мате риала:
• новую программную задачу лучше начинать с сюжетного объемного материала;
по мере усвоения учебного материала переходить к сюжетно-плоскостной и бессюжетной наглядности;
одна программная задача объясняется на большом разно образии наглядного материала;
новый наглядный материал лучше показать детям заранее...
Требования к самодельному наглядному материалу:
гигиеничность (краски покрываются лаком или пленкой, бархатная бумага используется только для демонстрацион ного материала);
эстетичность;
реальность;
разнообразие;
однородность;
прочность;
логическая связанность (заяц — морковь, белка — шишка и т. п.);
достаточное количество...
Особенности словесного метода
Вся работа построена на диалоге воспитатель — ребенок.
Требования к речи воспитателя:
эмоциональная;
грамотная;
доступная;
четкая;
достаточно громкая;
приветливая;
в младших группах тон загадочный, сказочный, таинствен ный, темп небыстрый, многократные повторения;
в старших группах тон заинтересовывающий, с использова нием проблемных ситуаций, темп достаточно быстрый, приближающийся к ведению урока в школе...
Требования к речи детей:
грамотная;
понятная (если у ребенка плохое произношение, воспита тель проговаривает ответ и просит повторить); полными предложениями;
с нужными математическими терминами;
достаточно громкая...
Приемы ФЭМП
Демонстрация (обычно используется при сообщении но вых знаний).
Инструкция (используется при подготовке к самостоятель ной работе).
Пояснение, указание, разъяснение (используются для пре дотвращения, выявления и устранения ошибок).
Вопросы к детям.
Словесные отчеты детей.
Предметно-практические и умственные действия.
Контроль и оценка.
Требования к вопросам воспитателя:
точность, конкретность, лаконизм;
логическая последовательность;
разнообразие формулировок;
небольшое, но достаточное количество;
избегать подсказывающих вопросов;
умело пользоваться дополнительными вопросами;
давать детям время на обдумывание...
Требования к ответам детей:
краткие или полные в зависимости от характера вопроса;
на поставленный вопрос;
самостоятельные и осознанные;
точные, ясные;
достаточно громкие;
грамматически правильные...
Что делать, если ребенок отвечает неправильно?
(В младших группах необходимо исправить, попросить по вторить правильный ответ и похвалить. В старших — можно сде лать замечание, вызвать другого и похвалить правильно ответив шего.)
Критерии оценки математических умений детей 5-6 лет
Основы математических представлений детей 5-6 лет оцениваются по следующим критериям:
- Умение сравнивать предметы по их свойствам
- Умение считывать предметы, игрушки от понятий один -много до счёта от одного ,двух, трёх, пяти ( в зависимости от возраста ребёнка)
- Умение считать до десяти вперёд и назад
- Умение считать десятками вперёд и назад
- Умение относить последнее числительное ко всем пересчитанным предметам (один, два, три -всего три кружка)
- Умение сравнивать что больше, а что меньше.
- Умение называть сколько всего. Умение считывать предметы
- Умение сравнивать что получилось, если убрать или если прибавить машинку, кружок.
- Умение формировать представление о равенстве и неравенстве
- Умение понимать количество предметов, находить цифру и точку по количеству предметов, фигур, игрушек.
- Умение находить правильно на рисунке форму и цвет.
- Умение обводить по рисунку предмет, цифру, букву(письмо)
- Умение представлять геометрические фигуры: шар, куб, цилиндр, пирамида, треугольник, квадрат.
- Умение определять признаки фигур по наличию, отсутствию углов, подвижности, устойчивости.
- Умение различать цвета от "основных" и далее.
- Умение определять направление от себя (вперёд-назад, направо - налево, вверх-вниз)
- Умение ориентироваться во времени: день, ночь, утро, сегодня, завтра, вчера
Упражнения на развитие анализа
1. КАКОЙ КУСОЧЕК ПОДОЙДЕТ?
Материал: рисунок А и рисунок Б.
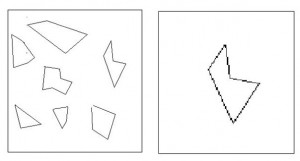
Задание: внимательно рассмотреть рисунки А и Б. Найти на рисунке А такую же фигуру как на рисунке Б.
2. НАЙДИ ОДИНАКОВЫЕ.
Материал: таблица с геометрическими фигурами.
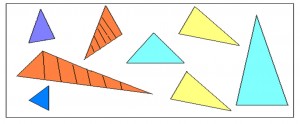
Задание: рассмотреть предложенные геометрические фигуры, назвать их. Найти два одинаковых треугольника.
3. Упражнение
Материал: набор фигур - пять кругов (синие: большой и два маленьких, зеленые: большой и маленький), маленький красный квадрат.

Задание: «Определи, какая из фигур в этом наборе лишняя. (Квадрат.) Объясни почему. (Все остальные - круги.)».
4.Упражнение
Материал: набор фигур - пять кругов (синие: большой и два маленьких, зеленые: большой и маленький).

Задание: «Оставшиеся круги раздели на две группы. Объясни, почему так разделил. (По цвету, по размеру.)».
5. Упражнение
Материал: тот же и карточки с цифрами 2 и 3.
Задание: «Что на кругах означает число 2? (Два больших круга, два зеленых круга.) Число 3? (Три синих круга, три маленьких круга.)».
6. Упражнение
Материал: тот же и дидактический набор (набор пластиковых фигурок: цветные квадраты, круги и треугольники).

Задание: «Вспомни, какого цвета был квадрат, который мы убрали? (Красного.) Открой коробочку, Дидактический набор. Найди красный квадрат. Какого цвета еще есть квадраты? Возьми столько квадратов, сколько кругов (см. упражнения 2, 3). Сколько квадратов? (Пять.) Можно сложить из них один большой квадрат? (Нет.) Добавь столько квадратов, сколько нужно. Сколько ты добавил квадратов? (Четыре.) Сколько их теперь? (Девять.)».
Традиционной формой заданий на развитие визуального анализа являются задания на выбор "лишней" фигуры (предмета). Приведем несколько заданий для детей пяти-шести лет.
Упражнения на развитие синтеза
1. ЧТО ЗА ЧЕМ?
Материал: карточки с рисунками.
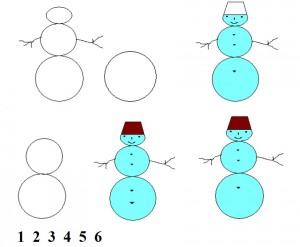
Задания: рассмотреть внимательно рисунки, пронумеровать порядок выполнения рисунка.
2. СОБЕРИ КАРТИНКУ
Материал: карточка с несложным рисунком, разделенная на несколько частей.
Задания: рассмотреть части рисунка, соединить их так, чтобы получилась целая картинка.
Упражнения на сравнение
1. Упражнение
Материал: изображения двух яблок маленькое желтое и большое красное. У ребенка набор фигур: треугольник синий, квадрат красный, круг маленький зеленый, круг большой желтый, треугольник красный, квадрат желтый.

Задание: «Найди среди своих фигур похожую на яблоко». Взрослый по очереди предлагает рассмотреть каждое изображение яблока. Ребенок подбирает похожую фигуру, выбирая основание для сравнения: цвет, форма. «Какую фигурку можно назвать похожей на оба яблока? (Круги. Они похожи на яблоки формой.)».
2. Упражнение
Материал: тот же и набор карточек с цифрами от 1 до 9.

Задание: «Отложи направо все желтые фигуры. Какое число подходит к этой группе? Почему 2? (Две фигуры.) Какую другую группу можно подобрать к этому числу? (Треугольник синий и красный - их два; две красные фигуры, два круга; два квадрата - разбираются все варианты.)». Ребенок составляет группы, с помощью рамки-трафарета зарисовывает и закрашивает их, затем подписывает под каждой группой цифру 2. «Возьми все синие фигуры. Сколько их? (Одна.) Сколько здесь всего цветов? (Четыре.) Фигур? (Шесть.)».
3.Упражнение
Материал: рисунок фигурок-рожиц.

Задание: «Одна из фигурок отличается от всех других. Какая? (Четвертая.) Чем она отличается?»
4. Упражнение
Материал: рисунок фигурок-человечков.

Задание: «Среди этих фигурок есть лишняя. Найди ее. (Пятая фигурка.) Почему она лишняя?»
Более сложной формой такого задания является задание на выделение фигуры из композиции, образованной наложением одних форм на другие. Такие задания можно предлагать детям пяти - семи лет.
5. Упражнение
Материал: рисунок двух маленьких треугольников, образующих один большой.
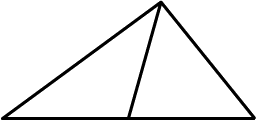
Задание: «На этом рисунке спрятано три треугольника. Найди и покажи их».
Примечание. Нужно помочь ребенку правильно показать треугольники (обвести маленькой указкой или пальцем).
В качестве подготовительных полезно использовать задания, требующие от ребенка синтеза композиций из геометрических фигур на вещественном уровне (из вещественного материала).
6. Упражнение
Материал: 4 одинаковых треугольника.
![]()
Задание: «Возьми два треугольника и сложи из них один. Теперь возьми два других треугольника и сложи из них еще один треугольник, но другой формы. Чем они отличаются? (Один высокий, другой - низкий; один узкий, другой - широкий.) Можно ли сложить из этих двух треугольников прямоугольник? (Да.) Квадрат? (Нет.)».
7. НАЙДИ МЕСТО.
Материал: схема с рисунками, набор геометрических фигур.
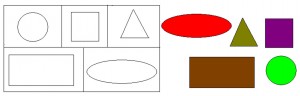
Задание: рассмотреть схему, найти среди предложенных геометрических фигур такие же как на схеме, заполнить схему.
9. НАЙДИ ЗАПЛАТКУ.
Материал: таблицы с рисунками, наклейки геометрических фигур.
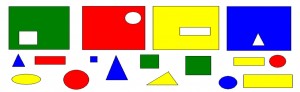
Задание: найти заплатку соответствующего цвета и формы.
Упражнения на обобщение
1. Что лишнее?
Материал: таблица с рисунками.

Задание: рассмотреть фигуры, назвать чем они похожи, какая фигура лишняя и почему.
2. НАЙДИ ЗНАКОМЫЕ ФИГУРЫ
Материал: карточки с рисунками.
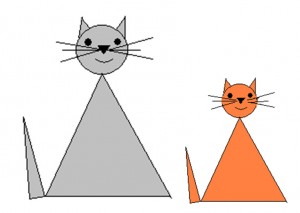
Задание: рассмотреть рисунки, определить, что на них изображено, какие геометрические фигуры для этого потребовались, найти все треугольники на рисунках.
3. Упражнение
Материал: набор из шести фигур разной формы.

Задание: «Одна из этих фигур лишняя. Найди ее. (Фигура 4.)». Детям этого возраста незнакомо понятие выпуклости, но они обычно всегда указывают на эту фигуру. Объяснять они могут так: «У нее угол ушел внутрь». Такое объяснение вполне подходит. «Чем похожи все остальные фигуры? (У них 4 угла, это четырехугольники.)».
При подборе материала для задания взрослый должен следить за тем, чтобы не получился набор, ориентирующий ребенка на несущественные признаки объектов, что будет подталкивать к неверным обобщениям. Следует помнить, что при эмпирических обобщениях ребенок опирается на внешние видимые признаки объектов, что не всегда помогает правильно раскрыть их сущность и определить понятие.
Например, в упражнении 14 фигура 4, в общем, тоже является четырехугольником, но невыпуклым. С фигурами такого рода ребенок познакомится только в девятом классе средней школы, где в учебнике геометрии формулируется определение понятия "выпуклая плоская фигура". В данном случае первая часть задания была ориентирована на операцию сравнения и выделения фигуры, отличающейся по внешней форме от других фигур данной группы. Но обобщение сделано по группе фигур с характерными признаками, часто встречающихся четырехугольников. Если у ребенка возникает интерес к фигуре 4, взрослый может отметить, что это тоже четырехугольник, но необычной формы. Формирование у детей способности самостоятельно делать обобщения является крайне важным с общеразвивающей точки зрения.
Далее приведем пример нескольких взаимосвязанных упражнений (заданий) логико-конструктивного характера по формированию представления о треугольнике для детей пяти лет. Для моделирующей конструктивной деятельности ребенок используют счетные палочки, рамку-трафарет с прорезями в форме геометрических фигур, бумагу, цветные карандаши. Взрослый также использует палочки и фигуры.
4. Упражнение
Цель упражнения - подготовить ребенка к последующей моделирующей деятельности посредством простых конструктивных действий, актуализировать счетные умения, организовать внимание.
Материал: счетные палочки двух цветов.
Задание: «Возьми из коробки столько палочек, сколько у меня (две). Положи перед собой так же (вертикально рядом). Сколько палочек? (Две.) Какого цвета у тебя палочки (палочки в коробке двух цветов: красные и зеленые)? Сделай так, чтобы они были разного цвета. Какого цвета у тебя палочки? (Одна - красная, одна - зеленая.) Один да один.
Сколько вместе? (Две.)».
5. Упражнение
Цель упражнения - организация конструктивной деятельности по образцу.
Упражнения в счете, развитие воображения, речевой деятельности.
Материал: счетные палочки двух цветов.
Задание: «Возьми еще одну палочку и положи ее сверху. Сколько стало палочек?
Сосчитаем. (Три.) На что похожа фигура? (На ворота, на букву «П».) Какие слова начинаются на «П»?»
6. Упражнение
Цель упражнения - развитие наблюдательности, воображения и речевой деятельности. Формирование умения оценивать количественную характеристику видоизменяющейся конструкции (без изменения количества элементов).
Материал: счетные палочки двух цветов.
Примечание: первое задание упражнения является также подготовительным к правильному восприятию смысла арифметических действий.
Задание: «Верхнюю палочку переложи так (взрослый сдвигает палочку вниз, чтобы она оказалась посередине вертикально лежащих палочек). Изменилось ли количество палочек? Почему не изменилось? (Палочку переставили, но не убрали и не добавили.) На что теперь похожа фигура? (На букву «Н».) Назови слова, начинающиеся на «Н».
7. Упражнение
Цель упражнения - формирование конструкторских умений, воображения, памяти и внимания.
Материал: счетные палочки двух цветов.
Задание: «Что еще можно сложить из трех палочек? (Ребенок складывает фигурки и буквы. Называет их, придумывает слова.)».
8. Упражнение
Цель упражнения - формирование образа треугольника, первичное обследование модели треугольника.
Материал: счетные палочки двух цветов, нарисованный взрослым треугольник.
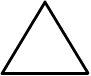
Задание: «Сложи из палочек фигуру». Если ребенок сам не сложил треугольник, взрослый помогает ему. «Сколько палочек понадобилось для этой фигуры? (Три.) Что это за фигура? (Треугольник.) Почему он так называется? (Три угла.)». Если ребенок не может назвать фигуру, взрослый подсказывает ее название и просит ребенка объяснить, как он его понимает. Далее взрослый просит обвести фигуру пальцем, сосчитать углы (вершины), касаясь их пальцем.
9. Упражнение
Цель упражнения - закрепление образа треугольника на кинестетическом (тактильные ощущения) и визуальном уровне. Распознавание треугольников среди других фигур (объем и устойчивость восприятия). Обводка и штриховка треугольников (развитие мелких мышц руки).
Примечание: задание является проблемным, поскольку на используемой рамке есть несколько треугольников и фигур, похожих на них острыми углами (ромб, трапеция).
Материал: рамка-трафарет с фигурами разной формы.
Задание: «Найди на рамке треугольник. Обведи его. Закрась треугольник по рамке».
Штриховка производится внутри рамки, кисть движется свободно, карандаш «стучит» по рамке.
10. Упражнение
Цель упражнения - закрепление визуального образа треугольника. Распознавание нужных треугольников среди других треугольников (точность восприятия). Развитие воображения и внимания. Развитие мелкой моторики.
Задание: «Посмотри на этот рисунок: вот кошка-мама, кот-папа и котенок. Из каких фигур они составлены? (Круги и треугольники.) Какой треугольник нужен для котенка? Для кошки-мамы? Для кота-папы? Нарисуй своего кота». Затем ребенок дорисовывает остальных кошек, ориентируясь на образец, но самостоятельно. Взрослый обращает внимание на то, что кот-папа самый высокий. «Правильно поставь рамку, чтобы кот-папа получился самый высокий».
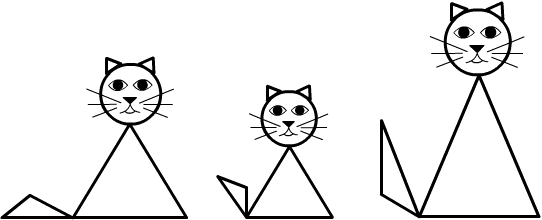
Примечание: данное упражнение не только способствует накоплению у ребенка запасов образов геометрических фигур, но и развивает пространственное мышление, поскольку фигуры на рамке-трафарете расположены в различных положениях, и чтобы найти нужную, необходимо узнать ее в другой позиции, а затем повернуть рамку для ее рисования в такой позиции, которую требует рисунок.
Очевидно, что конструктивная деятельность ребенка в процессе выполнения данных упражнений развивает не только математические способности и логическое мышление ребенка, но и его внимание, воображение, тренирует моторику, глазомер, пространственные представления, точность и т. д.
Каждое из приведенных упражнений направлено на формирование логических мыслительных приемов. Например, упражнение 15 учит ребенка сравнивать; упражнение 16 - сравнивать и обобщать, а также анализировать; упражнение 17 учит анализу и сравнению; упражнение 18 - синтезу; упражнение 19 - анализу, синтезу и обобщению; упражнение 20 - фактическая классификация по признаку; упражнение 21 учит сравнению, синтезу и элементарной сериации.
Упражнения на классификацию
1. ТРИ ОБРУЧА.
Материал: лист бумаги А4 с тремя кругами, наклейки геометрических фигур.
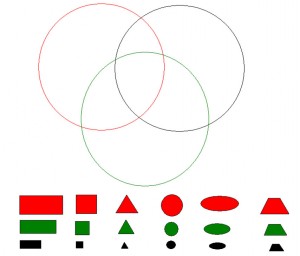
Задание: разместить в каждом круге геометрические фигуры соответствующего цвета. Задание можно усложнить, например, предложить детям разместить фигуры так, чтобы в красном круге не было фигур с углами и т. д.
2. РАЗЛОЖИ ЦИФРЫ
Материал: пять наборов цифр от 1 до 5 разного вида.

Задание: разложить цифры каждого вида в отдельный ряд таблицы.
3. Упражнение
Материал: несколько кругов одинакового размера, но разного цвета (два цвета).
Задание: «Раздели круги на две группы. По какому признаку это можно сделать? (По цвету.)».
4. Упражнение
Материал: к предыдущему набору добавляются несколько квадратов тех же цветов (два цвета). Фигуры перемешиваются.
Задание: «Попробуй снова разделить фигуры на две группы». Возможны два варианта разделения: по форме и по цвету. Взрослый помогает ребенку уточнить формулировки. Ребенок говорит обычно: «Эти - круги, эти – квадраты». Взрослый обобщает: «Значит, разделили по форме».
Упражнения на сериацию
1. РАССТАВЬ ПО-ПОРЯДКУ.
Материал: карточки с рисунками.

2. РАЗЛОЖИ ПО РОСТУ.
Материал: бумажные полоски разного размера и цвета.

Задание: разложить полоски по длине, начиная с самой длинной.
Количество и счёт
Задание № 1
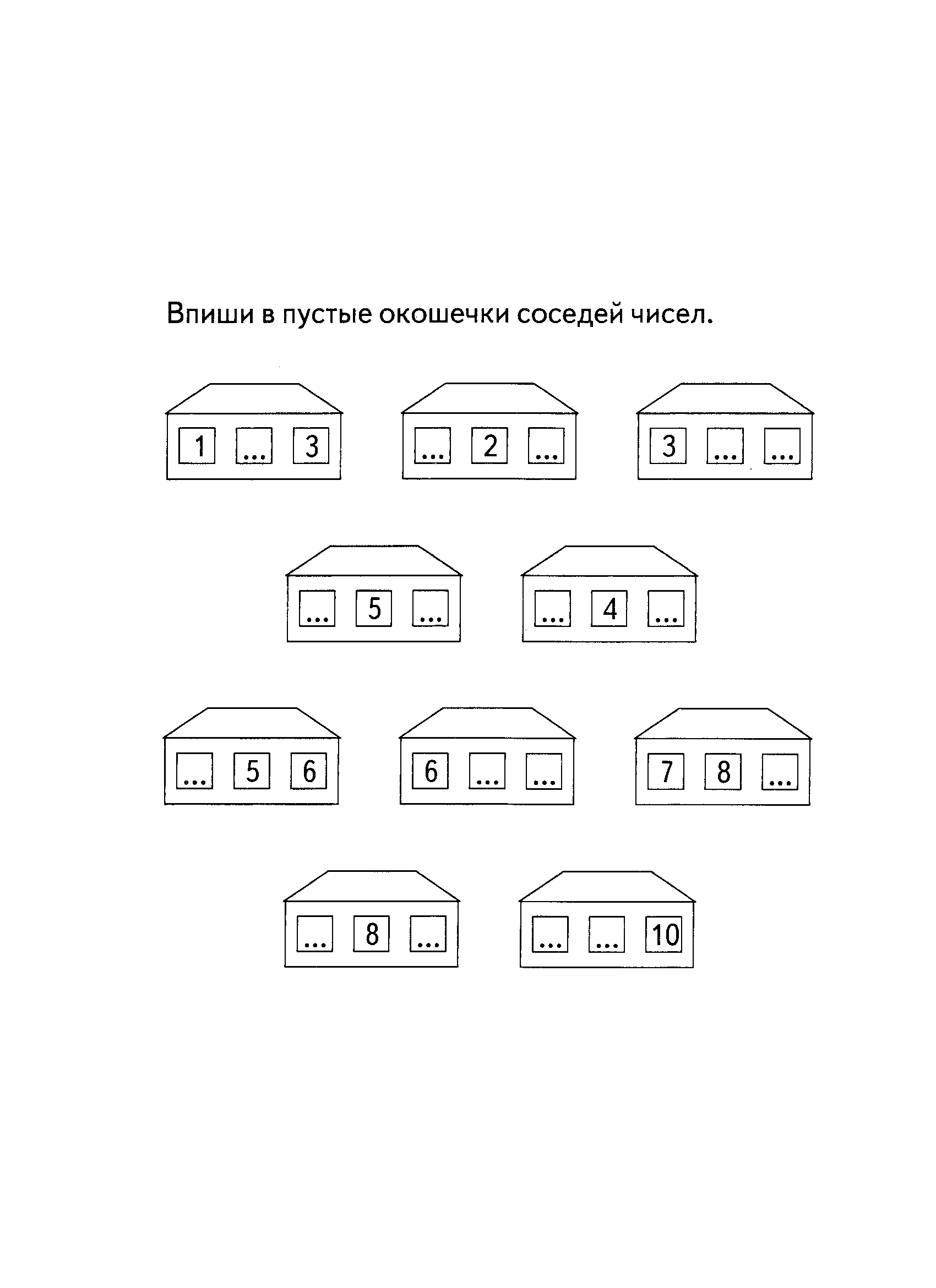
Задание № 2
Количество и счёт
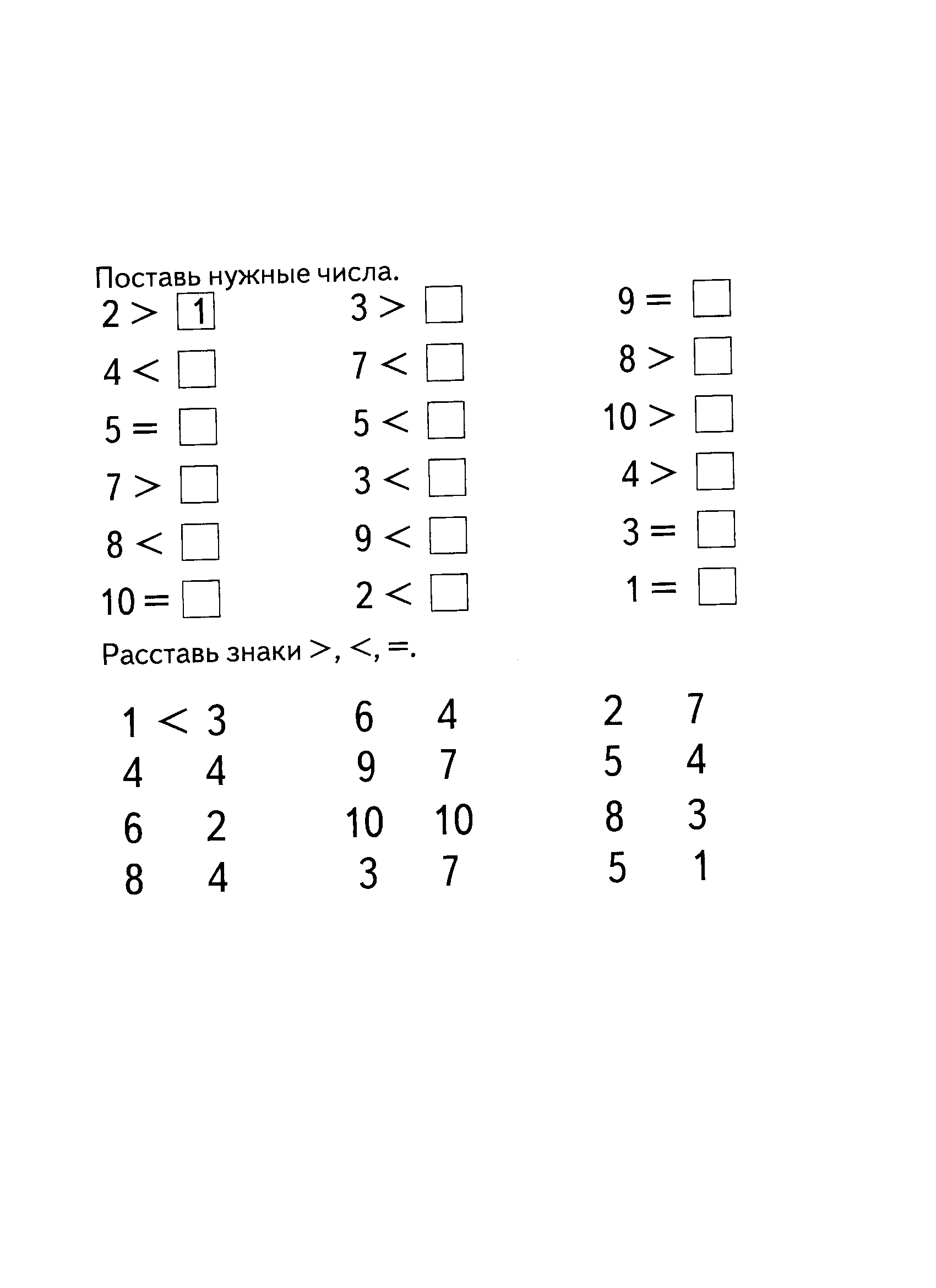
Задание № 3
Количество и счёт
Задание № 4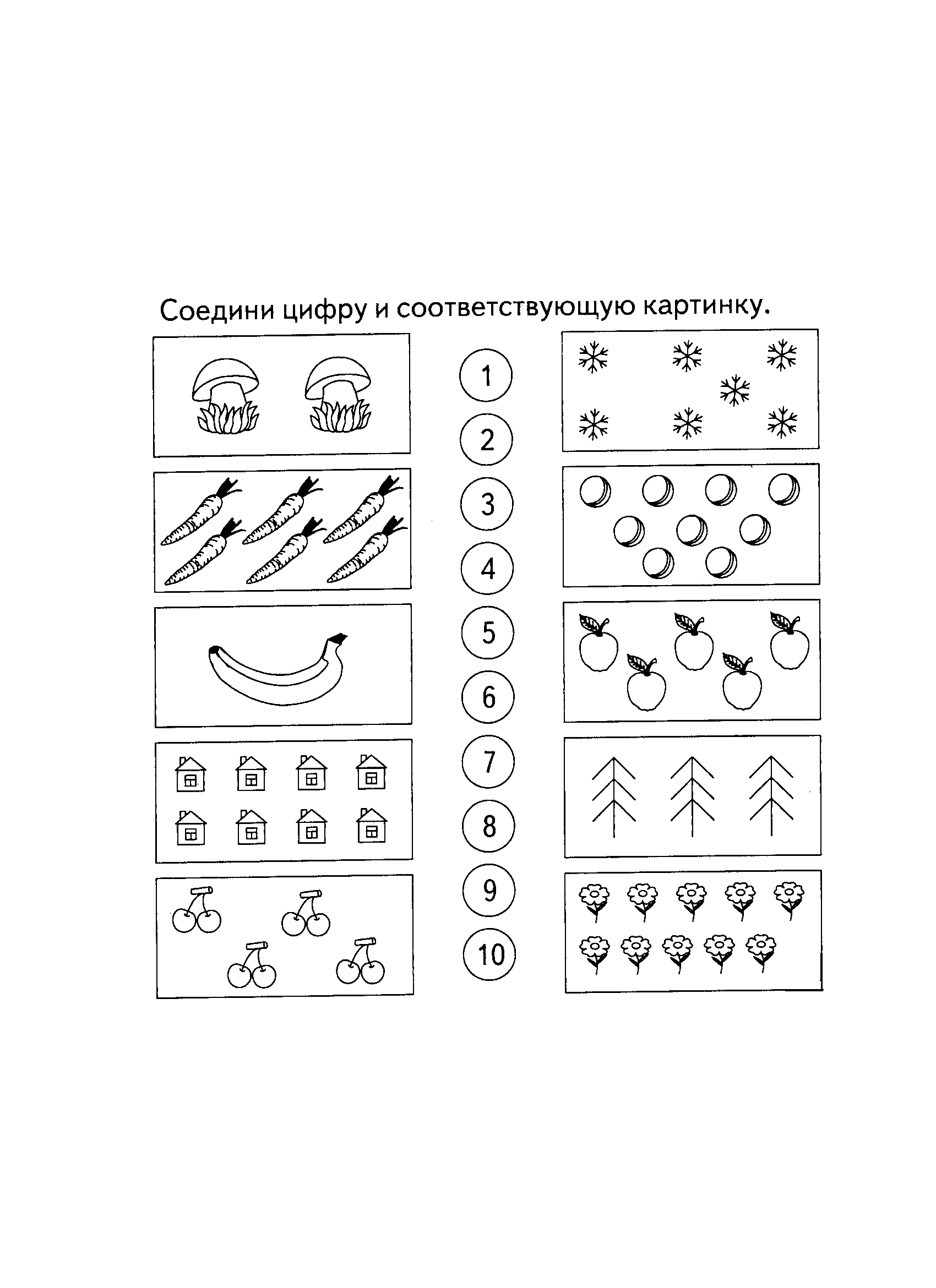
Количество и счёт
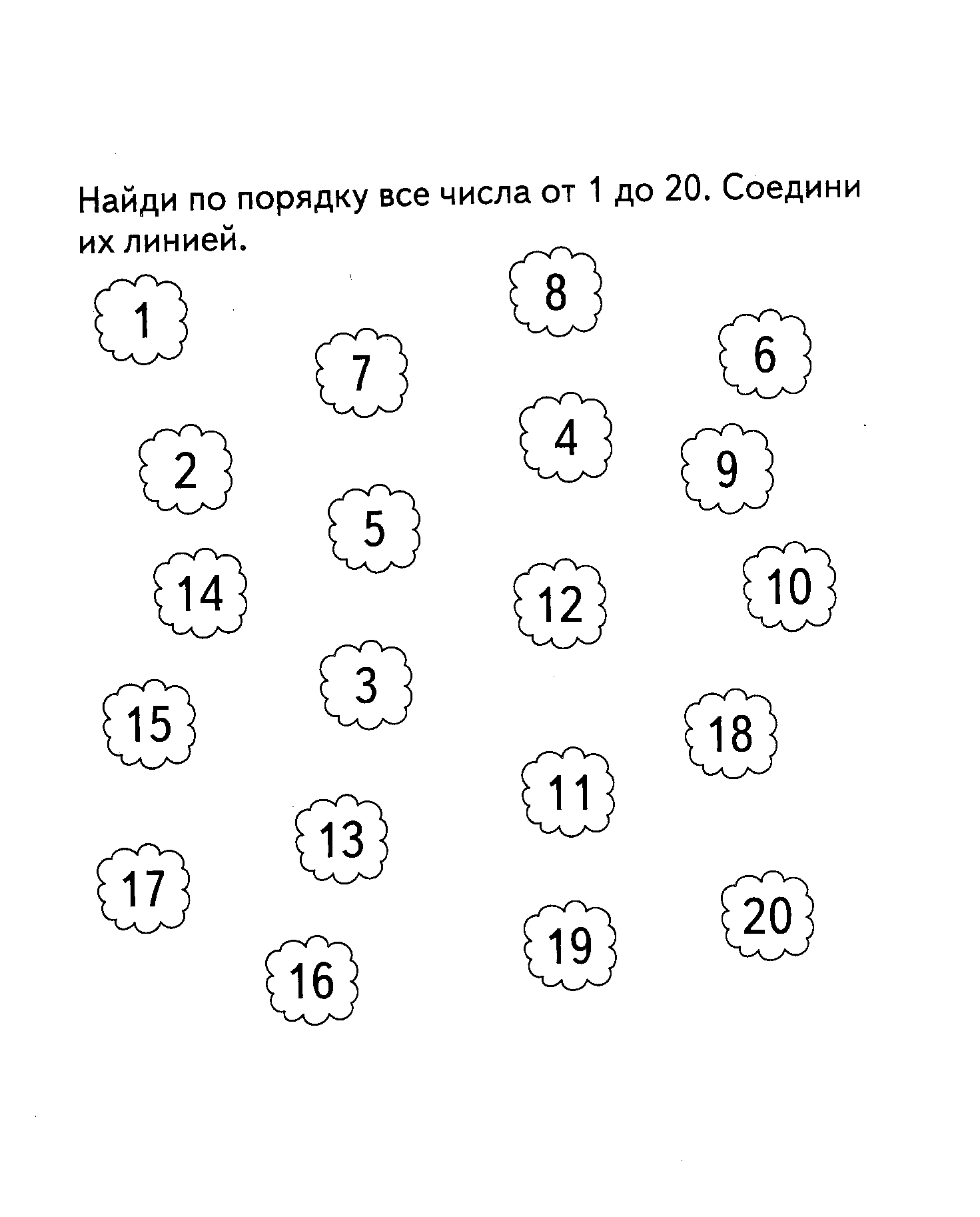
Задание № 5
Количество и счёт
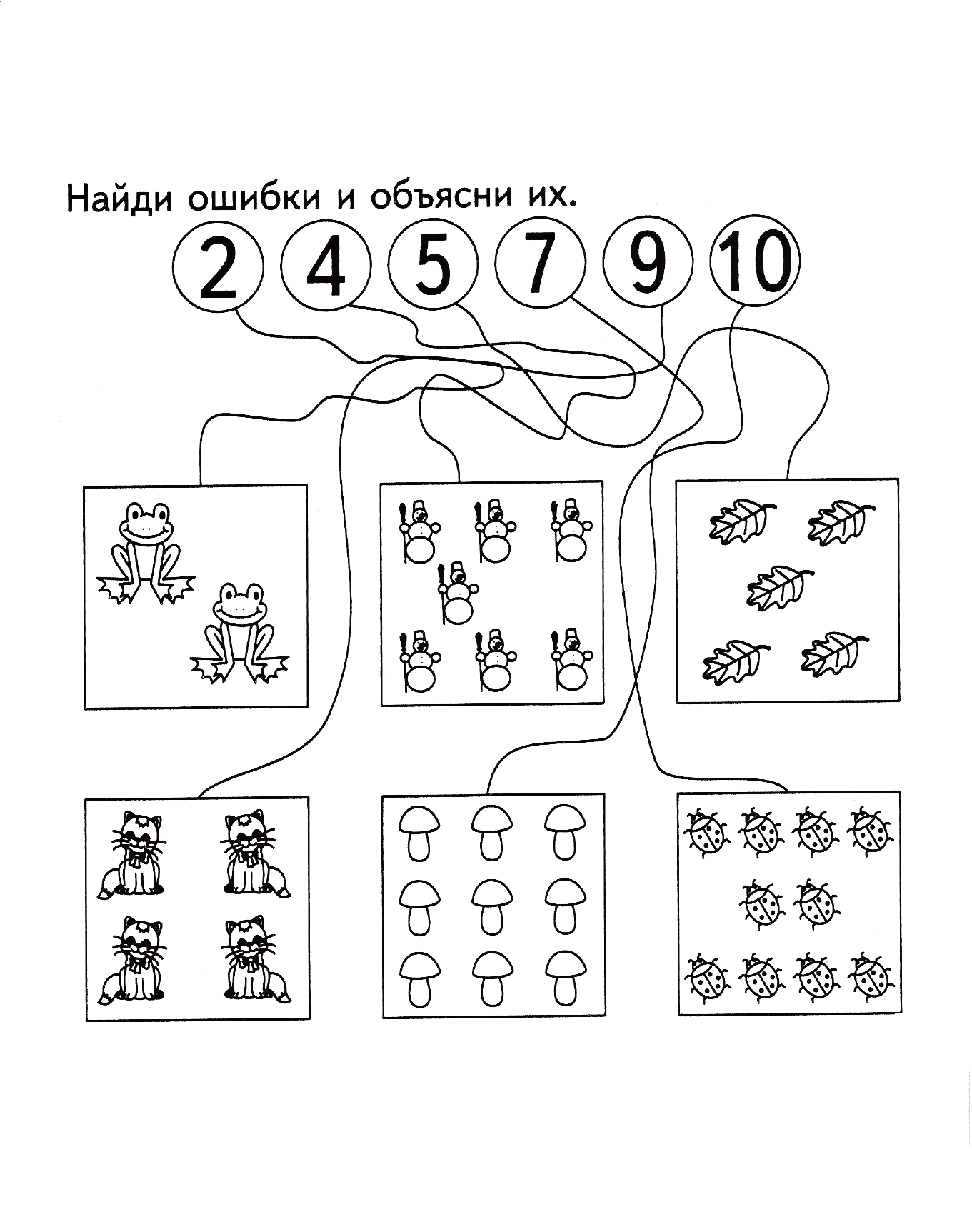
Задание № 6
Количество и счёт
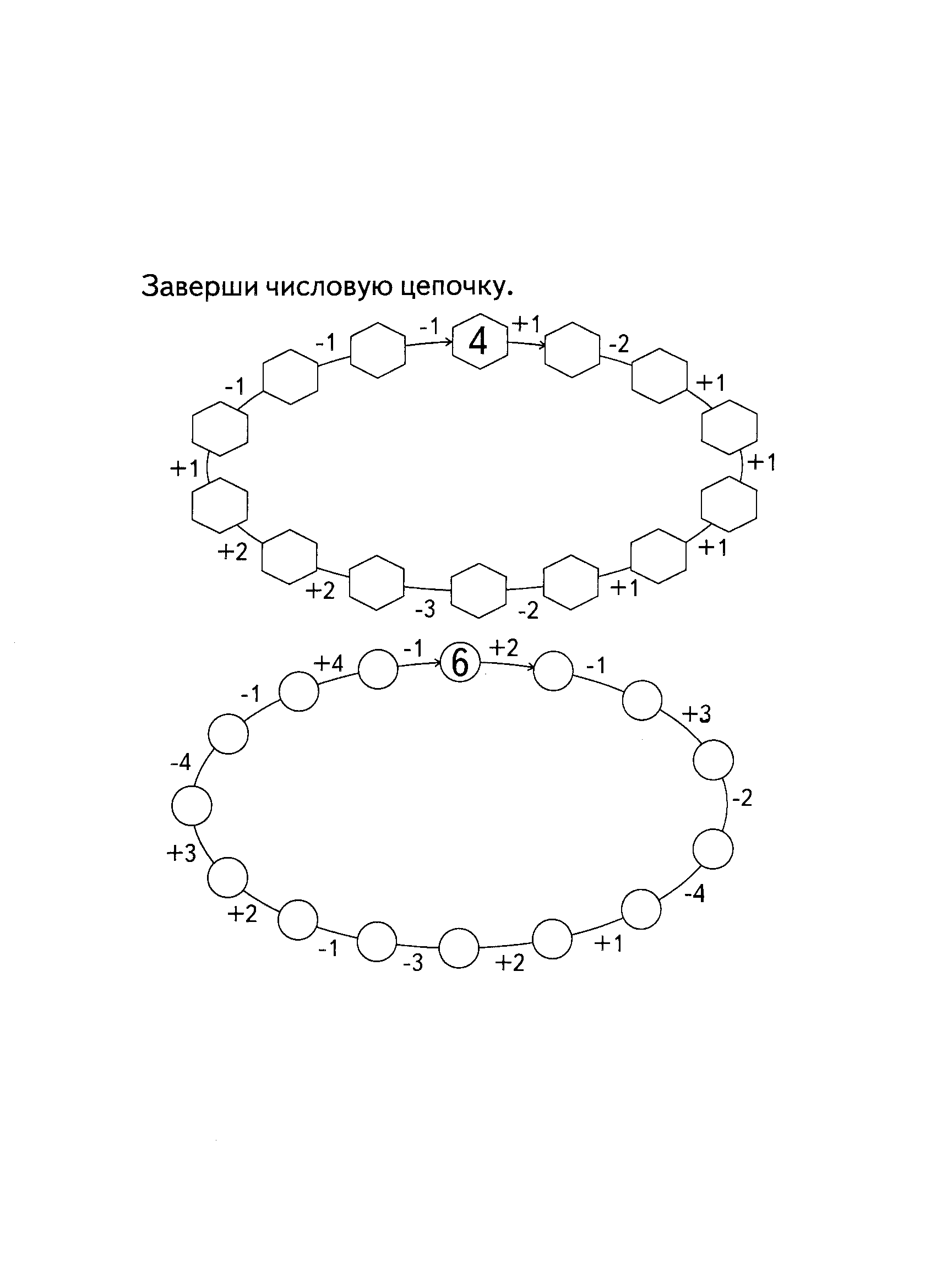
Задание № 7
Количество и счёт
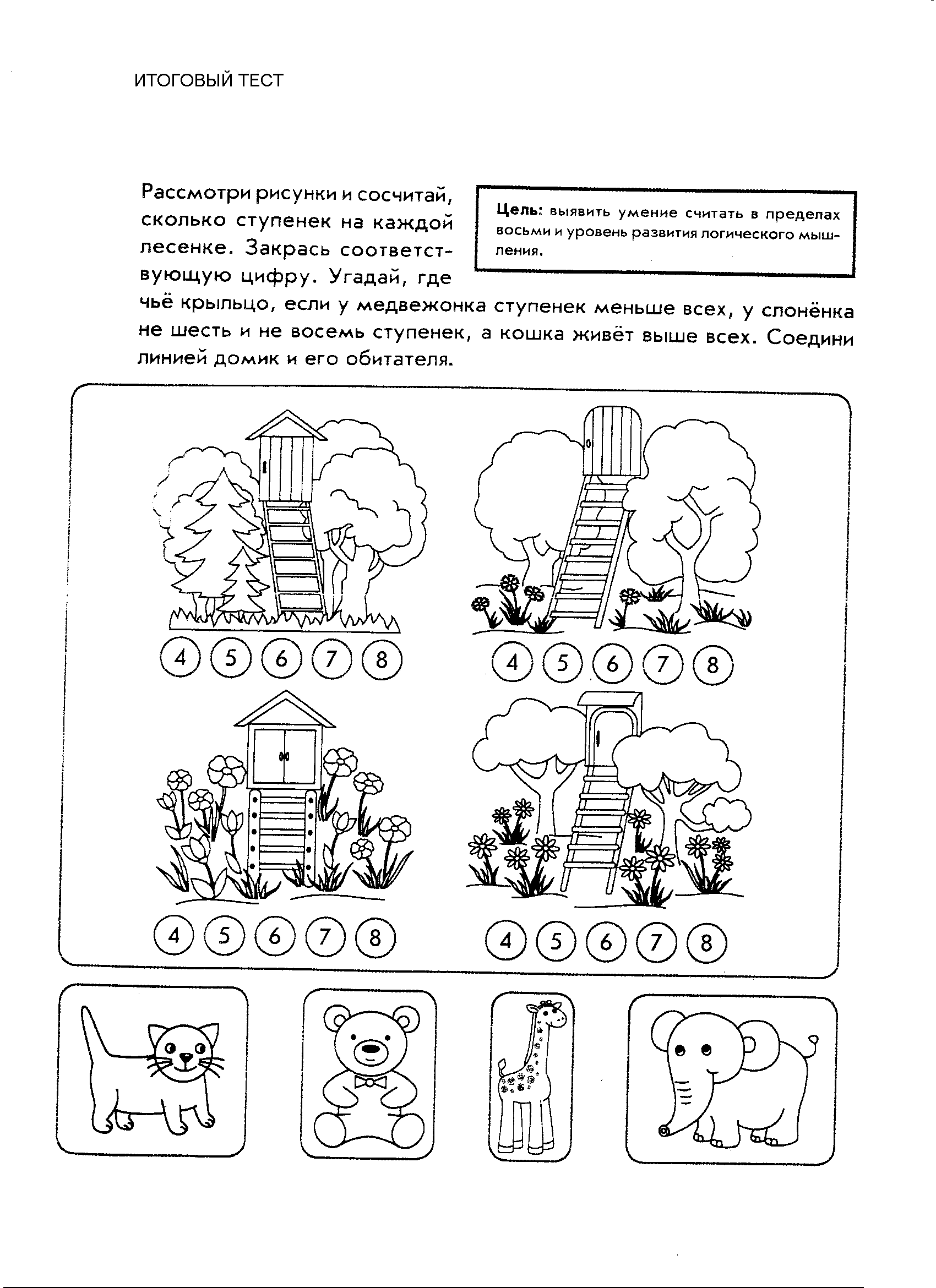
Задание № 8
Геометрические фигуры
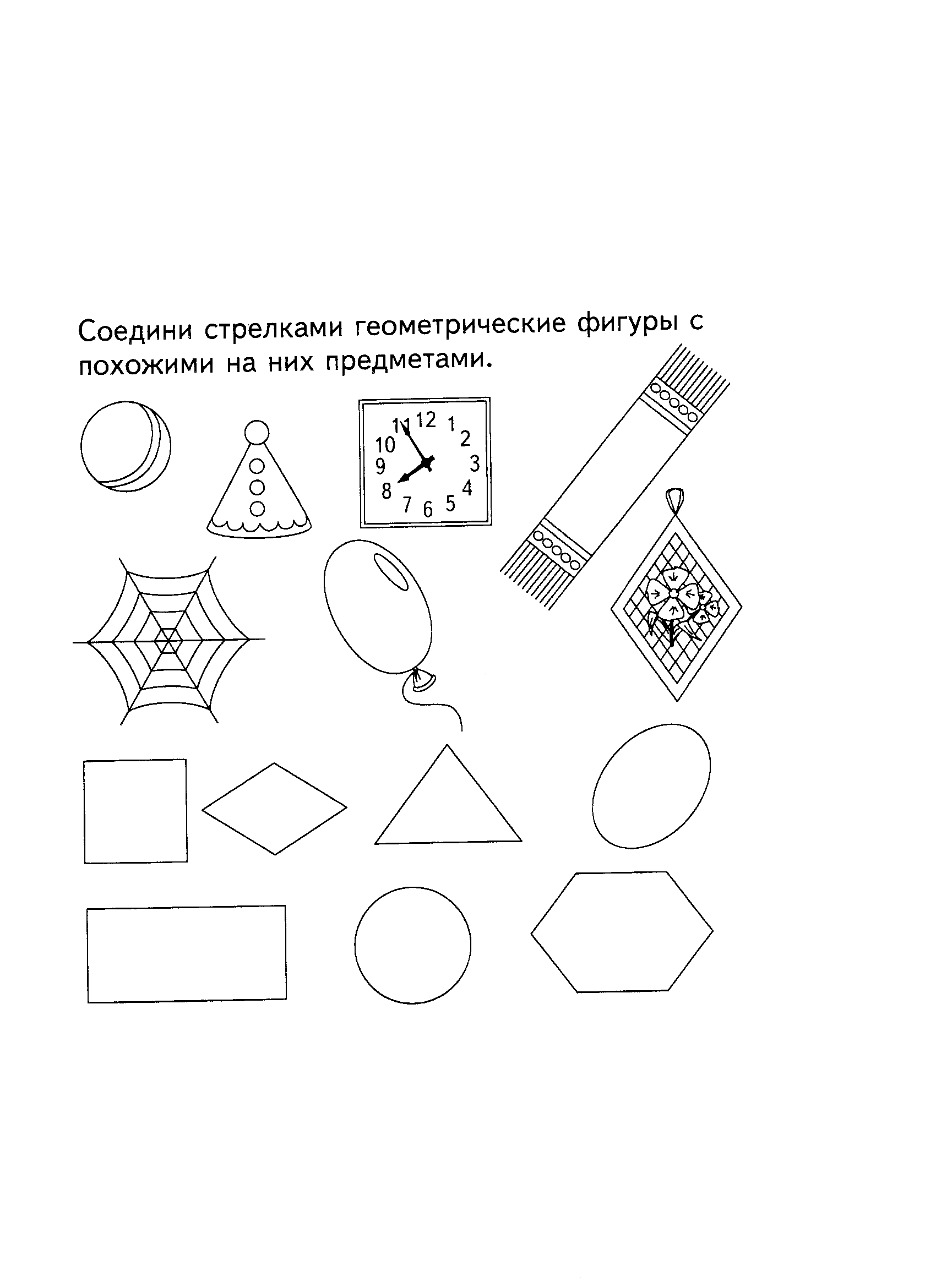
Задание № 9
Геометрические фигуры
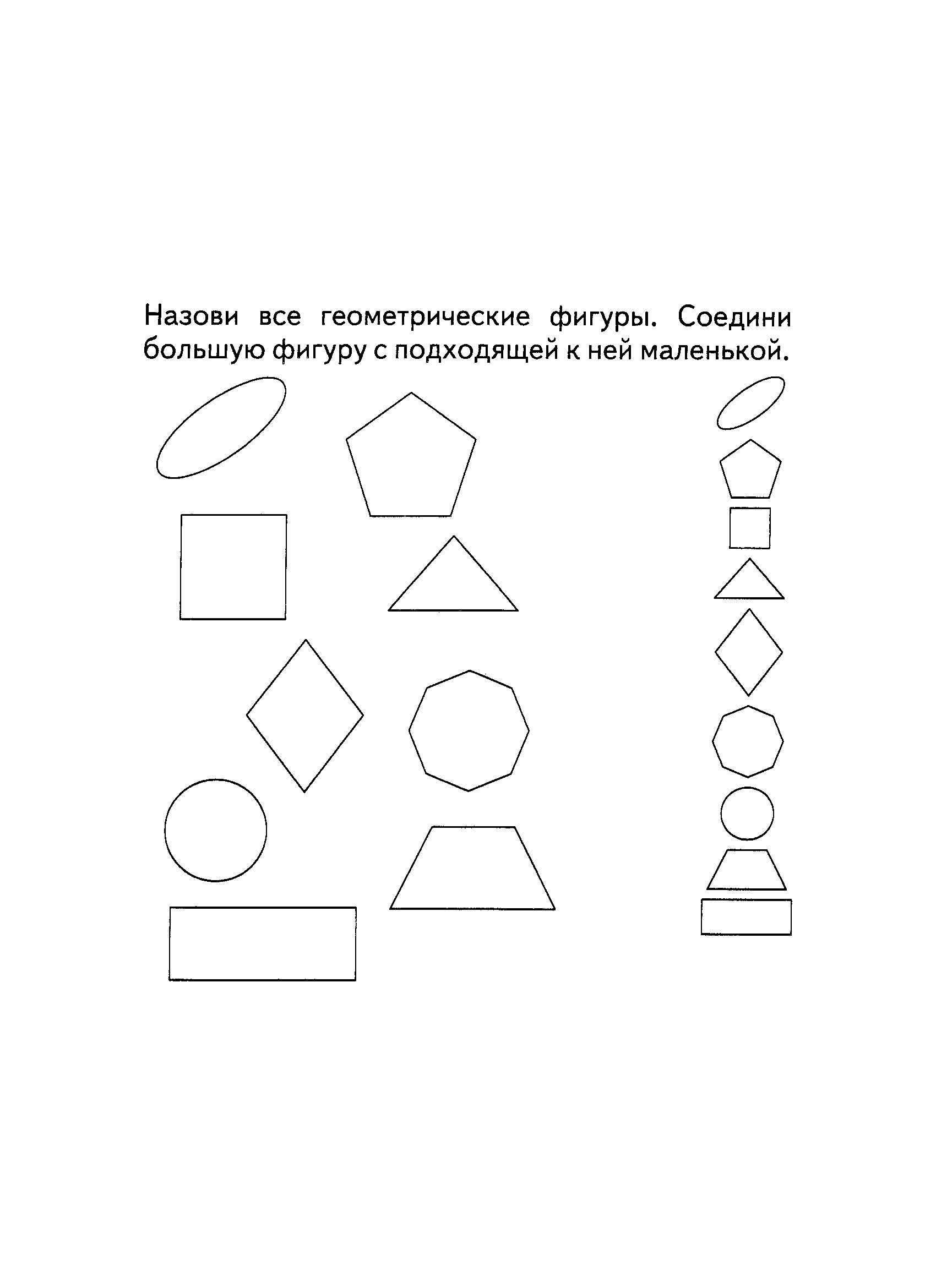
Задание № 10
Ориентировка на плоскости листа
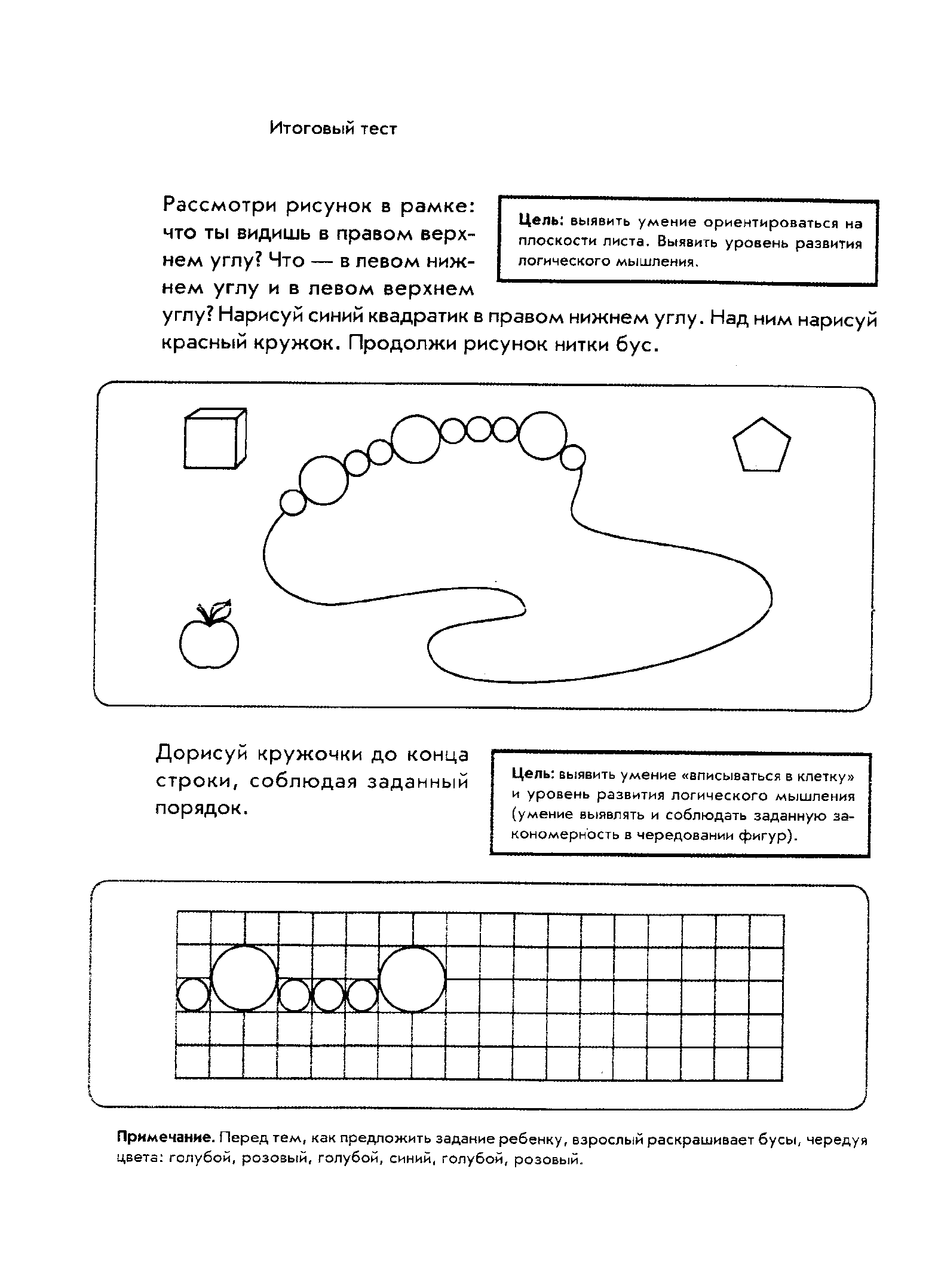
Задание № 11
Пространственные отношения
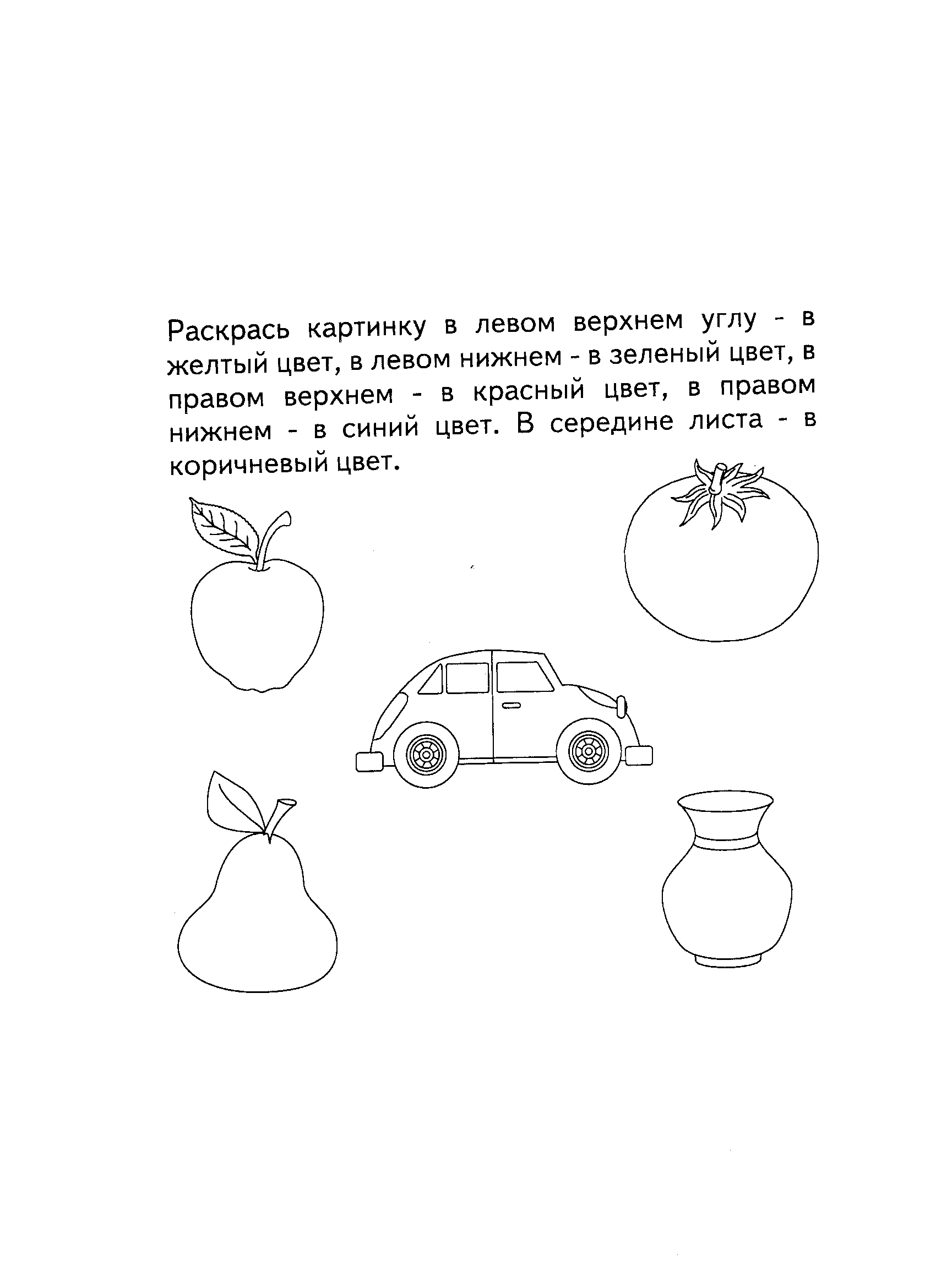
Задание № 12
Измерение длины
Временные отношения
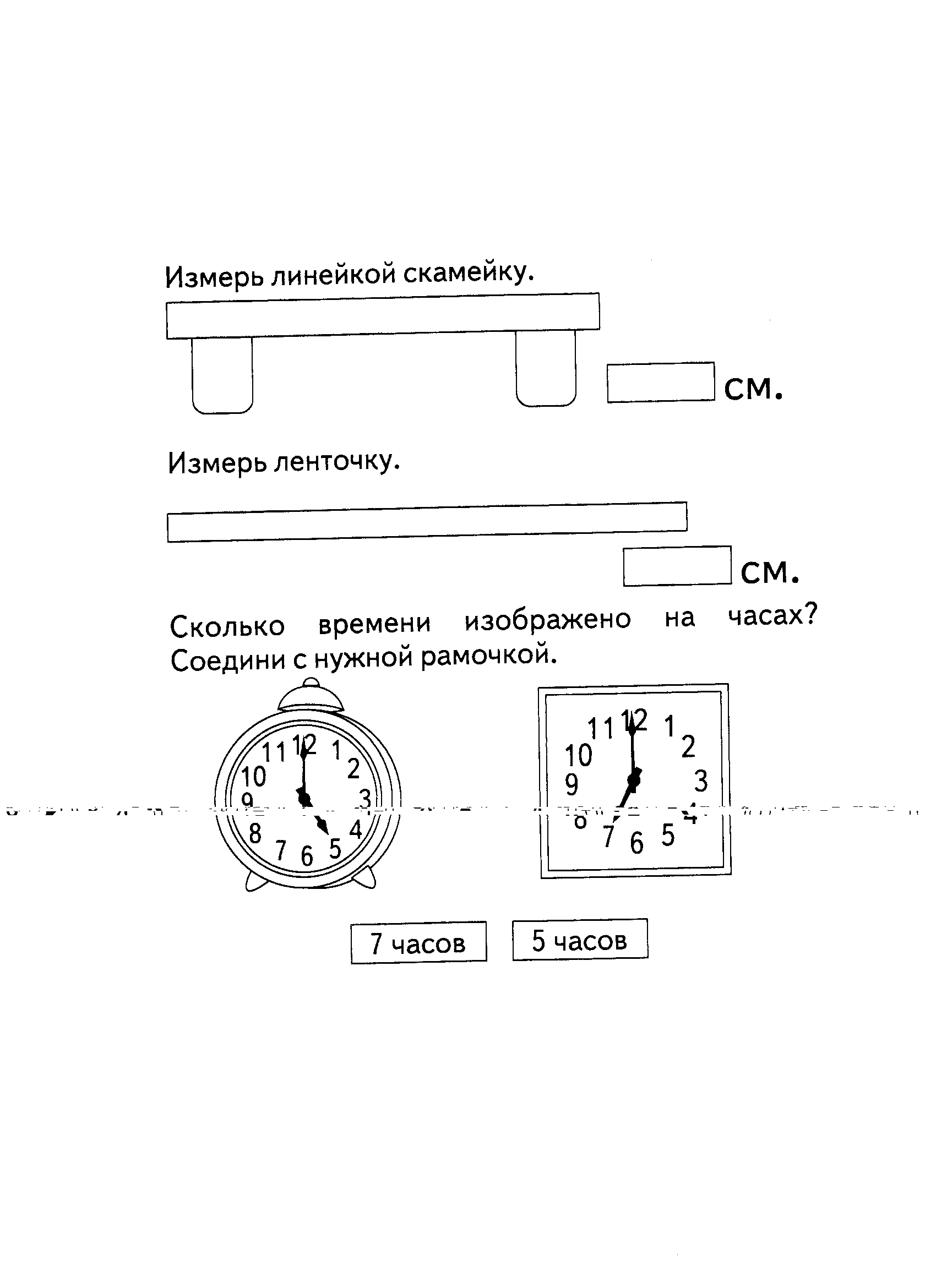
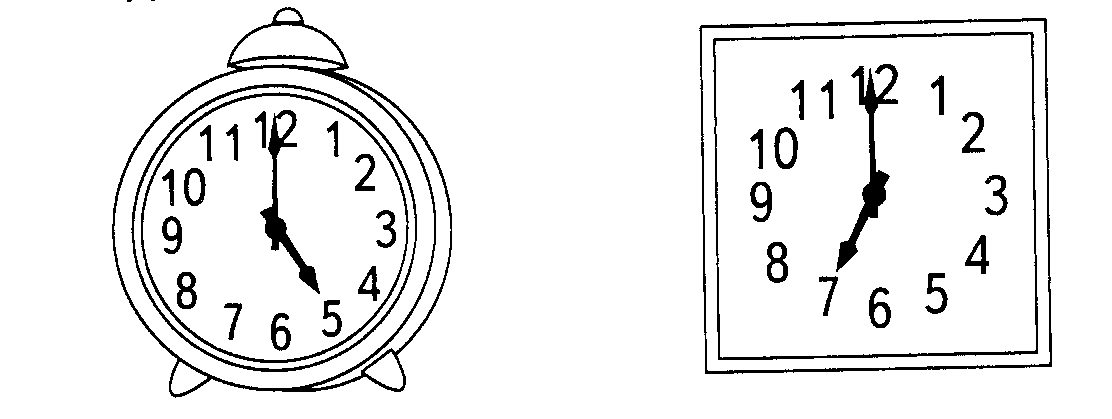

Использованная литература
1. Абрамов И.А. Особенности детского возраста. – М., 1993
2. Аргинская И.И.Математика, математические игры.- Самара: Федоров, 2005 г.- 32 с.
3. Белошистая А. Дошкольный возраст: формирование первичных представлений о натуральных числах // Дошкольное воспитание. – 2002. - №8. – С.30-39
4. Белошистая А.В. Формирование и развитие математических способностей дошкольников. М.: Гуманит. Изд. Центр ВЛАДОС, 2003. 400 с
5. Бильчугов Л.Ф. Формирование элементов формально-логического мышления у детей 6-7 лет. Дис. канд. психолог. наук МГУ., 1978.
6. Игры и упражнения по развитию умственных способностей у детей дошкольного возраста: Кн. для воспитателя дет. сада. – М., 1989
7. Леушина А.М. Формирование математических представлений у детей дошкольного возраста: Учеб .пос. – М., 1974
8. Математическое развитие дошкольников: Учебно-методическое пособие / Сост. З.А. Михайлова, М.Н. Полякова, Р.Л. Непомнящая, А.М. Вербенец.– СПб: Детство-Пресс, 2000.
9. Метлина Л.С. Занятия по математике в детском саду: Формирование у дошкольников элементарных математических представлений. – 2-е изд., доп. – М., 1985
10. Носова Е.А. "Предлогическая подготовка детей дошкольного возраста. Использование игровых методов при формировании у дошкольников математических представлений". - Л.: 1990г. стр.47-62.
11. Петерсон Л.Г., Кочемасова Е.Е. Игралочка: Практическ. курс математики для дошкольников. – М., 2001
12. Сербина Е.В. Математика для малышей: Кн. для воспитателя дет. сада. – М., 1992
13. Шеляховская Н.К., Дацюк Т.Н. О проявлении и развитии математического мышления дошкольников // Резервы познавательной деятельности учащихся и развивающее обучение: Сб. науч. тр. – М., 1990. – С.76 – 86.
14. Эльконин Д.Б. К проблеме периодизации психического развития в детском возрасте //Хрестоматия по возрастной и педагогической психологии. - М., 1991.

| Автор | |
|---|---|
| Дата добавления | 21.10.2019 |
| Раздел | Дошкольная |
| Подраздел | Другое |
| Просмотров | 5285 |
| Номер материала | 6368 |