
Урок "Длина отрезка"

Краткое описание документа:
Видеоурок «Длина отрезка» - наглядное пособие для проведения урока по теме «Длина отрезка». Данное пособие содержит объяснение особенностей операции измерения отрезка, ее смысла. Во время просмотра видеоурока формируется глубокое понимание того, каким образом измеряется отрезок, как формируется значение его длины, особенности представления длины отрезка с различными приближениями.
Подача материала в виде видеоурока предоставляет возможности, которые не дает ни один другой инструмент преподавания – он полностью освобождает учителя от необходимости воспроизводить стандартную информацию и дает возможность сделать акцент в работе учителя на индивидуальный подход. Яркая наглядная анимация облегчает понимание процессов и акцентирует внимание ученика на предмете изучения.
К моменту изучения данной темы ученики уже имеют представление о сравнении геометрических фигур, которое составляет основу операции.
В начале видеоурока объявляется его название и раскрывается смысл длины отрезка как результата его измерения. Новый материал связывается с ранее изученным, отмечая, что процесс измерения отрезков базируется на сравнении их. Вводится понятие единицы измерения в измерении, разъясняется ее геометрический смысл. Измерение длины отрезка представляется как сравнение данного отрезка с единицей измерения. В данном случае предлагается единицей измерения признать сантиметр – отрезок, который будет сравниваться с отрезком, длину которого необходимо измерить. В процессе измерения отрезка определяется, сколько раз можно уложить отрезок в 1 см в данном отрезке. При помощи анимации в видеоуроке хорошо видно, каким образом измеряются отрезки наложением единичного отрезка на его длину. В показанном примере единица измерения уложена в отрезок АС 5 раз, поэтому утверждается, что длина АС равняется 5 см. Математическая запись данного факта определяется как АС=5 см.
Далее рассматриваются случаи, если при укладывании единичного отрезка образуется остаток, который менее единичного отрезка. Каким образом в этом случае определяется длина отрезка? Производится деление отрезка на 10 одинаковых частей, которые помогут представить не укладывающийся в целый единичный отрезок остаток. В качестве примера приводится отрезок АС, длина которого может быть измерена 3 единичными сантиметровыми отрезками, и при этом остается часть, которая меньше сантиметра. В данном остатке помещается 4 малых деления, на которые делится сантиметровый отрезок. Таким образом формируется дробная часть измеренной величины. В этом случае длина АС составляет 3,4 сантиметра.
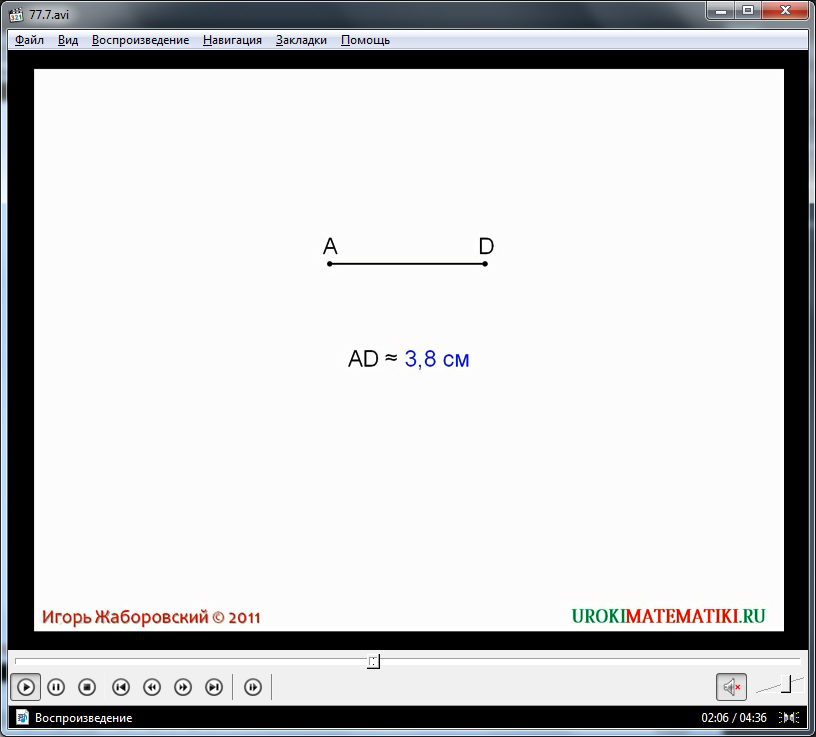
Далее углубляется понятие измерения длина отрезка, рассматривая случай, когда отрезками, на которые делится сантиметр, нельзя точно измерить длину, так как при наложении отрезков тоже есть остаток. Способом указать длину отрезка и учесть оставшуюся часть является указание приближенного значения. На примере отрезка AD показано, когда сантиметровый отрезок накладывается 3 раза, а миллиметровый 8 раз с остатком, длину можно описать как AD≈3,8 см. К тому же подобно делению сантиметрового отрезка на 10 одинаковых частей можно поступить с миллиметровым отрезком и далее, повышая точность измерения.
Обобщая правила измерения отрезков, указывается, что любой отрезок может быть принят условно за единицу измерения, а измеряемый отрезок при накладывании данного отрезка может быть представлен положительным числом. Данное правило выделено на экране в качестве важного вывода. Следующий важный вывод из проделанных операций – при измерении равных отрезков единичные отрезки укладываются одинаковое количество раз, поэтому у равных отрезков одинаковые длины. Данный вывод также отображается на экране и может быть записан учениками для закрепления материала. Также делается вывод об измерении различных отрезков – если один из отрезков меньше второго, то в него укладывается меньшее число единичных отрезков. Как следствие этого, можно утверждать, что меньший отрезок соответственно имеет меньшую длину. Данный вывод отображается на экране и может быть предложен для записи учениками.
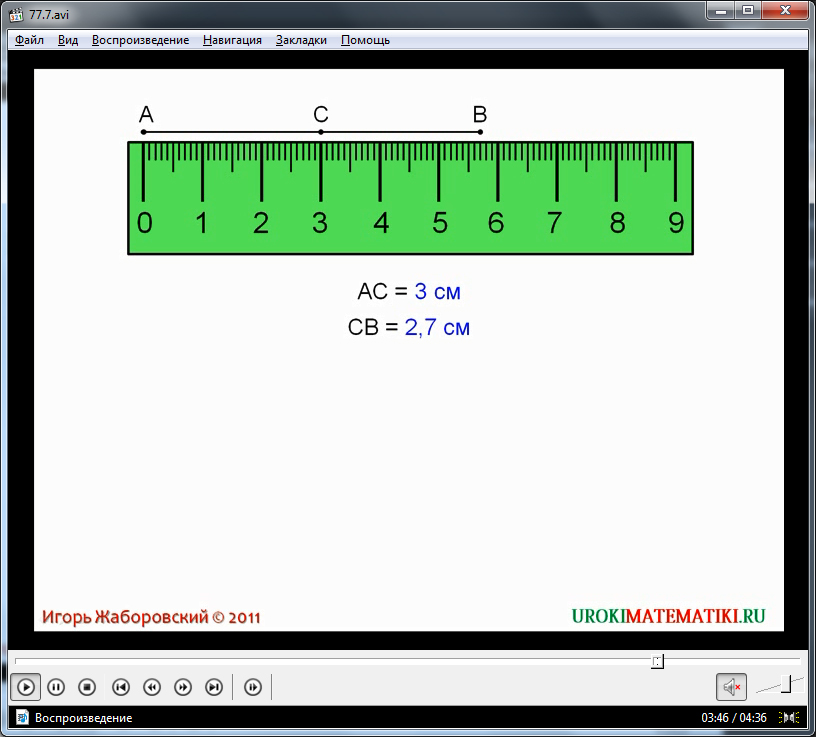
Важной особенностью измерения длины отрезка, которая лежит в основе решения многих геометрических задач, является равенство длины отрезка сумме длин его частей, на которые он разбивается любой его точкой. Предлагается рассмотреть отрезок АВ, который разделен точкой С. При этом измеряется длина первого образованного в результате разбиения отрезка АС, которая равна 3 см. Длина второго получившегося отрезка СВ равна 2,7 см. Общая измеренная длина отрезка АВ – 5,7 см. Очевидно, что длина отрезка АВ может быть представлена суммой длин составляющих его частей. На экране располагается математическая запись данного факта АВ=АС+СВ. переходя от частного случая к общему делается вывод о том, что при делении отрезка точкой на две части, его длина будет равной сумме образованных отрезков.
Также ученикам предлагается обратить внимание на случай, когда длина отрезка CD больше длины отрезка АВ в kраз. На экране показывается математическая запись этого случая CD= k·АВ. В конце видеоурока описывается физический смысл длины отрезка – она представляется как расстояние между его концами.
Видеоурок «Длина отрезка» может быть использован учителем на уроке геометрии для замены живой подачи нового материала работой технических средств. Подробное и понятное видеообъяснение станет хорошим инструментом для дистанционного обучения или самостоятельного изучения материала учеником.
| Автор | |
|---|---|
| Дата добавления | 02.08.2014 |
| Раздел | Геометрия |
| Подраздел | Видеоурок |
| Просмотров | 5731 |
| Номер материала | 494 |