
Исследовательская работа ученицы 9"А" класса по теме: "Вневписанная окружность"


















Описание презентации по отдельным слайдам:
Областной конкурс «Взлёт» исследовательских проектов обучающихся образовательных организаций Самарской области «Вневписанная окружность» Работу выполнила: Мусаева Анастасия Валериевна, ученица 9А класса ГБОУ СОШ №2 «ОЦ» с. Кинель – Черкассы Руководитель: учитель математики первой категории Лукьянова Ольга Владимировна Консультант: кандидат наук ФГБОУ ВО СамГТУ Фадеева Оксана Владиславовна
Игорь Фёдорович Шарыгин: «Каждый треугольник определяет семейство окружностей, помогающих глубже и полнее понять "устройство" треугольника"
Цель: сформировать представление о вневписанной окружности и её практической значимости. Задачи: -ввести определение вневписанной окружности треугольника; -изучить свойства вневписанной окружности и её связь с основными элементами треугольника; -применить свойства вневписанной окружности при решении задач на доказательство, построение и вычисление.
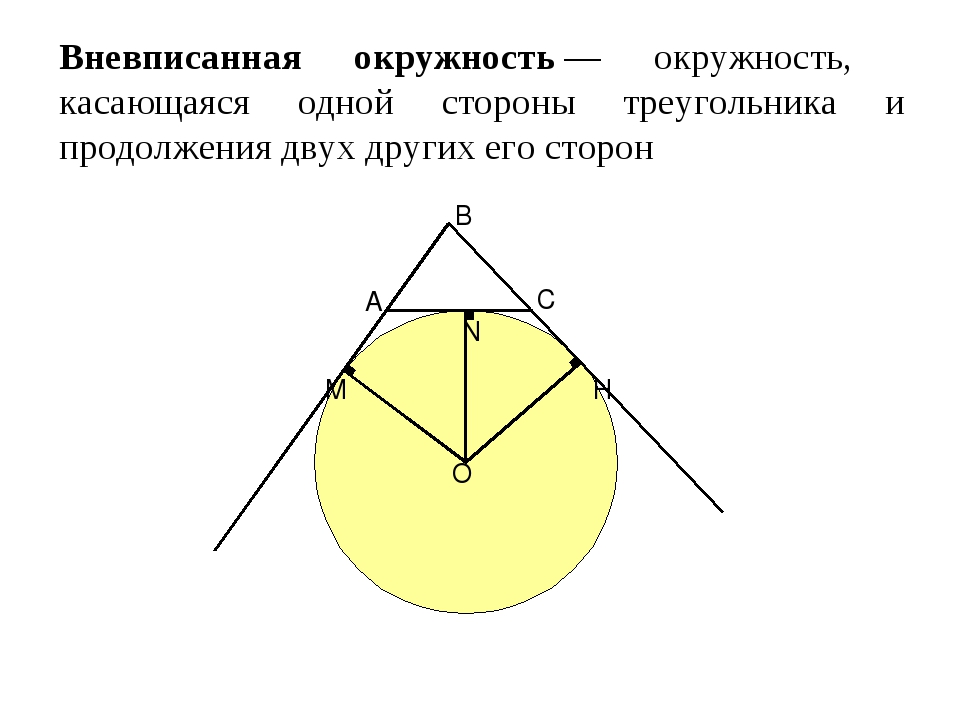
Вневписанная окружность — окружность, касающаяся одной стороны треугольника и продолжения двух других его сторон М N H
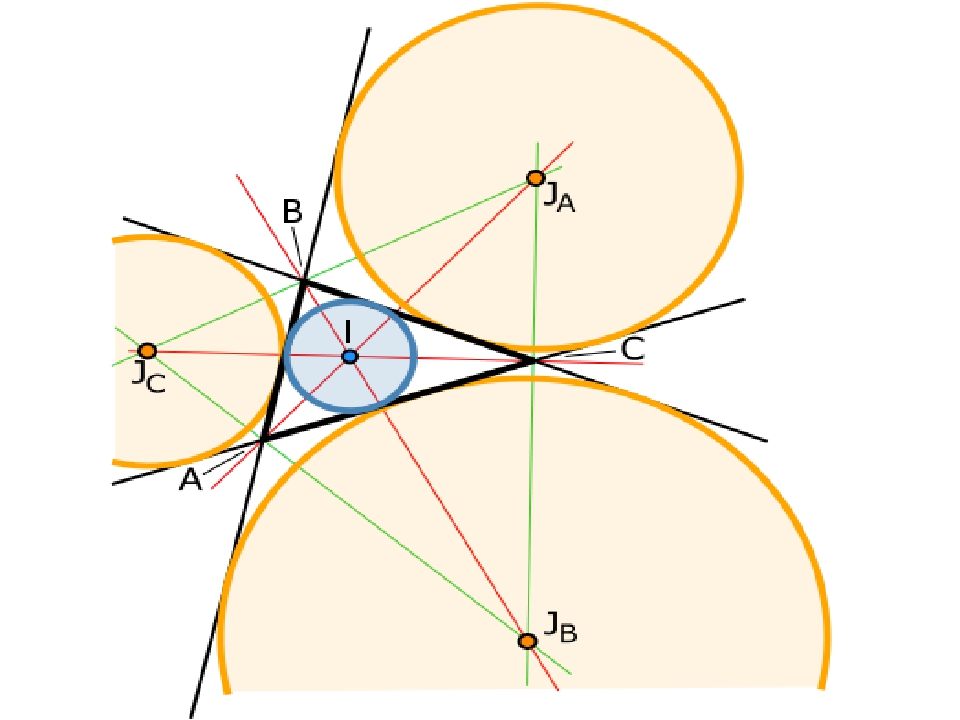
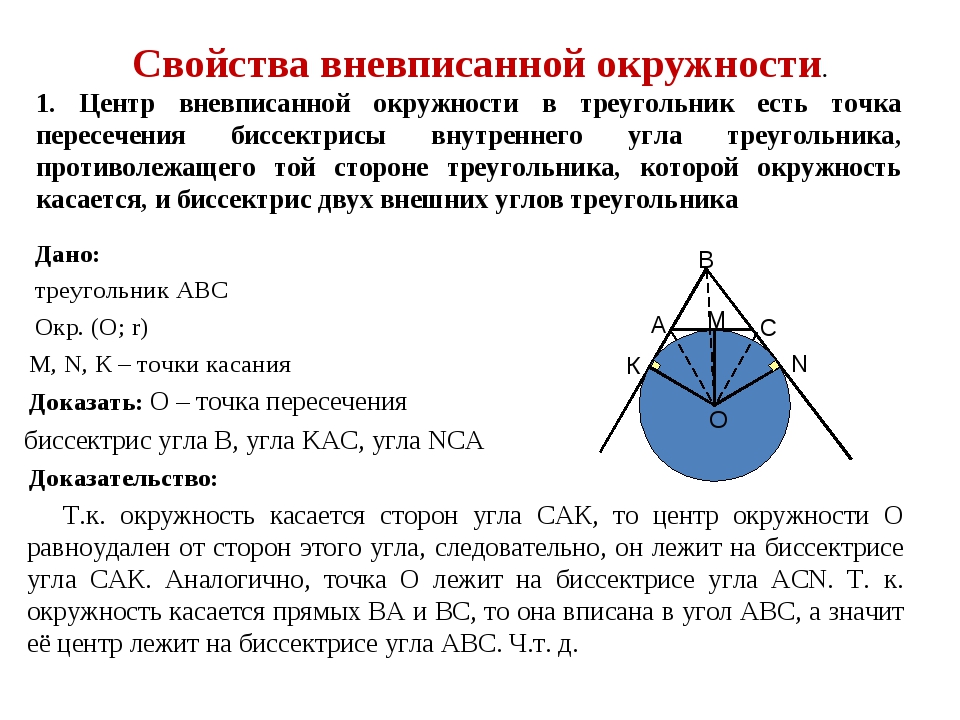
Свойства вневписанной окружности. Дано: треугольник АВС Окр. (О; r) М, N, К – точки касания Доказать: О – точка пересечения биссектрис угла B, угла KAC, угла NCA Доказательство: Т.к. окружность касается сторон угла САК, то центр окружности О равноудален от сторон этого угла, следовательно, он лежит на биссектрисе угла САК. Аналогично, точка О лежит на биссектрисе угла АСN. Т. к. окружность касается прямых ВА и ВС, то она вписана в угол АВС, а значит её центр лежит на биссектрисе угла АВС. Ч.т. д. 1. Центр вневписанной окружности в треугольник есть точка пересечения биссектрисы внутреннего угла треугольника, противолежащего той стороне треугольника, которой окружность касается, и биссектрис двух внешних углов треугольника
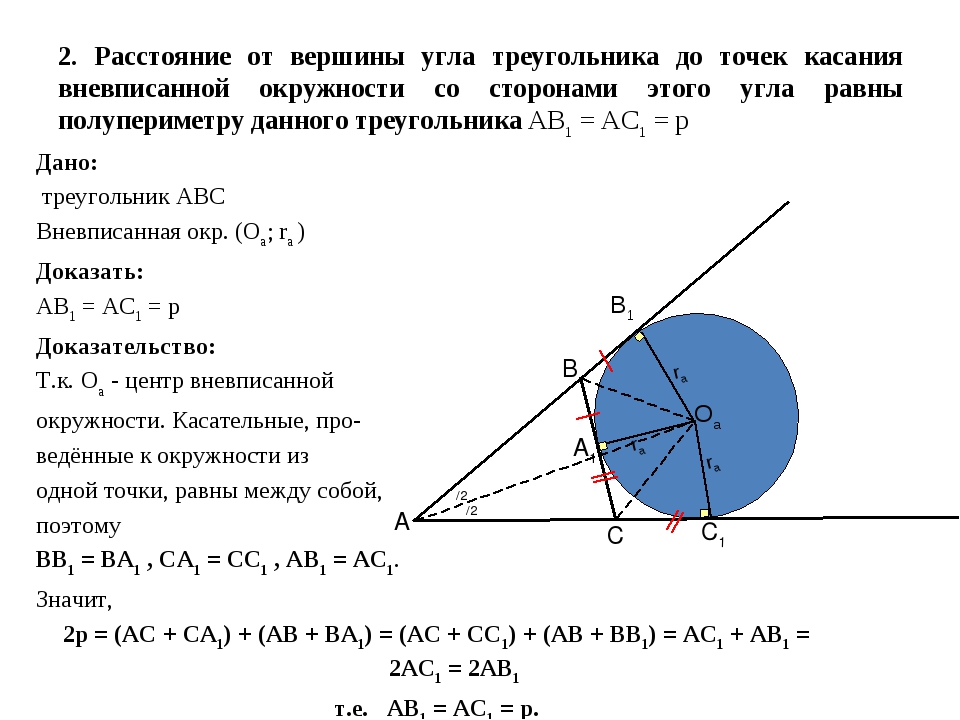
2. Расстояние от вершины угла треугольника до точек касания вневписанной окружности со сторонами этого угла равны полупериметру данного треугольника АВ1 = АС1 = p Дано: треугольник АВС Вневписанная окр. (Оа; ra ) Доказать: АВ1 = АС1 = p Доказательство: Т.к. Оа - центр вневписанной окружности. Касательные, про- ведённые к окружности из одной точки, равны между собой, поэтому ВВ1 = ВА1 , СА1 = СС1 , АВ1 = АС1. Значит, 2p = (AC + СА1) + (AB + ВА1) = (AC + CC1) + (AB + BB1) = AC1 + AB1 = 2AC1 = 2AB1 т.е. АВ1 = АС1 = p. Оа В1 ra ra ra А В С С1 А1 α/2 α/2
1. Радиус вневписанной окружности. Касающейся сторон данного внутреннего угла треугольника, равен произведению полупериметра треугольника на тангенс половины этого угла, т. е. ra = ptg , rb = ptg , rc = ptg Дано: треугольник АВС Вневписанная окр. (Оа ; ra) Доказать: r a = p * tg * Доказательство: В прямоугольном треугольнике А Оа С1 ra и p – длины катетов, угол Оа А С1 равен , поэтому ra = ptg . А В С Оа p p В1 С1 b c ra ra ra Некоторые соотношения с радиусами вневписанных окружностей
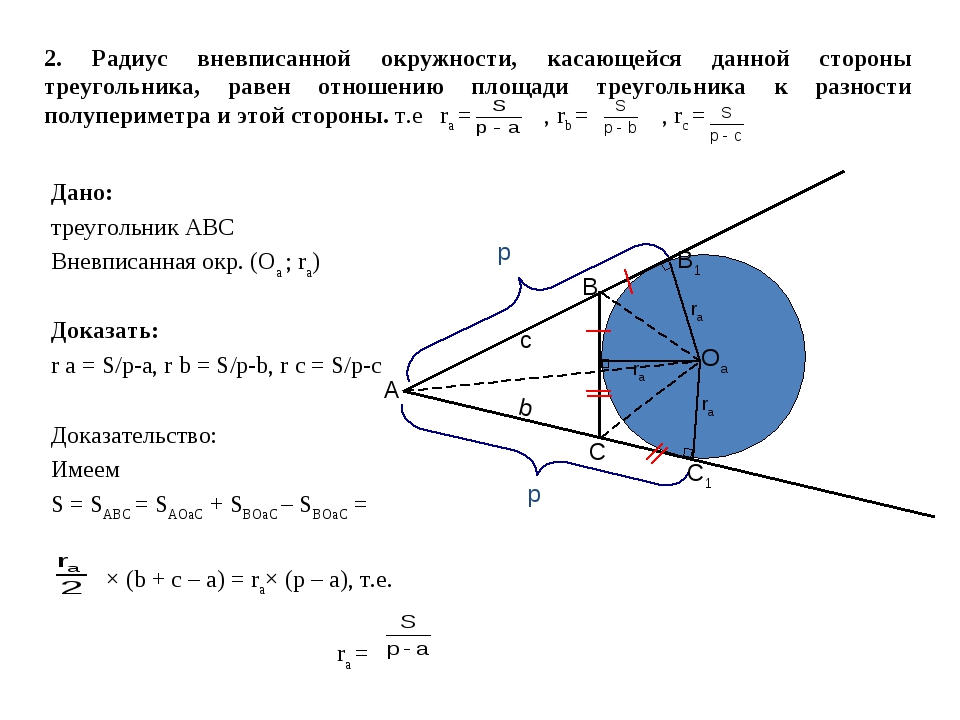
2. Радиус вневписанной окружности, касающейся данной стороны треугольника, равен отношению площади треугольника к разности полупериметра и этой стороны. т.е ra = , rb = , rc = Дано: треугольник АВС Вневписанная окр. (Оа ; ra) Доказать: r a = S/p-a, r b = S/p-b, r c = S/p-c Доказательство: Имеем S = SABC = SAOaC + SBOaC – SBOaC = × (b + c – a) = ra× (p – a), т.е. ra = А В С Оа p p В1 С1 b c ra ra ra
3. Сумма радиусов вневписанных окружностей равна сумме радиуса вписанной окружности и удвоенного диаметра описанной окружности, т. е. ra + rb + rc = r + 4R
4. Сумма величин, обратных радиусам вневписанных окружностей, равна величине, обратной радиусу вписанной окружности, т. е. Доказательство: Используем выражения радиусов через стороны и площадь треугольника: r = , R = , ra = , rb = , rc = Значит,
5. Сумма всех попарных произведений радиусов вневписанных окружностей равна квадрату полупериметра треугольника, т. е. rarb + rbrc + rcra = p2 Доказательство:
6.Произведение всех трех радиусов вневписанных окружностей равно произведению радиуса вписанной окружности на квадрат полупериметра треугольника, т.е. rarbrc = rp2 Доказательство: Из ранее доказанных формул для радиусов и формулы Герона ra = , rb = , rc = , Тогда
Следствие 1. Площадь треугольника равна отношению произведения всех трех радиусов вневписанных окружностей к полупериметру треугольника, т.е. Доказательство: Из rarbrc = rp2 = rp × p = Sp. Следовательно
Следствие 2. Площадь треугольника равна квадратному корню из произведения всех трех радиусов вневписанных окружностей и радиуса вписанной окружности, т.е. Доказательство: Из следствия 1, что и равенства S = pr, получаем, перемножая их почленно, . Значит
Следствие 3. Величина, обратная высоте треугольника, опущенной на его данную сторону, равна полусумме величин, обратных радиусам вневписанных окружностей, касающихся двух других сторон треугольника, т.е. , , Доказательство: Воспользуемся формулами , Значит, ,
Применение свойств вневписанных окружностей при решении задач Задача 1. В треугольнике АВС проведены биссектрисы AD и ВЕ. DЕ – биссектриса угла ADC. Найдите величину угла А Решение: Точка Е равноудалена от прямых AD,BC и АВ, поскольку она лежит на биссектрисах DE и ВЕ углов ADC и АВС. Значит, Е – центр вневписанной окружности тр. ADB. AD - биссектриса угла BAC = Лучи АЕ и AD делят развернутый угол с вершиной А на три равных угла. Следовательно, каждый из них равен 60 градусов, а угол BAC = 120 градусов
Задача 2. К двум непересекающимся окружностям проведены две общие внешние касательные и общая внутренняя касательная. Докажите, что отрезок внутренней касательной, заключенной между внешними касательными, равен отрезку внешней касательной, заключенному между точками касания. Доказательство. Пусть MN = а. АК = р, тогда ВК = р-а. Значит, АВ = p – (p – a) = а, То есть АВ = MN. Аналогично доказываются, что CD = MN.
Задачи ОГЭ и ЕГЭ на применение свойств вневписанных окружностей. ЗАДАЧА №1 (сборник «Подготовка к ЕГЭ-2010, под редакцией Ф.Ф.Лысенко) «Найдите произведение радиусов всех вневписанных окружностей треугольника со сторонами 4,5,6». ЗАДАЧА №2 (сборник «Подготовка к ЕГЭ-2010, под редакцией Ф.Ф.Лысенко) «Найдите произведение сторон треугольника, если известно, что радиусы его вневписанных окружностей равны 9,18 и 21». ЗАДАЧА №3 (сборник «Подготовка к ОГЭ-2018», под редакцией Д.А. Мальцева) «Основание АС равнобедренного треугольника равно 10. Окружность радиуса 7,5 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания АС в его середине. Найдите радиус окружности вписанной в треугольник АВС».
ЗАДАЧА №4 « Найдите радиус вневписанной окружности треугольника, если радиусы двух других вневписанных окружностей равны 2002 и 4004, а радиус вписанной окружности равен 1001». ЗАДАЧА №5. (Сборник « Математика. Все для ЕГЭ 2018». Часть I. Автор Д. А. Мальцев) « Точка О1 - центр вписанной окружности треугольника АВС, а точка О2 – центр окружности, касающейся стороны ВС и продолжений сторон АВ и АС. Найдите расстояние между точками О1 и О2 , если радиус описанной окружности треугольника АВС равен 6, а sin ∟ВО1С = √5/3.
Заключение. Изящество и красота применения окружности создают ощущение элитарности. В учебнике «Геометрия 7-9» автора И. Ф. Шарыгина окружностям уделяется большое внимание. К сожалению, во многих учебниках этой фигуре уделяется незначительное время и внимание, а про вневписанную окружность и не упоминается. Поэтому я считаю, что мою работу можно использовать на уроках геометрии при рассмотрении темы «Вписанные и описанные окружности»

| Автор | |
|---|---|
| Дата добавления | 26.05.2019 |
| Раздел | Геометрия |
| Подраздел | Научная работа |
| Просмотров | 4597 |
| Номер материала | 6226 |