
Конспект урока "Динамическое программирование"
1. Динамическое программирование
Задача динамического программирования
Большинство методов исследования операций связано в первую очередь с задачами вполне определенного содержания. Классический аппарат математики оказался малопригодным для решения многих задач оптимизации, включающих большое число переменных и/или ограничений в виде неравенств. Несомненна привлекательность идеи разбиения задачи большой размерности на подзадачи меньшей размерности, включающие всего по нескольких переменных, и последующего решения общей задачи по частям. Именно на этой идее основан метод динамического программирования.
Динамическое программирование (ДП) представляет собой математический метод, заслуга создания и развития которого принадлежит, прежде всего, Беллману. Метод можно использовать для решения весьма широкого круга задач, включая задачи распределения ресурсов, замены и управления запасами, задачи о загрузке. Характерным для динамического программирования является подход к решению задачи по этапам, с каждым из которых ассоциирована одна управляемая переменная. Набор рекуррентных вычислительных процедур, связывающих различные этапы, обеспечивает получение допустимого оптимального решения задачи в целом при достижении последнего этапа.
Происхождение названия динамическое программирование, вероятно, связано с использованием методов ДП в задачах принятия решений через фиксированные промежутки времени (например, в задачах управления запасами). Однако методы ДП успешно применяются также для решения задач, в которых фактор времени не учитывается. По этой причине более удачным представляется термин многоэтапное программирование, отражающий пошаговый характер процесса решения задачи.
Фундаментальным принципом, положенным в основу теории ДП, является принцип оптимальности. По существу, он определяет порядок поэтапного решения допускающей декомпозицию задачи (это более приемлемый путь, чем непосредственное решение задачи в исходной постановке) с помощью рекуррентных вычислительных процедур.
Динамическое программирование позволяет осуществлять оптимальное планирование управляемых процессов. Под «управляемыми» понимаются процессы, на ход которых мы можем в той или другой степени влиять.
Пусть предполагается к осуществлению некоторое мероприятие или серия мероприятий («операция»), преследующая определенную цель. Спрашивается: как нужно организовать (спланировать) операцию для того, чтобы она была наиболее эффективной? Для того, чтобы поставленная задача приобрела количественный, математический характер, необходимо ввести в рассмотрение некоторый численный критерий W, которым мы будем характеризовать качество, успешность, эффективность операции. Критерий эффективности в каждом конкретном случаи выбирается исходя из целевой направленности операции и задачи исследования (какой элемент управления оптимизируется и для чего).
Сформулируем общий принцип, лежащий в основе решения всех задач динамического программирования («принцип оптимальности»):
«Каково бы ни было состояние системы S перед очередным шагом, надо выбрать управление на этом шаге так, чтобы выигрыш на данном шаге плюс оптимальный выигрыш на всех последующих шагах был максимальным».
Динамическое программирование – это поэтапное планирование многошагового процесса, при котором на каждом этапе оптимизируется только один шаг. Управление на каждом шаге должно выбираться с учетом всех его последствий в будущем.
При постановке задач динамического программирования следует руководствоваться следующими принципами:
Выбрать параметры (фазовые координаты), характеризующие состояние S управляемой системы перед каждым шагом.
Расчленить операцию на этапы (шаги).
Выяснить набор шаговых управлений xi для каждого шага и налагаемые на них ограничения.
Определить какой выигрыш приносит на i-ом шаге управление xi, если перед этим система была в состоянии S, т.е. записать «функцию выигрыша»:
![]() .
.
Определить, как изменяется состояние S системы S под влиянием управление xi на i-ом шаге: оно переходит в новое состояние
![]() . (1.1)
. (1.1)
Записать основное рекуррентное уравнение динамического программирования, выражающее условный оптимальный выигрыш Wi(S) (начиная с i-го шага и до конца) через уже известную функцию Wi+1(S):
![]() . (1.2)
. (1.2)
Этому выигрышу соответствует условное оптимальное управление на i-м шаге xi(S) (причем в уже известную функцию Wi+1(S) надо вместо S подставить измененное состояние ![]() )
)
Произвести условную оптимизацию последнего (m-го) шага, задаваясь гаммой состояний S, из которых можно за один шаг дойти до конечного состояния, вычисляя для каждого из них условный оптимальный выигрыш по формуле
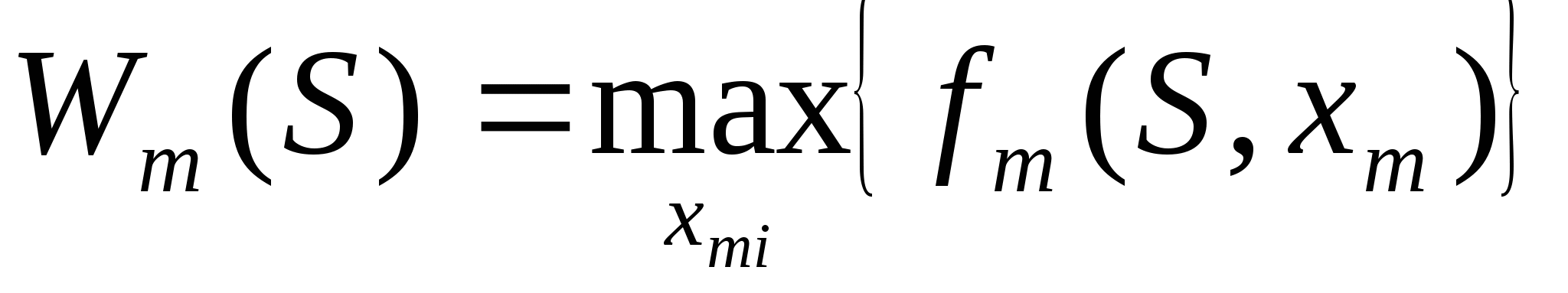
Произвести условную оптимизацию (m-1)-го, (m-2)-го и т.д. шагов по формуле (1.2), полагая в ней i=(m-1),(m-2),…, и для каждого из шагов указать условное оптимальное управление xi(S), при котором максимум достигается.
Заметим, что если состояние системы в начальный момент известно (а это обычно бывает так), то на первом шаге варьировать состояние системы не нужно - прямо находим оптимальный выигрыш для данного начального состояния S0. Это и есть оптимальный выигрыш за всю операцию
![]()
Произвести безусловную оптимизацию управления, «читая» соответствующие рекомендации на каждом шаге. Взять найденное оптимальное управление на первом шаге
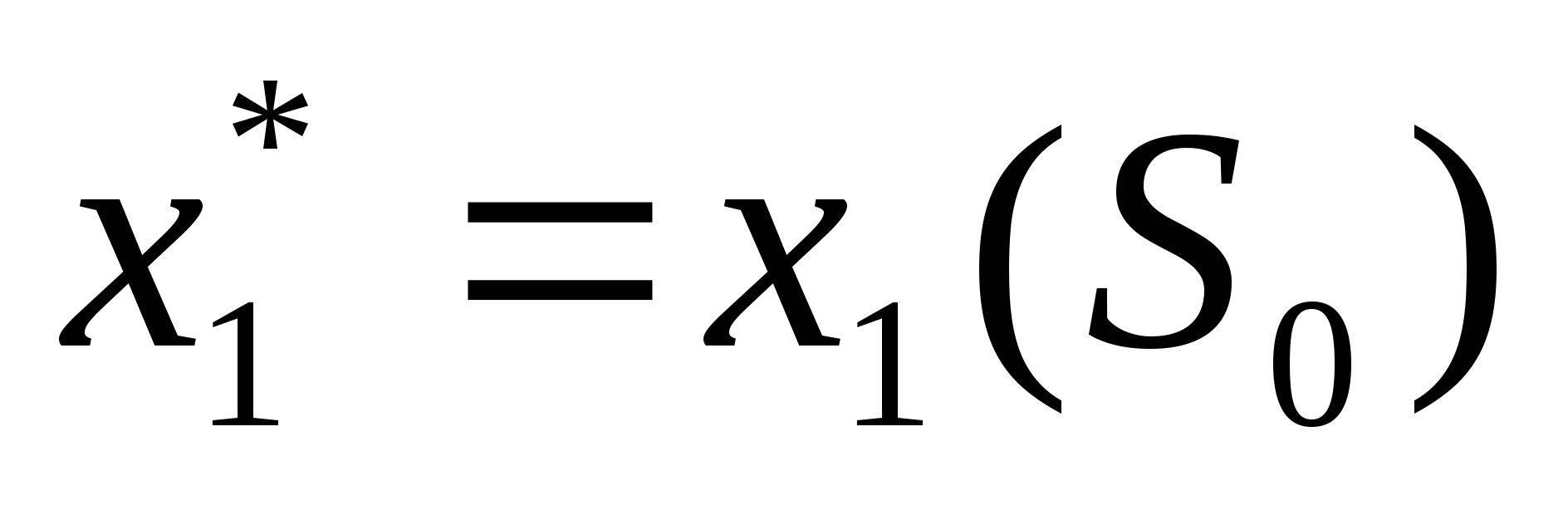 ; изменить состояние системы по формуле (1.1); для вновь найденного состояния найти оптимальное управление на втором шаге х2* и т.д. до конца.
; изменить состояние системы по формуле (1.1); для вновь найденного состояния найти оптимальное управление на втором шаге х2* и т.д. до конца.
Данные этапы рассматривались для аддитивных задач, в которых выигрыш за всю операцию равен сумме выигрышей на отдельных шагах. Метод динамического программирования применим также и к задачам с так называемым «мультипликативным» критерием, имеющим вид произведения:
![]()
(если только выигрыши wi положительны). Эти задачи решаются точно так же, как задачи с аддитивным критерием, с той единственной разницей, что в основном уравнении (1.2) вместо знака «плюс» ставится знак «умножения»:
![]()
Задача о загрузке.
Задача о загрузке – это задача о рациональной загрузке судна (самолета, автомашины и т.п.), которое имеет ограничения по объему или грузоподъемности. Каждый помещенный на судно груз приносит определенную прибыль. Задача состоит в определении загрузки судна такими грузами, которые приносят наибольшую суммарную прибыль.
Рекуррентное уравнение процедуры обратной прогонки выводится для общей задачи загрузки судна грузоподъемностью W предметов (грузов) n наименований. Пусть mi-количество предметов і-го наименования, подлежащих загрузке, ri-прибыль, которую приносит один загруженный предмет і-го наименования, wi-вес одного предмета і-го наименования. Общая задача имеет вид следующей целочисленной задачи линейного программирования.
Максимизировать z=r1m1+r2m2+…+rnmn.
при условии, что
w1m1+w2m2+…+wnmn ![]() W,
W,
m1,m2,…,mn ![]() 0 и целые.
0 и целые.
Три элемента модели динамического программирования определяются следующим образом:
Этап і ставится в соответствии предмету і-го наименования, і=1,2,…n.
Варианты решения на этапе і описываются количеством mi предметов і-го наименования, подлежащих загрузке. Соответствующая прибыль равна rimi. Значение mi заключено в пределах от 0 до [W/wi], где [W/wi] – целая часть числа W/wi.
Состояние xi на этапе і выражает суммарный вес предметов, решения о погрузке которых приняты на этапах і,і+1,...n. Это определение отражает тот факт, что ограничения по весу является единственным, которое связывает n этапов вместе.
Пусть fi(xi)-максимальная суммарная прибыль от этапов і,і+1,...,n при заданном состоянии xi. Проще всего рекуррентное уравнение определяется с помощью следующей двухшаговой процедуры.
Шаг 1. Выразим fi(xi) как функцию fi+1(xi+1) в виде
![]()
где fn+1(xn+1)=0.
Шаг 2. Выразим xi+1 как функцию xi для гарантии того, что левая часть последнего уравнения является функцией лишь xi. По определению xi-xi+1 представляет собой вес, загруженный на этапе і, т.е. xi-xi+1=wimi или xi+1=xi-wimi. Следовательно, рекуррентное уравнение приобретает следующий вид:
![]()
2. Практическая часть. Задача
Депутат некоторого округа баллотируется на следующий срок. Денежные средства на предвыборную кампанию составляют примерно 100000 руб. Хотя комитет по переизбранию хотел бы провести кампанию во всех пяти избирательных участках округа, ограниченность денежных средств, предписывает по-другому. Приведенная ниже таблица содержит данные о числе избирателей и денежных средств, необходимых для проведения успешной кампании по каждому избирательному участку. Каждый участок может либо использовать все предназначенные деньги, либо вовсе их не использовать. Как следует распределить денежные средства?
| Участок | Число избирателей, w | Необходимые средства (руб.), m |
| 1 | 3100 | 35000 |
| 2 | 2600 | 25000 |
| 3 | 3500 | 40000 |
| 4 | 2800 | 30000 |
| 5 | 2400 | 20000 |
По условию задачи максимальная сумма денежных средств на предвыборную кампанию не должна превышать 100000 руб., т.е. M = 100000 руб. Тогда m – необходимые средства по каждому участку, а w – число избирателей.
Построение экономико-математической модели:
число шагов N в данной задаче следует принять равным количеству избирательных участков T, т.е. 5;
фазовой переменной x является суммарная масса денежных средств на предвыборную кампанию после каждого шага управления. Ограничение: xi ≤ M;
управляющая переменная r может быть равна либо 0 (т.е. участок вовсе не использует предназначенные денежные средства), либо 1 (участок использует все предназначенные деньги);
функция процесса xi=fi(xi-1,ri), определяющая закон изменения состояния системы, для данной задачи представляется формулой xi = xi-1 + ri∙mi. Она имеет следующий смысл: суммарная масса денежных средств на предвыборную кампанию xi после шага с номером i равна суммарной массе денежных средств на предвыборную кампанию на предшествующем шаге xi-1 плюс сумма денежных средств на текущем шаге, равная ri∙mi;
частный экономический эффект представлен формулой zi=ri∙wi, а целевая функция Z=z1+z2+z3+z4+z5.
Отметим, что в данной задаче выполняются основные допущения метода динамического программирования: отсутствие последействия и аддитивность результирующей целевой функции. Значит, можно непосредственно приступить к расчетам в соответствии с методом динамического программирования.
В данном курсовом проекте все получаемые при решении задачи таблицы приведены сразу окончательно заполненными.
Предварительный этап. Данный этап проводится в естественном порядке для i=1,2,3,4,5, причем заполняются только первая строка вспомогательной таблицы и четыре левых столбца основной таблицы. Заполнение второй строки вспомогательной таблицы и оставшихся столбцов основной таблицы производится на этапе условной оптимизации. B0(x0) выражает максимальное значение сумм частных целевых функций на шагах от 1 до 5. Эта функция вычисляется с учетом функции B1(x1), которая является максимальным значением сумм частных целевых функций на шагах от 2 до 5 и т.д.
i = 1.
Вспомогательная таблица соответствует начальному условию x0=0 и имеет вид: Вспомогательная таблица на шаге 1
| x0 | 0 |
| B0(x0) | 9200 |
Заполнение основной таблицы проводится обычным образом. Для заданного единственного допустимого значения x0=0 выбираются все возможные значения управления r1 и заносятся во второй столбец таблицы. При этом r1 может принимать только значения 1 или 0. По формулам, приведенным выше, проводится расчет соответствующих значений переменных x1 и z1. Они заносятся в третий и четвертый столбцы. Получается основная таблица.
Таблица 2
Основная таблица на шаге 1
| x0 | r1 | x1 | z1 | B1(x1) | z1+B1 | B0(x0) |
| 0 | 0 1 | 0 35000 | 0 3100 | 8900 6100 | 8900 9200 | 9200 |
i = 2.
На втором шаге в первую строку вспомогательной таблицы внесем все переменные x1, рассчитанные на предшествующем шаге и фигурирующие в третьем столбце предыдущей основной таблицы:
Таблица 3
Вспомогательная таблица на шаге 2
| x1 | 0 | 35000 |
| B1(x1) | 8900 | 6100 |
Для заполнения основной таблицы будем последовательно выбирать все допустимые значения х1, внесенные во вспомогательную таблицу, и проводить соответствующие расчеты:
Таблица 4
Основная таблица на шаге 2
| x1 | r2 | x2 | z2 | B2(x2) | z2+B2 | B1(x1) |
| 0 | 0 1 | 0 25000 | 0 2600 | 8700 6300 | 8700 8900 | 8900 |
| 35000 | 0 1 | 35000 60000 | 0 2600 | 5900 3500 | 5900 6100 | 6100 |
Аналогичные расчеты производятся на остальных этапах решения.
i = 3.
Таблица 5
Вспомогательная таблица на шаге 3
| x2 | 0 | 25000 | 35000 | 60000 |
| B2(x2) | 8700 | 6300 | 5900 | 3500 |
Таблица 6
Основная таблица на шаге 3
| x2 | r3 | x3 | z3 | B3(x3) | z3+B3 | B2(x2) |
| 0 | 0 1 | 0 40000 | 0 3500 | 5200 5200 | 5200 8700 | 8700 |
| 25000 | 0 1 | 25000 65000 | 0 35000 | 5200 2800 | 5200 6300 | 6300 |
| 35000 | 0 1 | 35000 75000 | 0 3500 | 5200 2400 | 5200 5900 | 5900 |
| 60000 | 0 1 | 60000 100000 | 0 3500 | 2800 0 | 2800 3500 | 3500 |
i = 4.
Таблица 7
Вспомогательная таблица на шаге 4
| x3 | 0 | 25000 | 35000 | 40000 | 60000 | 65000 | 75000 | 100000 |
| B3(x3) | 5200 | 5200 | 5200 | 5200 | 2800 | 2800 | 2400 | 0 |
Таблица 8
Основная таблица на шаге 4
| x3 | r4 | x4 | z4 | B4(x4) | z4+B4 | B3(x3) |
| 0 | 0 1 | 0 30000 | 0 2800 | 2400 2400 | 2400 5200 | 5200 |
| 25000 | 0 1 | 25000 55000 | 0 2800 | 2400 2400 | 2400 5200 | 5200 |
| 35000 | 0 1 | 35000 65000 | 0 2800 | 2400 2400 | 2400 5200 | 5200 |
| 40000 | 0 1 | 40000 70000 | 0 2800 | 2400 2400 | 2400 5200 | 5200 |
| 60000 | 0 1 | 60000 90000 | 0 2800 | 2400 0 | 2400 2800 | 2800 |
| 65000 | 0 1 | 65000 95000 | 0 2800 | 2400 0 | 2400 2800 | 2800 |
| 75000 | 0 | 75000 | 0 | 2400 | 2400 | 2400 |
| 100000 | 0 | 100000 | 0 | 0 | 0 | 0 |
i = 5.
Таблица 9
Вспомогательная таблица на шаге 5
| x3 | 0 | 25000 | 30000 | 35000 | 40000 | 55000 | 60000 | 65000 |
| B3(x3) | 2400 | 2400 | 2400 | 2400 | 2400 | 2400 | 2400 | 2400 |
| x3 | 70000 | 75000 | 90000 | 95000 | 100000 | |||
| B3(x3) | 2400 | 2400 | 0 | 0 | 0 | |||
Таблица 10
Основная таблица на шаге 5
| x4 | r5 | x5 | z5 | B5(x5) | z5+B5 | B4(x4) |
| 0 | 0 1 | 0 20000 | 0 2400 | 0 0 | 0 2400 | 2400 |
| 25000 | 0 1 | 25000 45000 | 0 2400 | 0 0 | 0 2400 | 2400 |
| 30000 | 0 1 | 30000 50000 | 0 2400 | 0 0 | 0 2400 | 2400 |
| 35000 | 0 1 | 35000 55000 | 0 2400 | 0 0 | 0 2400 | 2400 |
| 40000 | 0 1 | 40000 60000 | 0 2400 | 0 0 | 0 2400 | 2400 |
| 55000 | 0 1 | 55000 75000 | 0 2400 | 0 0 | 0 2400 | 2400 |
| 60000 | 0 1 | 60000 80000 | 0 2400 | 0 0 | 0 2400 | 2400 |
| 65000 | 0 1 | 65000 85000 | 0 2400 | 0 0 | 0 2400 | 2400 |
| 70000 | 0 1 | 70000 90000 | 0 2400 | 0 0 | 0 2400 | 2400 |
| 75000 | 0 1 | 75000 95000 | 0 2400 | 0 0 | 0 2400 | 2400 |
| 90000 | 0 | 90000 | 0 | 0 | 0 | 0 |
| 95000 | 0 | 95000 | 0 | 0 | 0 | 0 |
| 100000 | 0 | 100000 | 0 | 0 | 0 | 0 |
На этом предварительный этап завершен. Далее проводится этап условной оптимизации.
Этап условной оптимизации. Данный этап непосредственно связан с вычислением функций Bi(xi) и проводится в обратном порядке для i=5,4,3,2,1. Поскольку в соответствии с общим принципом оптимальности Беллмана имеет место равенство В5(х5)=0, т.к. на последнем шаге управления дальнейших изменений системы не происходит и соответствующий экономический эффект равен 0, то в пятый столбец основной таблицы, полученной при i=5, записываем нулевые значения. При этом в шестой столбец записываются суммы соответствующих чисел из двух предшествующих столбцов, а в последний столбец заносится максимум из всех чисел шестого столбца для каждого строчного фрагмента отдельно. Полученные значения функции В4(х4) заносятся во вторую строку вспомогательной таблицы. Заполненные таблицы уже приведены выше. Аналогично завершается заполнение основных и вспомогательных таблиц для i=4,3,2,1.
Этап безусловной оптимизации. На данном этапе определяются оптимальное значение задачи Z* и оптимальное управление (r1*,r2*,r3*). Поскольку начальное состояние x0 =0 задано однозначно, то Z*=B0(x0)= 9200 избирателей, x0*=x0=0. Для построения оптимального управления просмотрим все заполненные основные таблицы в естественном порядке при i=1,2,3,4.5 используя отмеченные знаками « » строки, содержащие условно-оптимальные значения управления. Получаем такую последовательность шагов: i = 1: x0* = 0, r1* = 1, x1* = 35000.
i = 2: x1* = 35000, r2* = 1, x2* = 60000.
i = 3: x2* = 60000, r3* = 1, x3* = 100000.
i = 4: x3* = 100000, r4* = 0, x4* = 100000.
i = 5: x4* = 100000, r5* = 0, x5* = 100000.
Следовательно, оптимальное решение данной задачи имеет вид (1,1,1,0,0).
По итогам решения данной задачи можно сделать следующие выводы:
максимальное число избирателей при оптимальном распределении ресурсов составит 9200 человек;
в задаче существует только одно оптимальное решение (1,1,1,0,0), которое означает, что комитет по переизбранию должен провести предвыборную кампанию только в первых трех избирательных участках;
сумма используемых денежных средств в случае оптимального их распределения составит ровно 100000 руб.
Список использованной литературы.
Беллман Р., Дрейфус С. Прикладные задачи динамического программирования. – М.:Наука,1965.-458 с.
Вентцель Е. С. Элементы динамического программирования. –М.: Наука,1987. – 218 c.
Вилкас Э.И. Оптимальность в играх и решениях. - М.: Наука,1990.-256с
Давыдов, Э.Г. Исследование операций : учеб. пособие для студ. вузов / Э.Г. Давыдов. - М. : Высш. школа, 1990. – 383 с.
Заварыкин В.М., Житомирский В.Г., Лапчик М.П. Численные методы. – М.: Просвещение, 1991 г.-176 с.
Информатика. Учебник. /Под ред. И.В.Макаровой. – 3-е изд.перераб. М.:Финансы и статистика, 2005-768 с.
Карманов В. Т. Математическое программирование. –М.:Наука,1986. – 312 с.

| Автор | |
|---|---|
| Дата добавления | 14.12.2018 |
| Раздел | Высшая математика |
| Подраздел | Научная работа |
| Просмотров | 1982 |
| Номер материала | 5984 |