
Презентация " Параллельность и перпендикулярность" (наглядная геометрия, 6 кл.)


















Описание презентации по отдельным слайдам:
Параллельные и перпендикулярные прямые играют очень большую роль в жизни человека: особенности их взаимного расположения используют в строительстве, технике, искусстве. Теория параллельных занимает одно из центральных мест в науке «геометрия». Именно свойства параллельных прямых определяют основные свойства изучаемого нами пространства.
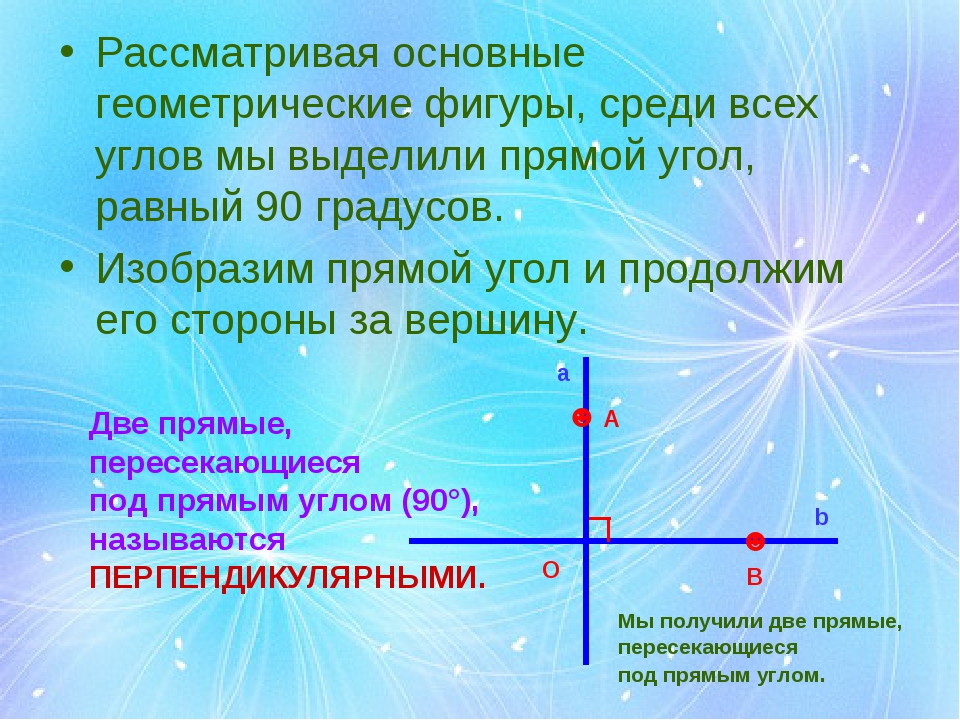
Рассматривая основные геометрические фигуры, среди всех углов мы выделили прямой угол, равный 90 градусов. Изобразим прямой угол и продолжим его стороны за вершину. ☻ ☻ O В А a b Мы получили две прямые, пересекающиеся под прямым углом. Две прямые, пересекающиеся под прямым углом (90°), называются ПЕРПЕНДИКУЛЯРНЫМИ.
Перпендикулярные прямые обладают интересными свойствами. 1. Через точку вне данной прямой можно провести только одну прямую, перпендикулярную этой прямой и пересекающую ее. 2. Если точку взять на самой прямой, то через эту точку проходит бесконечное число прямых, перпендикулярных данной прямой.
Если начертить прямую в тетради, то одна из прямых, перпендикулярных ей, будет лежать в плоскости тетради, а все остальные прокалывать тетрадь в данной точке. Они будут находиться в пространстве (вне плоскости листа); это похоже на дорожный столб, стоящий на перекрестке дорог: столб перпендикулярен каждой дороге (рис. 2). Рис. 2 Рис. 3 3. Две прямые на плоскости, перпендикулярные третьей прямой, не могут пересечься одна с другой (рис. 3). Если бы они пересеклись, например, в точке С, то мы получили бы треугольник ABC, у которого два прямых угла, что невозможно. На плоскости такого не может быть.
А вот на сфере перпендикуляры ведут себя иначе. Вспомните экватор и меридианы. Они перпендикулярны друг к другу, но все меридианы пересекаются в одной точке — на ПОЛЮСЕ. Однако вернемся к плоскости. Итак, свойство 3 говорит о том, что на плоскости существуют непересекающиеся прямые. Две прямые на плоскости называются ПАРАЛЛЕЛЬНЫМИ, если они не пересекаются. a b
Передвигая, как показано на рисунке, треугольник вдоль неподвижной линейки, получаем множество параллельных между собой прямых. На рисунке 4-в прямые m и n параллельны. Этот факт записывается так: m║n Читаем: прямая m параллельна прямой n Выбор именно такого знака достаточно понятен, не так ли? Рис. 4 а б Используя линейку и чертежный угольник, можно без труда вычерчивать параллельные прямые
У обычного чертежного угольника один угол прямой. В этом случае с его помощью можно проводить прямые, перпендикулярные данной прямой (рис. 5). Или, как говорят, опускать на данную прямую перпендикуляры или восставлять к ней перпендикуляры. То, что прямые m и n перпендикулярны, записывается так: m n. С помощью циркуля и линейки также можно строить параллельные и перпендикулярные прямые. Предлагаемые ниже способы построения интересны и тем, что число проводимых при построении линий будет наименьшим из возможных. Рис. 5
Проведение параллельных прямых Пусть проведена прямая ℓ и дана точка А вне этой прямой (рис. 6). Проведем через точку А любую окружность, пересекающую прямую ℓ (рис. 6). Возьмем одну из точек пересечения окружности с прямой — точку В, измерим циркулем отрезок АВ и проведем окружность радиусом, равным АВ, с центром в точке В1. Появится точка А1. Прямая, проходящая через точки А и А1, параллельна прямой ℓ. Рис. 6
Проведение перпендикуляра к прямой Пусть проведена прямая ℓ и дана точка А вне этой прямой. Для построения перпендикуляра достаточно с помощью циркуля провести через А две произвольные окружности с центрами на прямой ℓ (рис.7). Вторая точка пересечения этих окружностей (точка А1) и даст нам вторую точку на перпендикуляре. Подумайте, как провести перпендикуляр (с помощью циркуля и линейки), если точка А лежит на прямой ℓ… Поэтапное построение
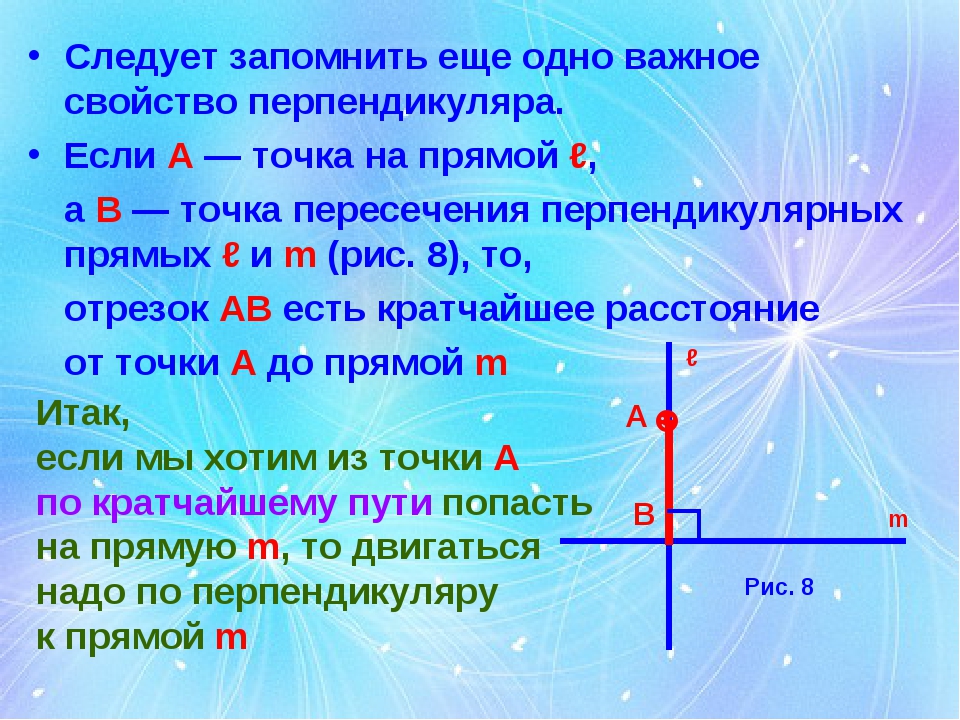
Следует запомнить еще одно важное свойство перпендикуляра. Если А — точка на прямой ℓ, а В — точка пересечения перпендикулярных прямых ℓ и m (рис. 8), то, отрезок АВ есть кратчайшее расстояние от точки А до прямой m ℓ m ☻ A B Рис. 8 Итак, если мы хотим из точки А по кратчайшему пути попасть на прямую m, то двигаться надо по перпендикуляру к прямой m
Мы все время говорили: «параллельные прямые», «перпендикулярные прямые». Понятно, что на практике мы имеем дело не с прямыми, а лишь с их частями — отрезками, лежащими на этих прямых. Отрезки, лежащие на параллельных прямых, также называются ПАРАЛЛЕЛЬНЫМИ, а на перпендикулярных - ПЕРПЕНДИКУЛЯРНЫМИ.
Среди ребер куба можно указать пары параллельных и перпендикулярных ребер. На рисунке 9 изображен куб. Рис. 9 С Три четверки его ребер параллельны между собой. Вот одна из них: АВ || DC || АХВХ || DXCX. 1. Назовите еще две четверки параллельных между собой ребер куба. Ребро АА1 перпендикулярно ребрам АВ, А1В1, AD и A1D1. Угол между ребром АА1 и каждым из этих ребер равен 90°. 2. Назовите ребра, перпендикулярные: а) ребру СС1; б) ребру DC.
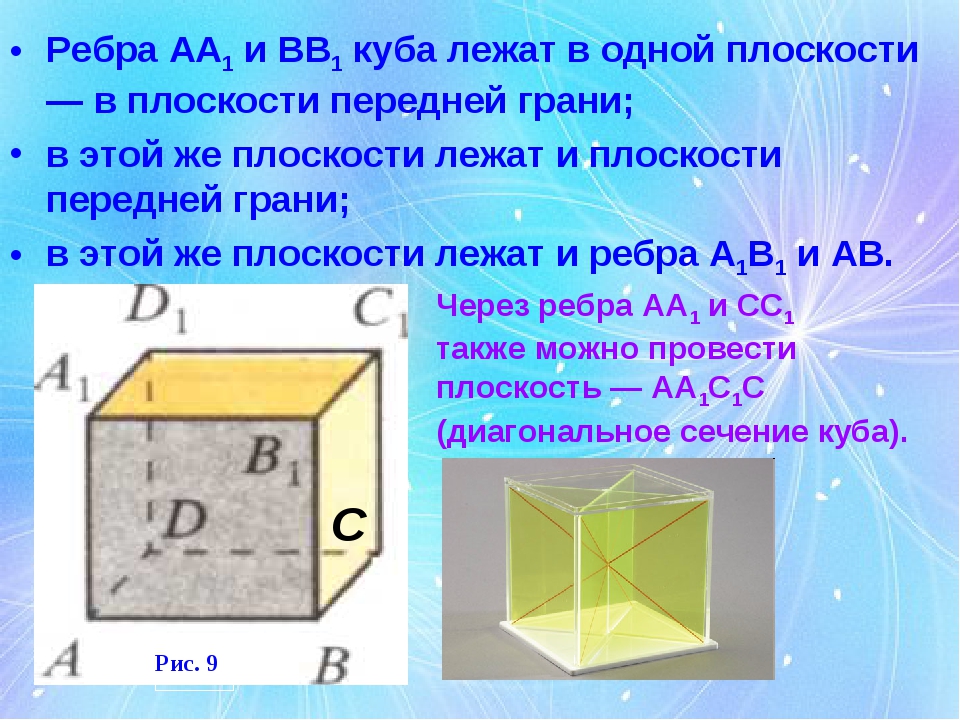
Ребра АА1 и ВВ1 куба лежат в одной плоскости — в плоскости передней грани; в этой же плоскости лежат и плоскости передней грани; в этой же плоскости лежат и ребра А1В1 и АВ. Рис. 9 С Через ребра АА1 и СС1 также можно провести плоскость — АА1С1С (диагональное сечение куба).
А вот пара ребер АА1 и D1C1 особенная. Не существует плоскости, которая бы проходила через оба эти отрезка (а также через прямые АА1 и D1C1). Такие отрезки и прямые называются СКРЕЩИВАЮЩИМИСЯ. Какую бы плоскость мы ни провели через АА1, обязательно прямая D1C1 либо пересечет ее в какой-либо одной точке, либо не пересечет никогда. 3. Найдите еще несколько пар скрещивающихся ребер куба AC1. С Обозначение: a b ☻ Читают: прямые a и b - скрещивающиеся
За 5 мин привести как можно больше примеров: 1) параллельных прямых 2) перпендикулярных прямых, встречающихся в окружающем нас мире. Участники поочередно называют примеры таких прямых. Игра заканчивается, как только в течение минуты никто не может придумать новый пример. Побеждает тот, чей пример был последним.
Найдите на рисунке 9 какие-либо отрезки с концами в вершинах куба (не являющиеся его ребрами), такие, чтобы они были: а) параллельными; б) перпендикулярными; в) скрещивающимися. С
Домашнее задание Выполнить все построения, которые выполняли на уроке, выделяя цветом главные этапы и линии, на альбомном листе А-4.

| Автор | |
|---|---|
| Дата добавления | 27.12.2018 |
| Раздел | Математика |
| Подраздел | Презентация |
| Просмотров | 5034 |
| Номер материала | 6019 |