Презентация по математике Соколовой Е. (11 "Б" класс) на тему "Призма"

























Описание презентации по отдельным слайдам:
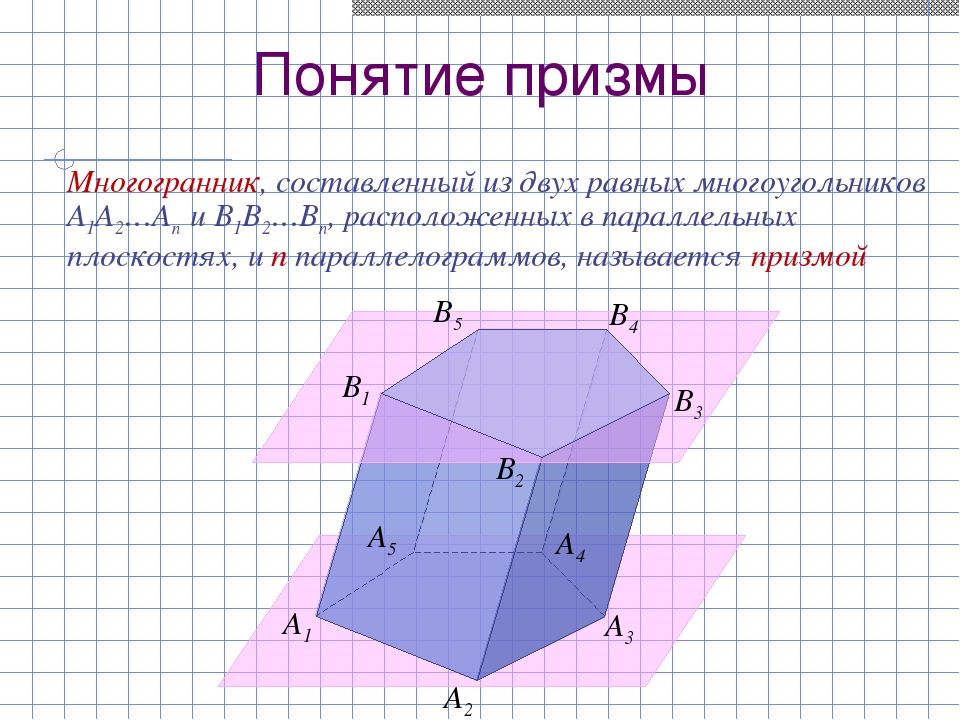
Понятие призмы Многогранник, составленный из двух равных многоугольников A1A2…An и B1B2…Bn, расположенных в параллельных плоскостях, и n параллелограммов, называется призмой A1 A2 A3 A4 A5 В1 В2 В3 В4 В5
Многоугольники A1A2…An и B1B2…Bn называются основаниями призмы а параллелограммы – боковыми гранями призмы A1 A2 A3 A4 A5 В1 В2 В3 В4 В5 A1 A2 A3 A4 A5 В1 В2 В3 В4 В5
Отрезки A1B1, A2B2, … , AnBn называются боковыми ребрами призмы Боковые ребра призмы равны и параллельны A1 A2 A3 A4 A5 В1 В2 В3 В4 В5 A1 A2 A3 A4 A5 В1 В2 В3 В4 В5 Вершины многоугольников A1, A2, …, An и B1, B2, …, Bn называются вершинами призмы
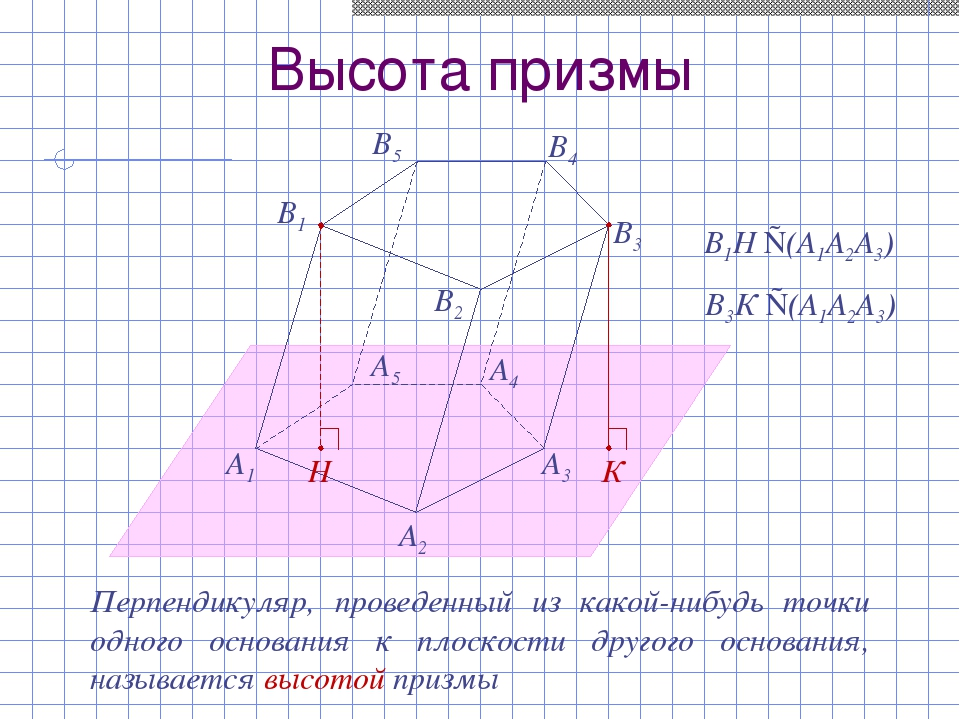
Высота призмы A1 A2 A3 A4 A5 В1 В2 В3 В4 В5 К Н Перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого основания, называется высотой призмы В1Н ⊥(А1А2А3) В3К ⊥(А1А2А3)
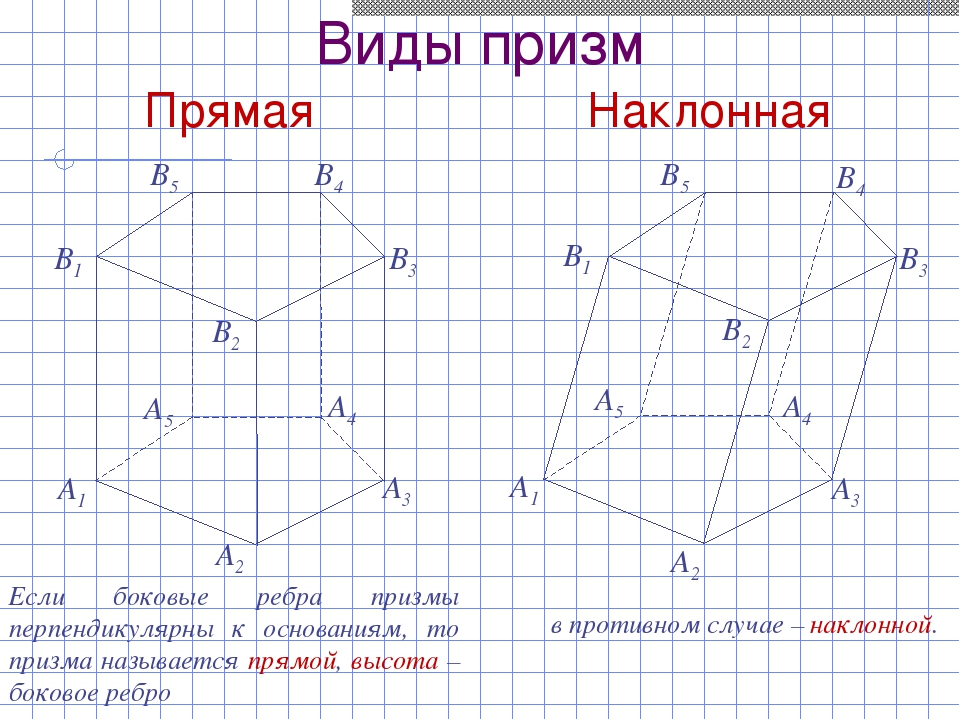
Виды призм A1 A2 A3 A4 A5 В1 В2 В3 В4 В5 Если боковые ребра призмы перпендикулярны к основаниям, то призма называется прямой, высота – боковое ребро A1 A2 A3 A4 A5 В1 В2 В3 В4 В5 в противном случае – наклонной. Прямая Наклонная
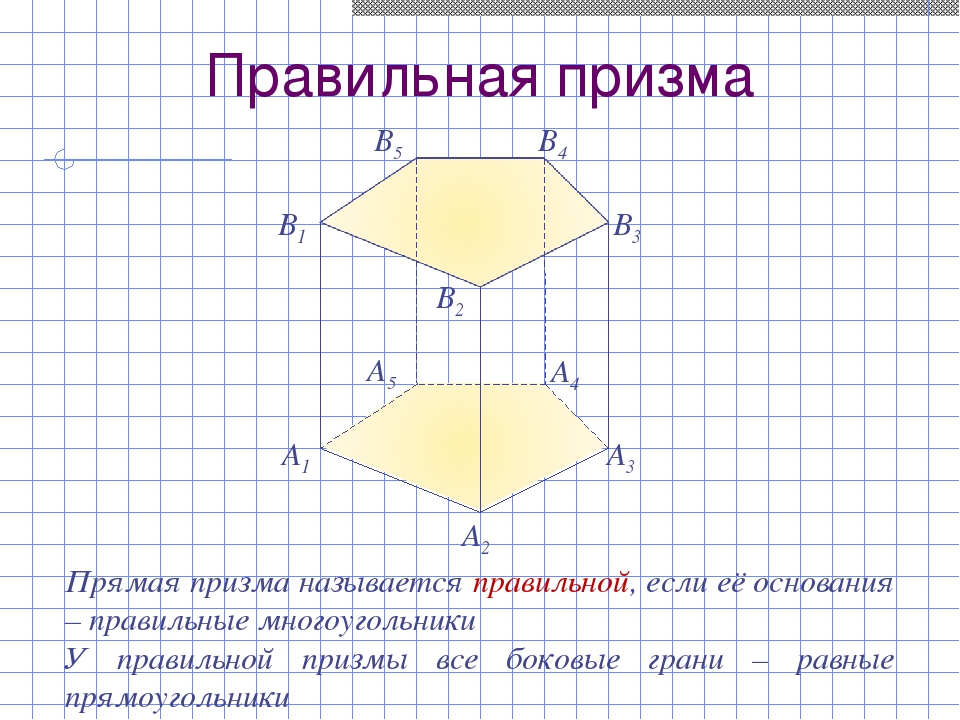
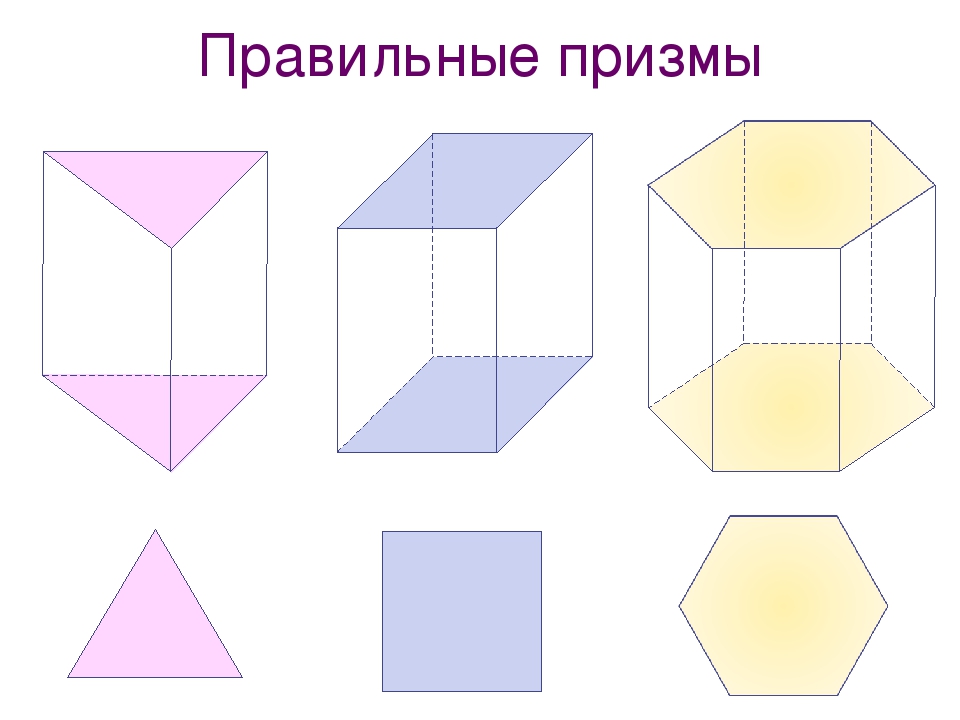
Правильная призма A1 A2 A3 A4 A5 В1 В2 В3 В4 В5 Прямая призма называется правильной, если её основания – правильные многоугольники У правильной призмы все боковые грани – равные прямоугольники
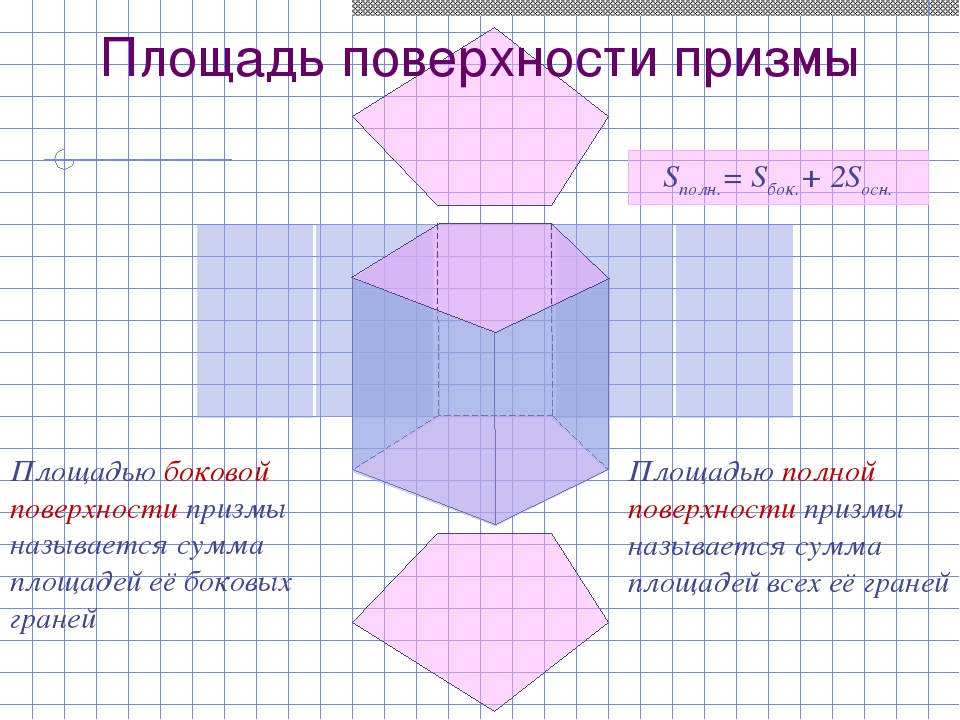
Площадью боковой поверхности призмы называется сумма площадей её боковых граней Площадью полной поверхности призмы называется сумма площадей всех её граней Площадь поверхности призмы Sполн.= Sбок.+ 2Sосн.
Теорема о площади боковой поверхности прямой призмы Площадь боковой поверхности прямой призмы равна произведению периметра основания на высоту призмы Доказательство. Боковые грани прямой призмы – прямоугольники, основания которых – стороны основания призмы, а высоты равны высоте h призмы. Sбок. = A1A2· h + A2A3· h + A3A4· h + … + An-1An· h = = (A1A2 + A2A3 + A3A4 + … + An-1An) · h = Pосн.· h Sбок. = Росн.· h
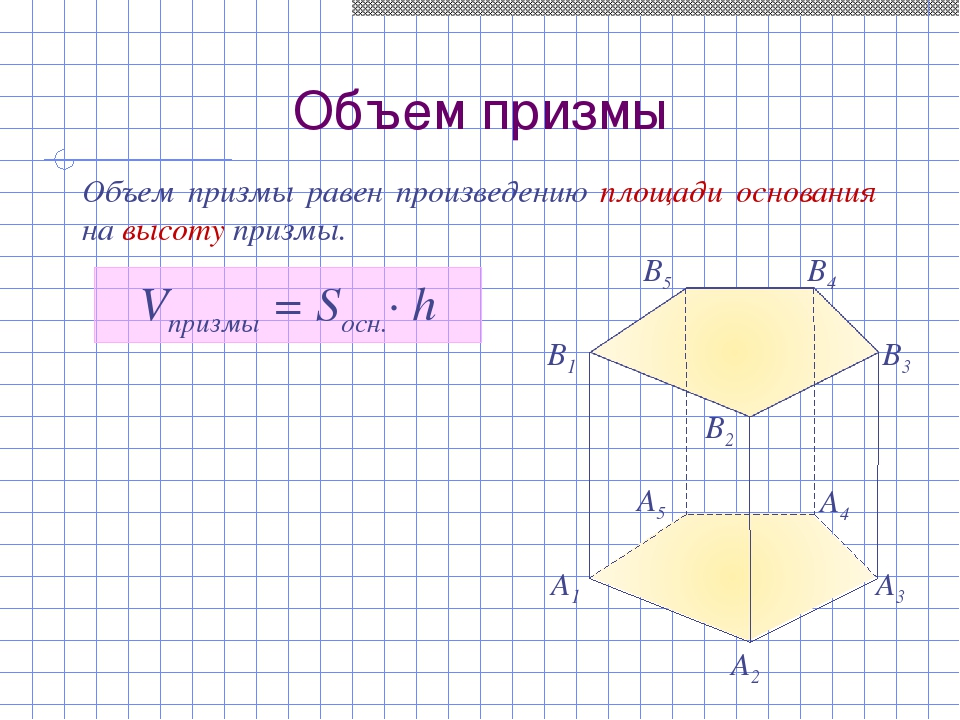
Объем призмы Объем призмы равен произведению площади основания на высоту призмы. Vпризмы = Sосн.· h
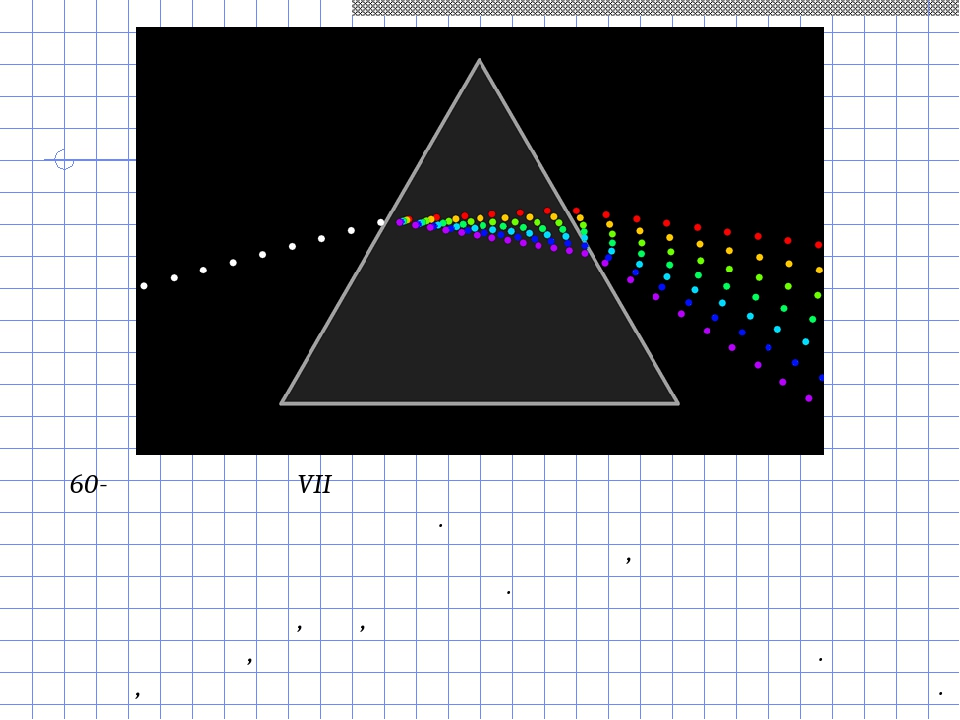
В 60-х годах ХVII столетия Исаак Ньютон проводил эксперименты со светом. Чтобы разложить свет на составляющие и получить спектр, он использовал трехгранную стеклянную призму. Ученый обнаружил, что, собрав раздробленный луч с помощью второй призмы, можно опять получить белый свет. Так он доказал, что белый свет является смесью разных цветов. Проходя через призму, световые лучи преломляются.
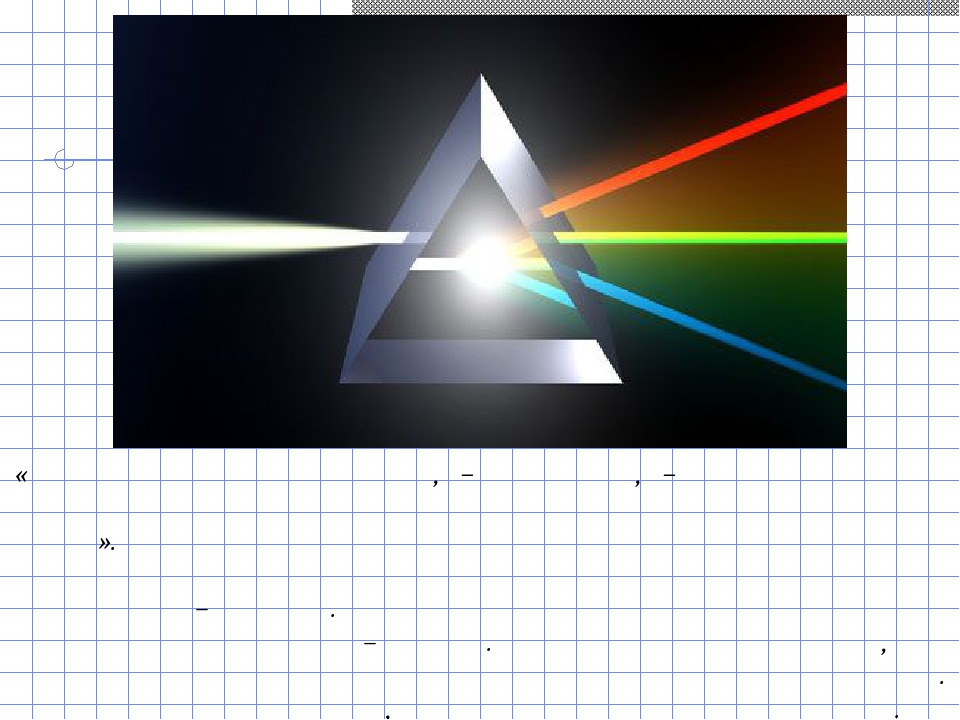
«Я затемнил мою комнату, − писал он, − и сделал очень маленькое отверстие в ставне для пропуска солнечного света». На пути солнечного луча ученый поставил особое трехгранное стеклышко – призму. На противоположной стене он увидел разноцветную полоску – спектр. Ньютон объяснил это тем, что призма разложила белый цвет на составляющие его цвета. Ньютон первый разгадал, что солнечный луч многоцветный.
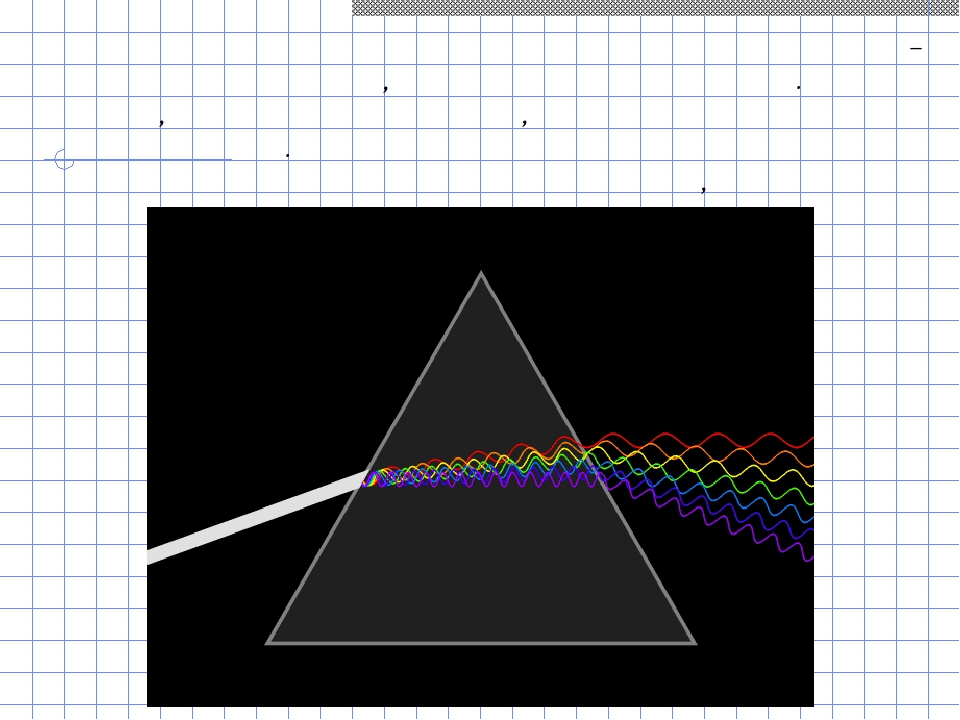
Но лучи разного цвета преломляются в разной степени – красный в наименьшей, фиолетовый в наибольшей. Именно поэтому, проходя через призму, белый цвет дробится на составные цвета. Преломление света называется рефракцией, а разложение белого света на разные цвета – дисперсией.
Архитектура, оптика, медицина, электронная техника. (очки, бинокли, объективы, телефоны)
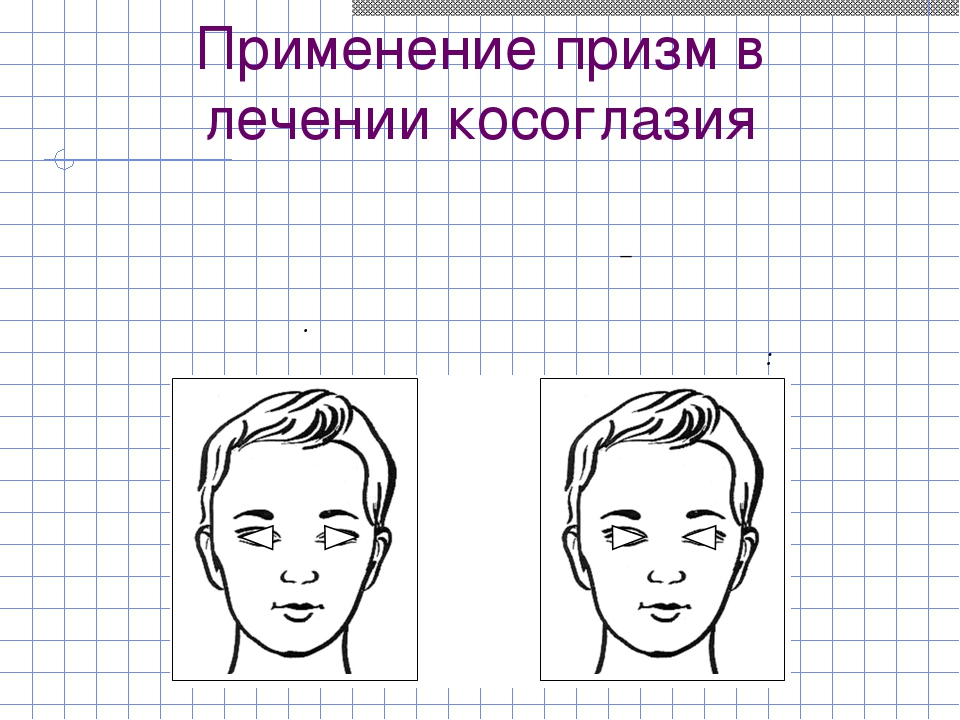
Применение призм в лечении косоглазия Принцип тренировки состоит в попеременном приставлении к тренируемым глазам на определенное время положительных сферо – призматических элементов различной сферической и призматической диоптрийности. Графически это выглядит следующим образом:

| Автор | |
|---|---|
| Дата добавления | 03.06.2019 |
| Раздел | Геометрия |
| Подраздел | Презентация |
| Просмотров | 2263 |
| Номер материала | 6262 |