
Презентация "Подмножество"

Краткое описание документа:
В презентационном уроке под названием «Подмножество» разбирается школьниками 7-го класса понятие «подмножество». Для учащихся, в первую очередь, стоит дать понять, что суть подмножества состоит в том, что оно является неотъемлемой частью множества.


слайды 1-2 (Тема презентации "Подмножество ", пример)
После титульного листа презентации сразу идут наглядный пример того, что множество В являетсяподмножеством множества А. В данном случае школьники должны уяснить, что множество В является частьюмножества А из-за того, что элементы множества В являются одновременно частью группы элементовмножества А.


слайды 3-4 (примеры. определение подмножества)
На следующем слайде данное объяснение дано в виде расшифровки понятия «подмножество». Учитываято, что каждый элемент множества В является элементом множества А, эти оба множества следуетсоответственно обозначить в краткой форме. Поэтому прямо под понятием указана форма обозначенияподобного явления в математике.
Далее для лучшего закрепления полученного материала учащиеся должны разобраться в примерах,связанных с данной темой. Первый пример включает себя образец подмножества натуральных чисел. Затемв качестве второго примера выступает подмножество из четных чисел, кратных 4-ем. Заключительныйпример говорит о том, что множество точек на определенном отрезке также может являться подмножествомдля множества точек другого отрезка, гораздо большего по размерам, в котором содержится первыйотрезок.
слайды 5-6 (круги Эйлера, примеры)
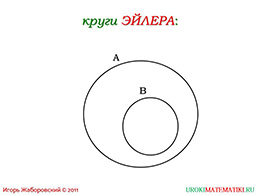
Уходя от этих примеров, учитель должен дальше объяснить что значат для математики круги Эйлера. Впрезентации их изображение имеется, поэтому ученикам нужно разъяснить, что эти круги, являютсяспециальной геометрической схемой, с помощью которой можно легко представить себе отношения междумножеством и его подмножеством. Такой метод помогает логически применить полученные знания в решенииопределенных задач. Также круги Эйлера способны значительно легче приходить к нужным рассуждениям.Применяя подобный метод в учебной программе, можно не только улучшить восприятие учеников, но иразвить у них логическое мышление, так как круги Эйлера относятся больше к логической науке, нежели ксамой математике.
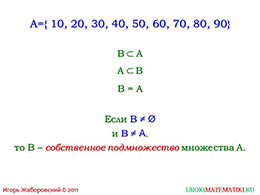
В следующем слайде презентации «Подмножество» дан пример о том, что два множества могут быть равныдруг с другом, и содержатся друг в друге соответственно. Ниже представлен особый случай, при котороммножество В, не являясь пустым множеством, а также равным со множеством А, содержится во множестве А.Такое явление называется не иначе, как собственное подмножество заданного множества.

слайд 7 (пример)
Последним этапом в изучении этой темы является то, что пустое подмножество должно обязательно являться подмножеством какого-либо множества, в то время как любое множество может считаться собственным подмножеством.
После того, как по последней части презентации «Подмножество» будут выполнены необходимые упражнения для общего закрепления материала, учителю могут быть заданы вопросы, возникшие в течение урока по соответствующей тематике. Данная презентация станет прекрасным наглядным пособием, как для учителей, так и для учеников. Она подходит и для самостоятельного изучения материала, и для обучения с помощью репетитора, а также для дистанционного обучения. Простота и наглядность презентации позволяет легче разъяснить абсолютно абстрактные для детского понимания явления в сфере математики. В любом случае работа с данным пособием является более понятным, нежели обычное чтение учебника по математике. К тому же имея у себя этот наглядный материал, можно при необходимости повторить урок в любое удобное время.
| Автор | |
|---|---|
| Дата добавления | 25.07.2014 |
| Раздел | Алгебра |
| Подраздел | Презентация |
| Просмотров | 6961 |
| Номер материала | 179 |