Презентация " Трапеция" 8 класс

8 класс геометрия Учитель: Матвеенко Вера николаевна

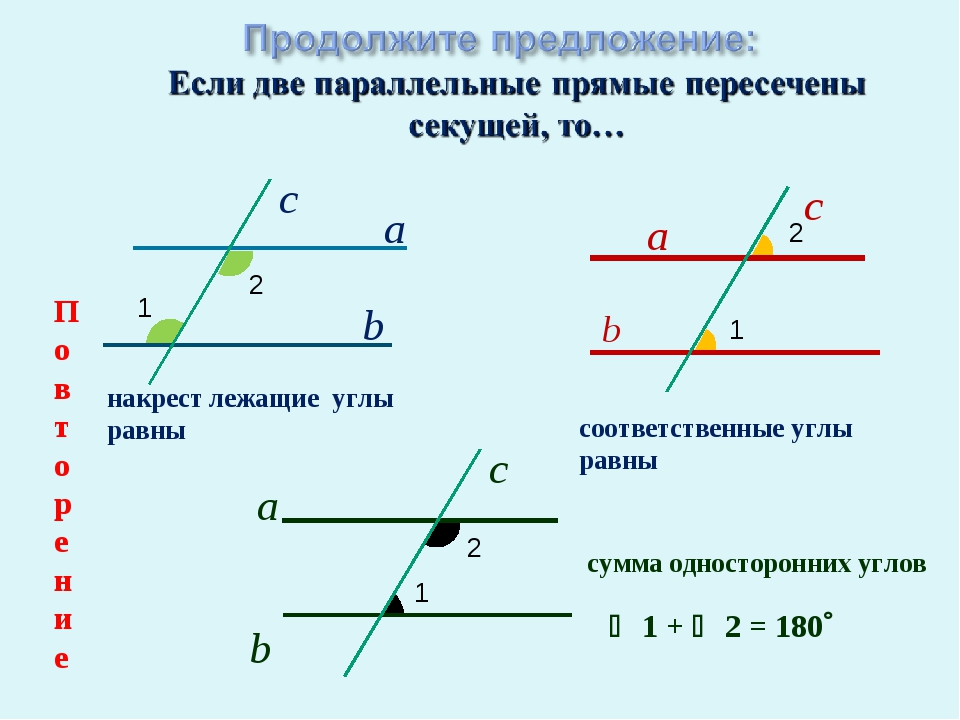
а c b а c b а c b  1 +  2 = 180 1 2 1 1 2 2 накрест лежащие углы равны соответственные углы равны сумма односторонних углов Повторение

Повторение

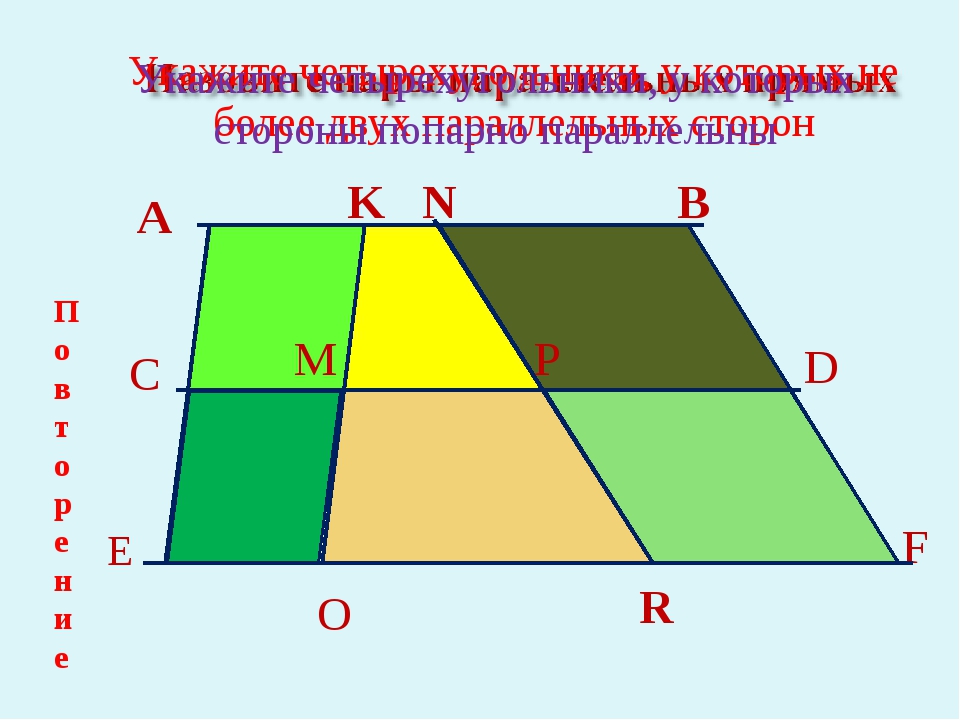
А B C D E F K M O R P N Укажите четырехугольники, у которых не более двух параллельных сторон Укажите четырехугольники, у которых стороны попарно параллельны Повторение

А B C D AB CD, AC BD Какой четырехугольник называется параллелограммом? Повторение

А В С Д Повторение

А Повторение

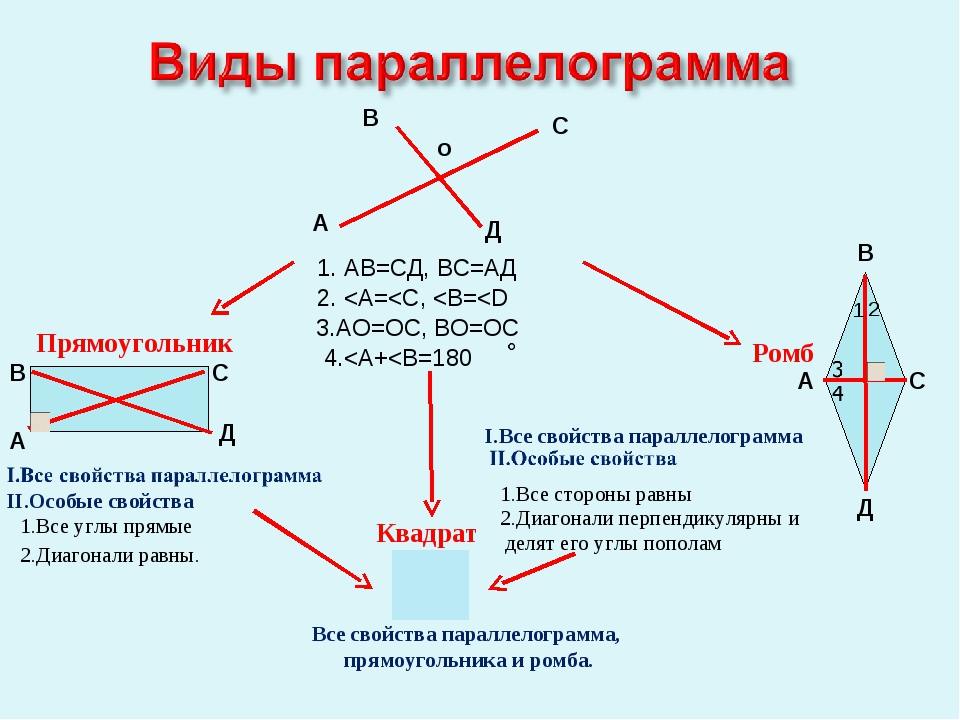
А В С Д 1. АВ=СД, ВС=АД 2. <A=<C, <B=<D o 3.AO=OC, BO=OC 4.<A+<B=180 Прямоугольник Ромб А В С Д А В С Д 1 2 I.Все свойства параллелограмма II.Особые свойства 1.Все углы прямые 2.Диагонали равны. 1.Все стороны равны 2.Диагонали перпендикулярны и делят его углы пополам Квадрат Все свойства параллелограмма, прямоугольника и ромба.

Ответьте на вопросы Из чего составлена данная геометрическая фигура? Какими должны быть треугольники, составляющие эту фигуру? Как составляются треугольники и прямоугольник? А что вы знаете о противоположных сторонах прямоугольника? Значит, и в данном четырёхугольнике будут параллельные стороны? Сколько их? Параллельны ли две другие стороны?

2 пары параллельных сторон 1 пара параллельных сторон Нет параллельных сторон параллелограмм трапеция

-это четырехугольник ,у которого 2 пары параллельных сторон четырехугольник Трапеция 1 пара параллельных сторон Параллелограмм

Что такое трапеция? Трапецией называется четырёхугольник, у которого две стороны параллельны, а две другие стороны не параллельны. верхнее основание нижнее основание боковая сторона боковая сторона 1

Слово трапеция произошло от греческого слова "столик" (от того же корня происходит и слово "трапеза"). 2

Применение формы трапеции в повседневной жизни в интерьерах (диваны, стены, навесные потолки); в ландшафтном дизайне (границы газонов, искусственных водоемов, формы камней); в индустрии моды (одежда, обувь, аксессуары); в дизайне предметов повседневного пользования (светильники, чайники, пылесосы с использованием форм трапеции и т.д.); в архитектуре 3

Интерьер 4

Ландшафтный дизайн 5

Архитектура 6

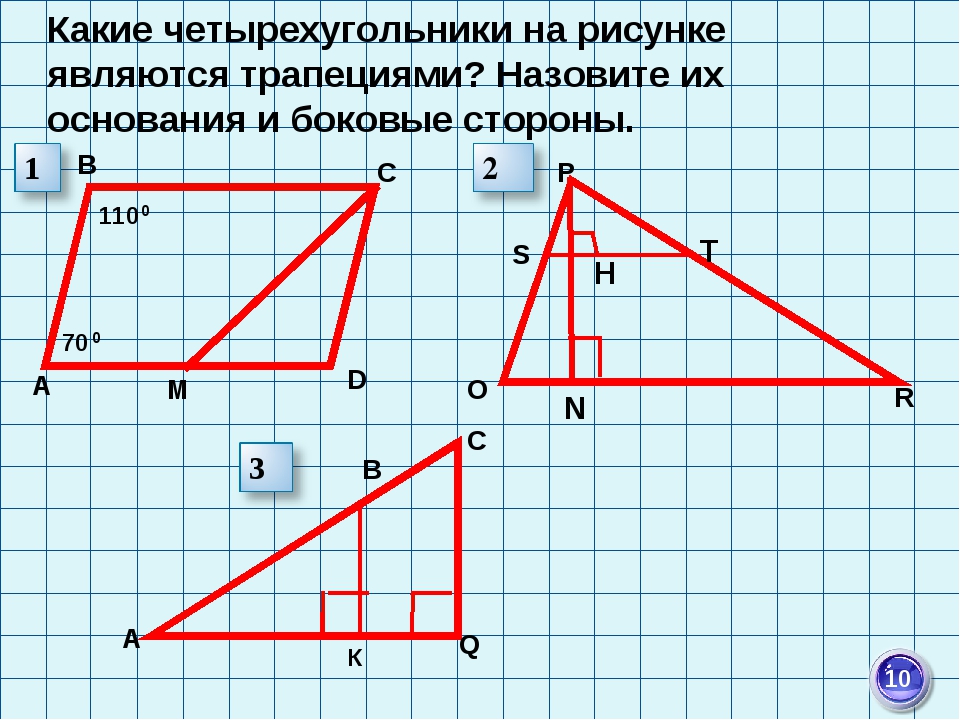
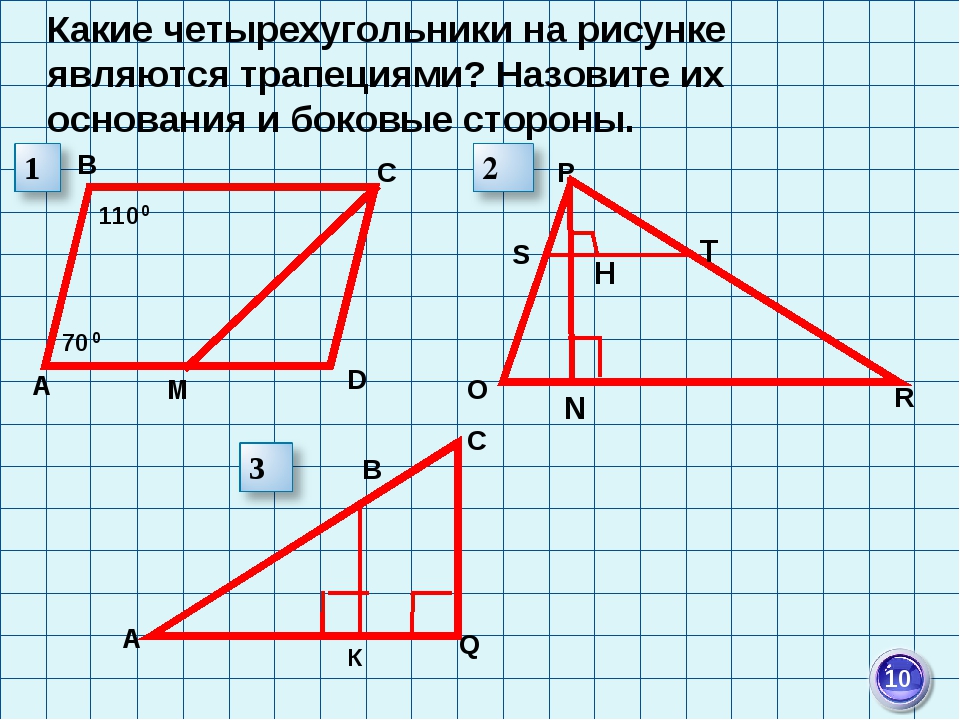
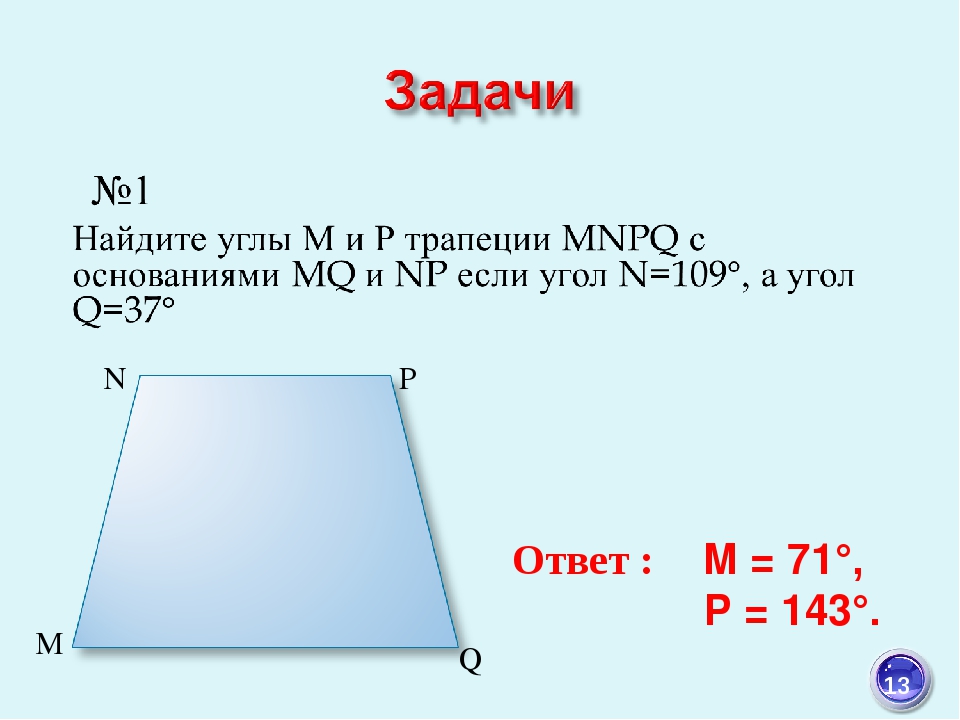
Какие четырехугольники на рисунке являются трапециями? Назовите их основания и боковые стороны. 70 110 А В С D М О Р R S H T N 0 0 А С В К Q 10

Задание №1 3 4 7

Проверь себя 3 4 8

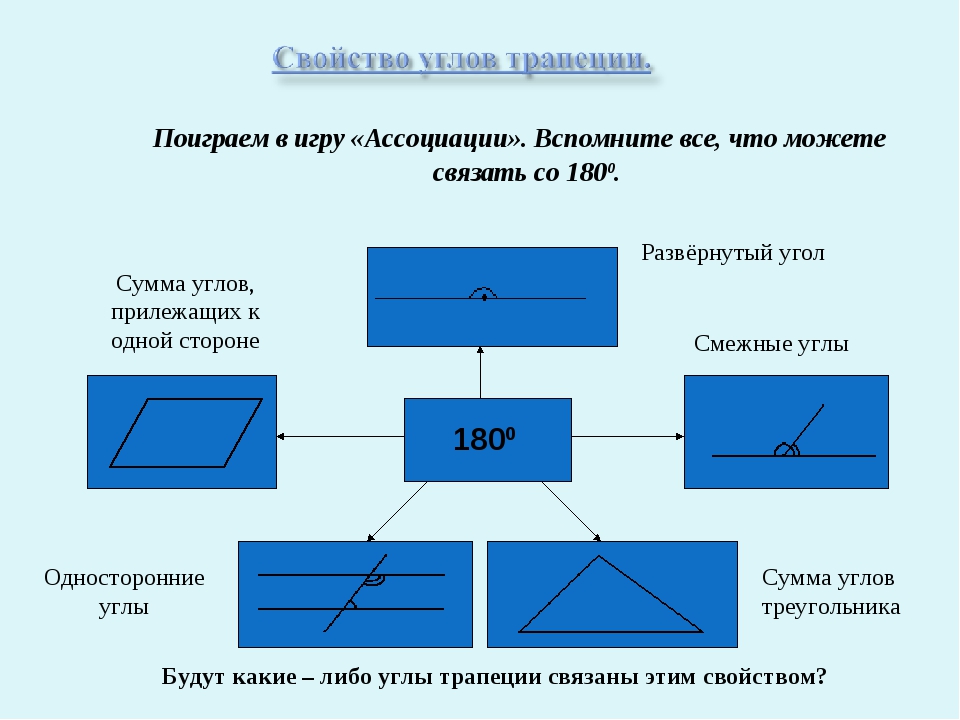
Поиграем в игру «Ассоциации». Вспомните все, что можете связать со 1800. 1800 Развёрнутый угол Смежные углы Сумма углов треугольника Односторонние углы Сумма углов, прилежащих к одной стороне Будут какие – либо углы трапеции связаны этим свойством?

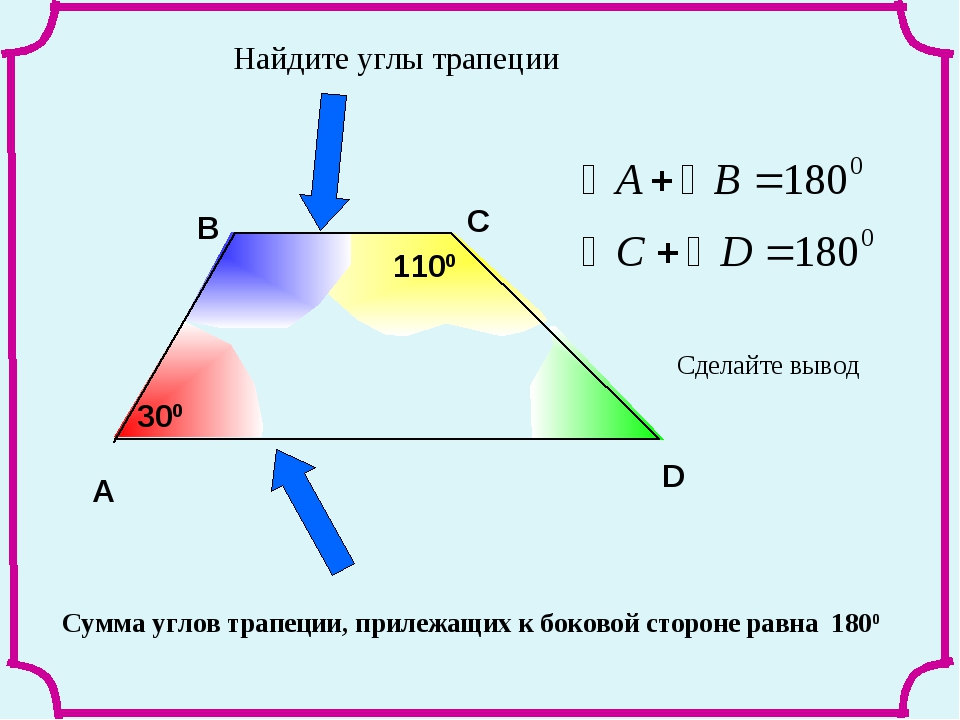
A В С D Найдите углы трапеции 300 1100 Сделайте вывод Сумма углов трапеции, прилежащих к боковой стороне равна 1800

Какие четырехугольники на рисунке являются трапециями? Назовите их основания и боковые стороны. 70 110 А В С D М О Р R S H T N 0 0 А С В К Q 10

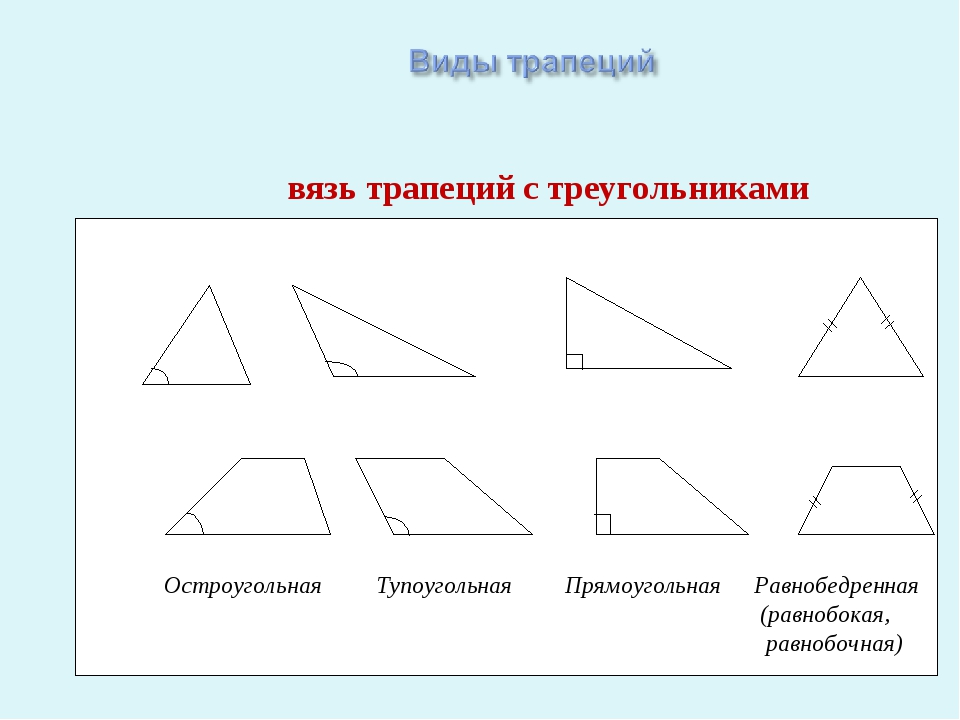
Связь трапеций с треугольниками Остроугольная Тупоугольная Прямоугольная Равнобедренная (равнобокая, равнобочная)

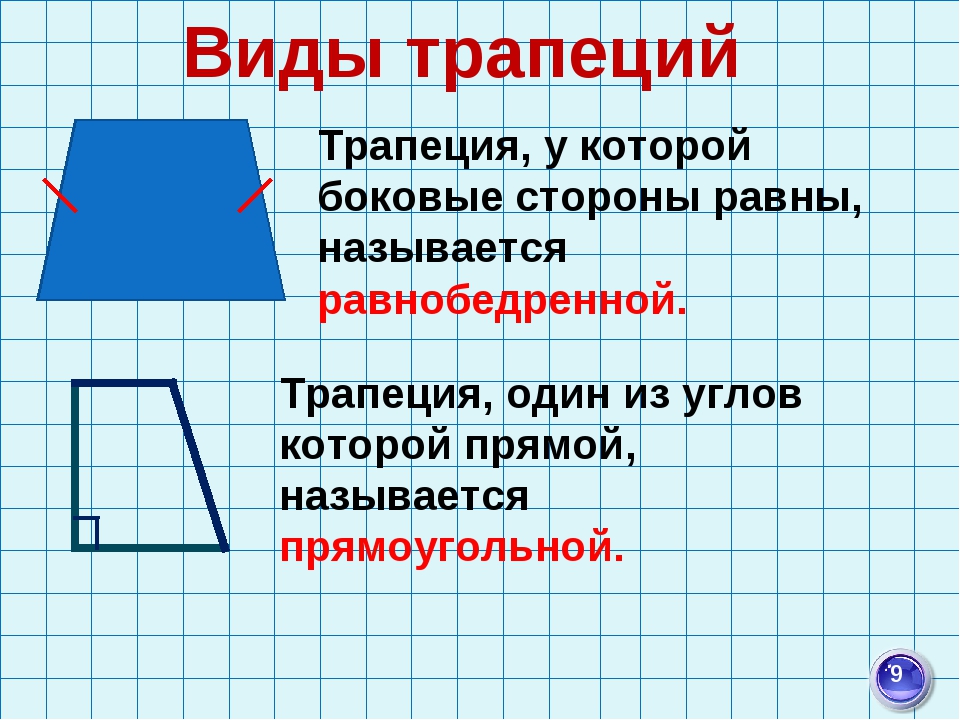
Виды трапеций Трапеция, у которой боковые стороны равны, называется равнобедренной. Трапеция, один из углов которой прямой, называется прямоугольной. 9

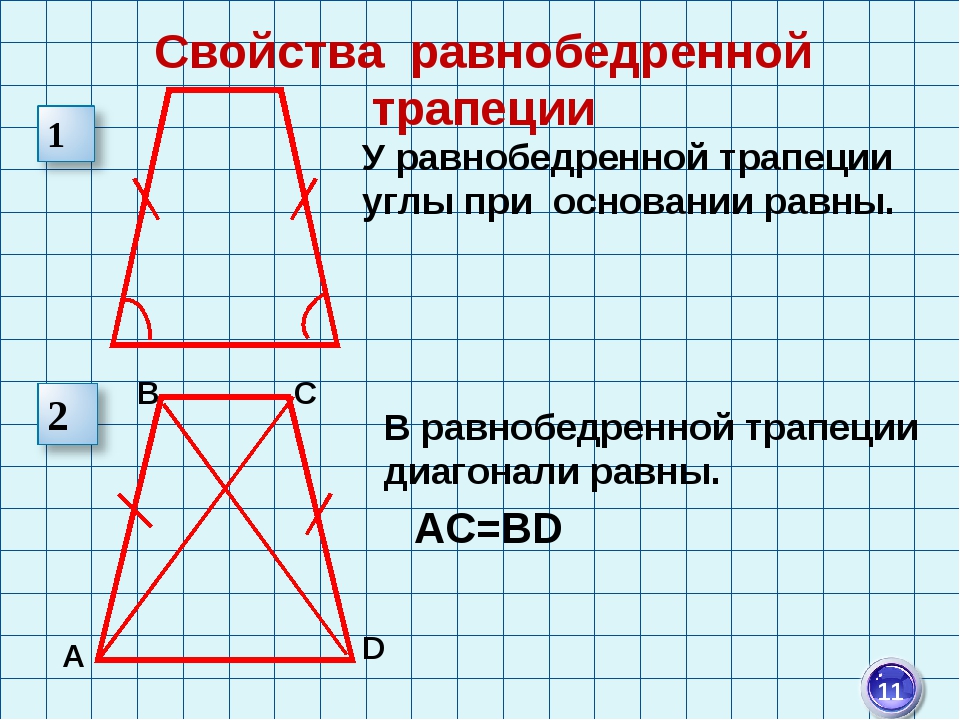
Свойства равнобедренной трапеции У равнобедренной трапеции углы при основании равны. В равнобедренной трапеции диагонали равны. А В С D АС=ВD 11

В A C D B1 Каким свойством обладают углы при основании равнобедренного треугольника? Какую гипотезу можно выдвинуть? 1) У равнобедренной трапеции углы при основании равны. C1 Дано: АВСD – равнобокая трапеция; АВ = СD. Доказать: Доказательство: Рассмотрим ∆АВВ1 и ∆DCC1 – прямоугольные. ∆АВВ1= ∆DCC1(по гипотенузе и катету: АВ = СD и ВВ1 = СС1.) =>

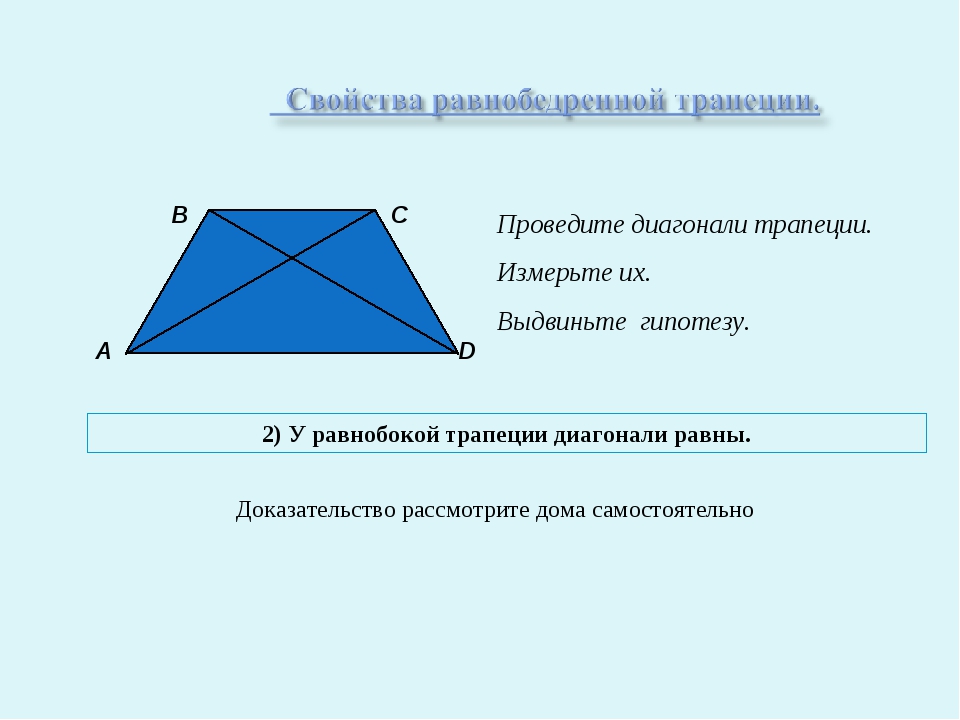
А В С D Проведите диагонали трапеции. Измерьте их. Выдвиньте гипотезу. 2) У равнобокой трапеции диагонали равны. Доказательство рассмотрите дома самостоятельно

Признаки равнобедренной трапеции Если углы при основании трапеции равны, то она равнобедренная. Если в трапеции диагонали равны, то она равнобедренная. 12

M N P Q Ответ : ∠M = 71°, ∠P = 143°. 13

A B C D Ответ: 115°, 65°,65° 14

A B C D Ответ : 22 см. 15

Дано: ABCD – трапеция, АD = 7, ВС = 5, АВ = CD. Найти: СD. Задача № 4. 16

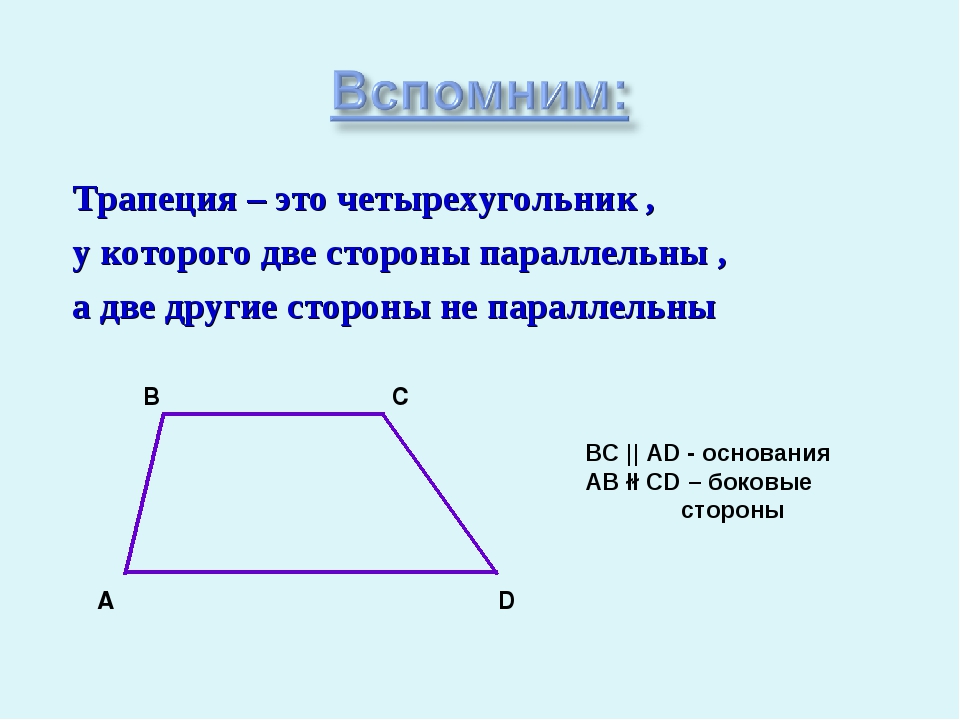
Трапеция – это четырехугольник , у которого две стороны параллельны , а две другие стороны не параллельны BC || AD - основания AB łł CD – боковые стороны

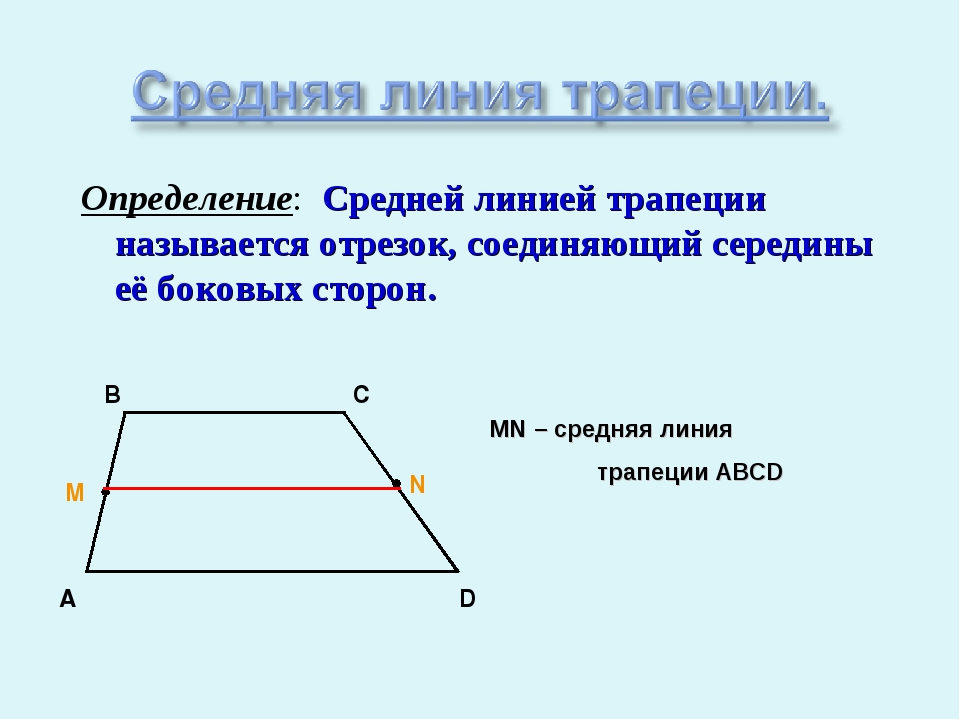
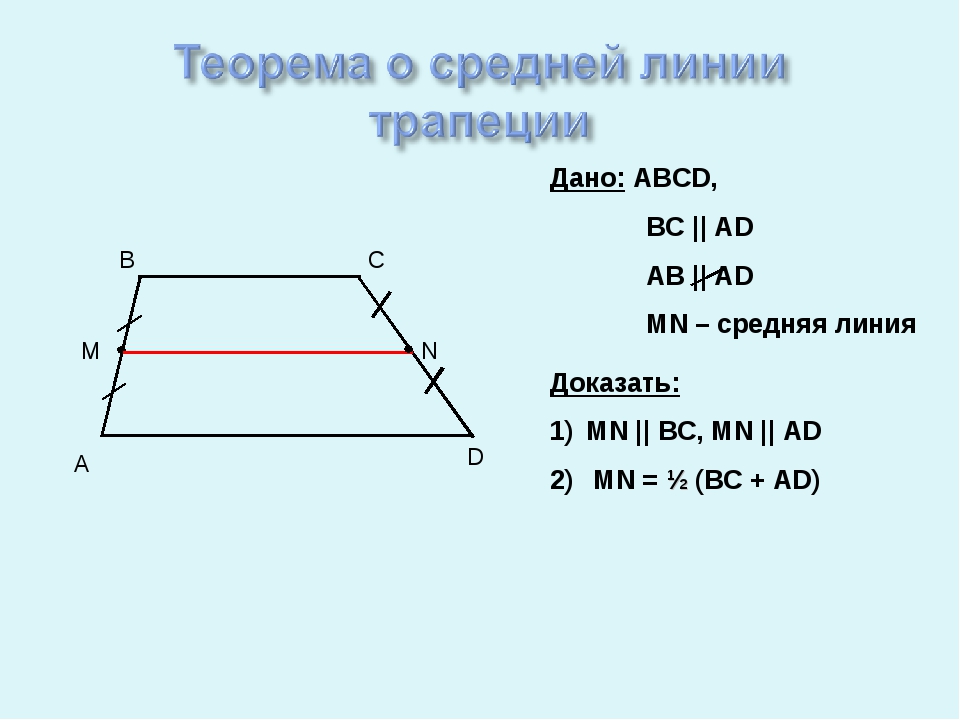
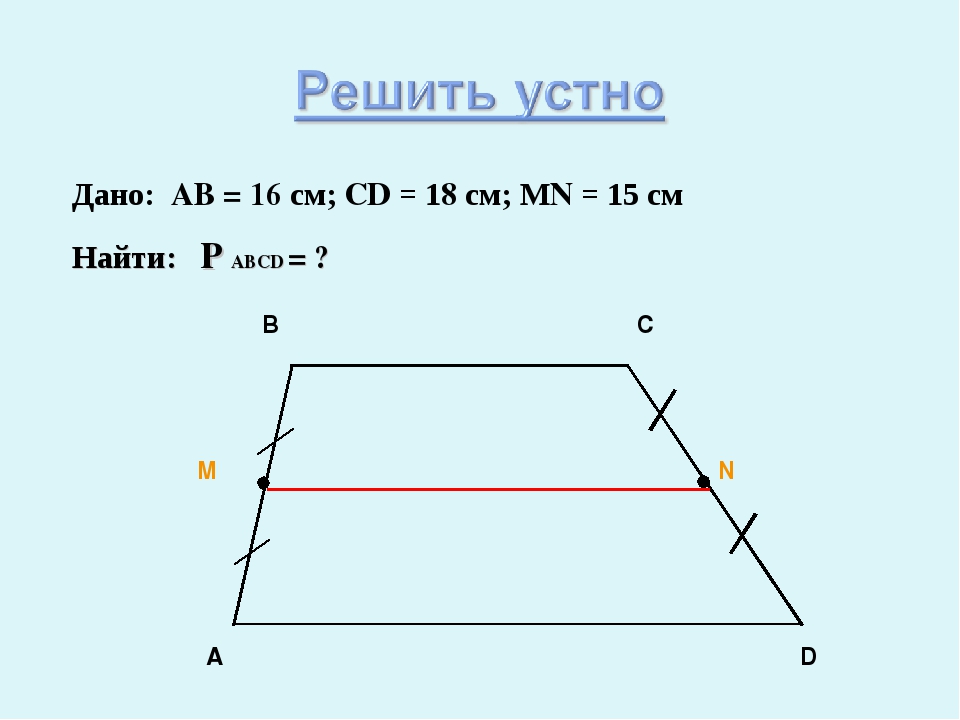
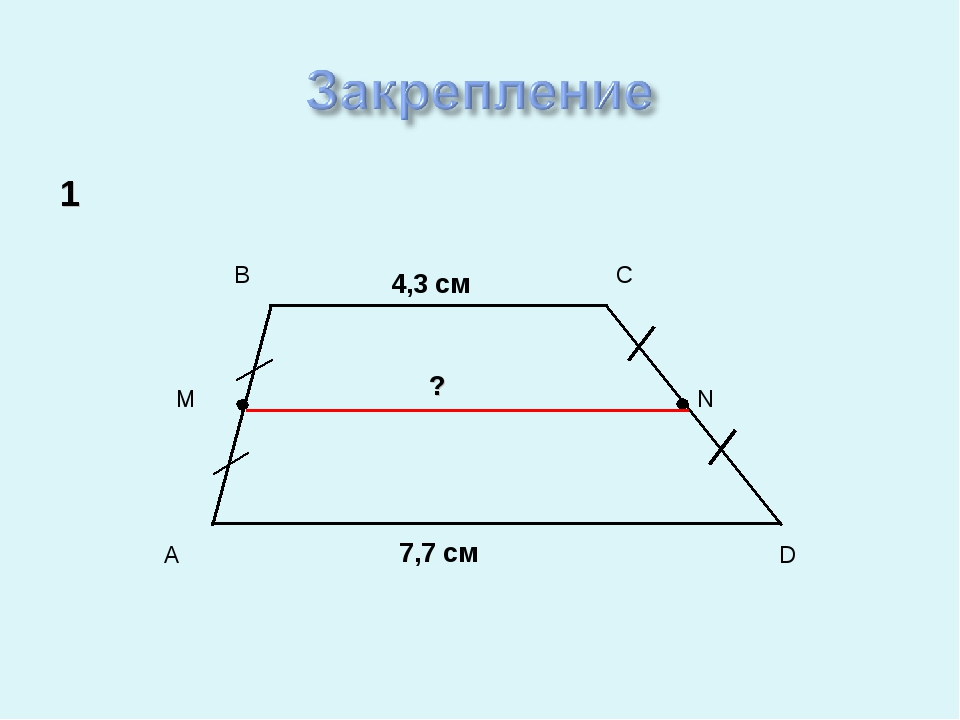
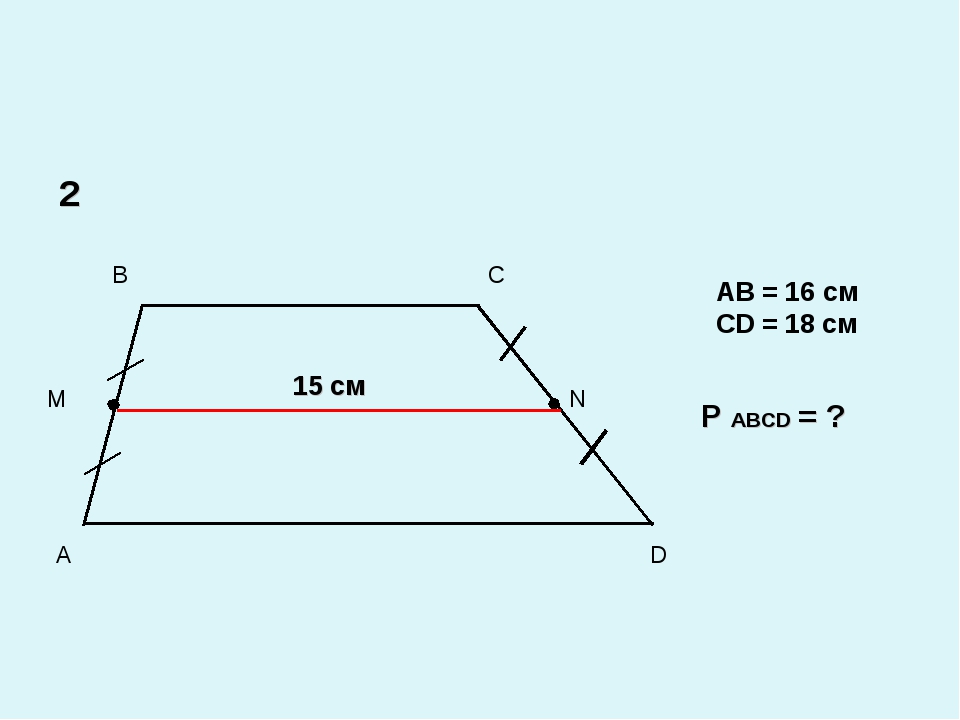
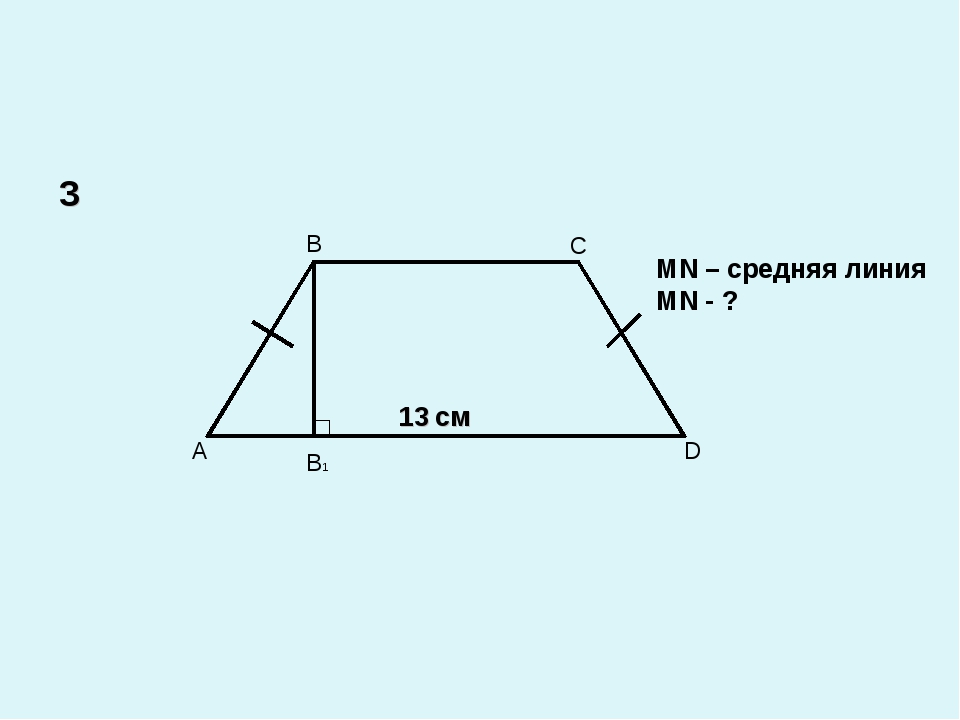
Определение: Средней линией трапеции называется отрезок, соединяющий середины её боковых сторон. MN – средняя линия трапеции ABCD

Средняя линия трапеции параллельна её основаниям и равна их полусумме.

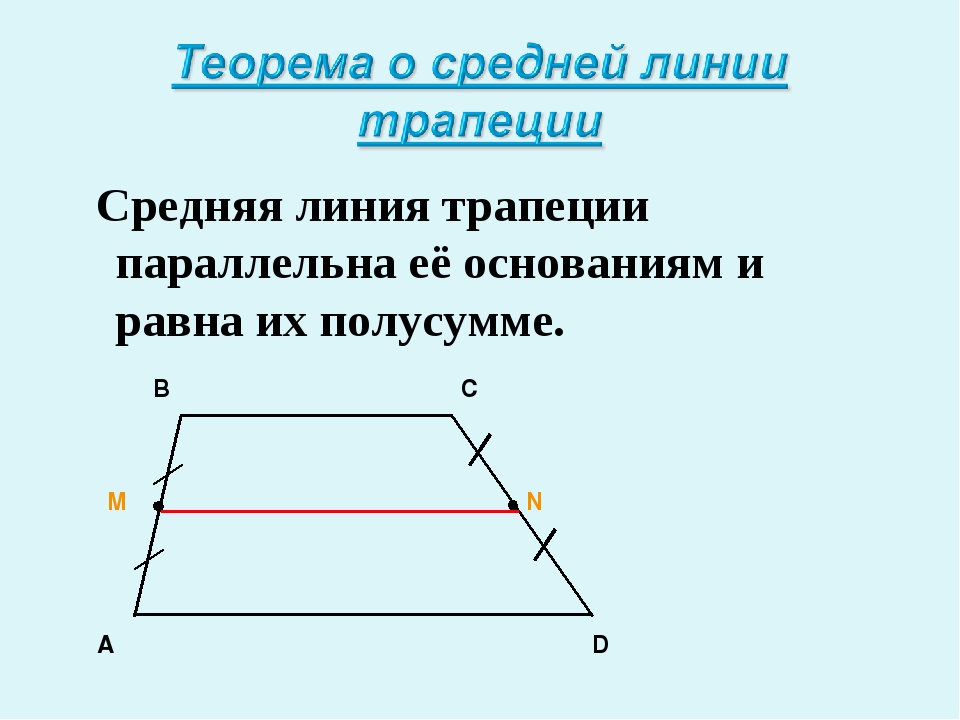
A D B C Дано: ABCD, BC || AD AB || AD MN – средняя линия Доказать: MN || BC, MN || AD MN = ½ (BC + AD)

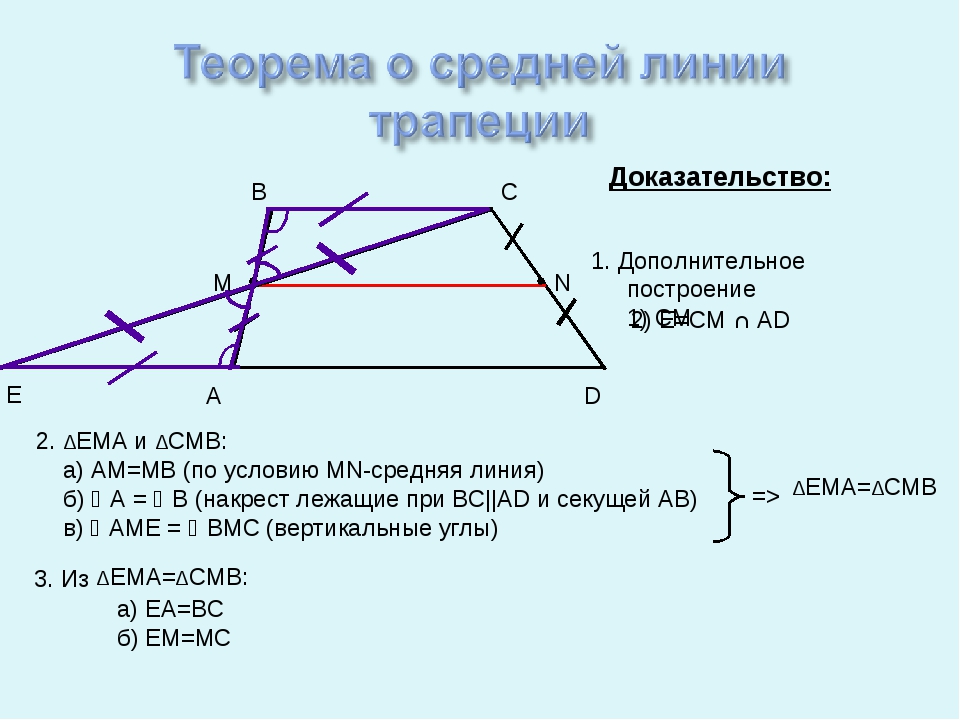
A D B C Доказательство: Е 1. Дополнительное построение 1) CM 2. ΔEMA и ΔCMB: а) AM=MB (по условию MN-средняя линия) б) A = B (накрест лежащие при BC||AD и секущей AB) в) AME = BMC (вертикальные углы) 2) E=CM ∩ AD а) EA=BC б) EM=MC

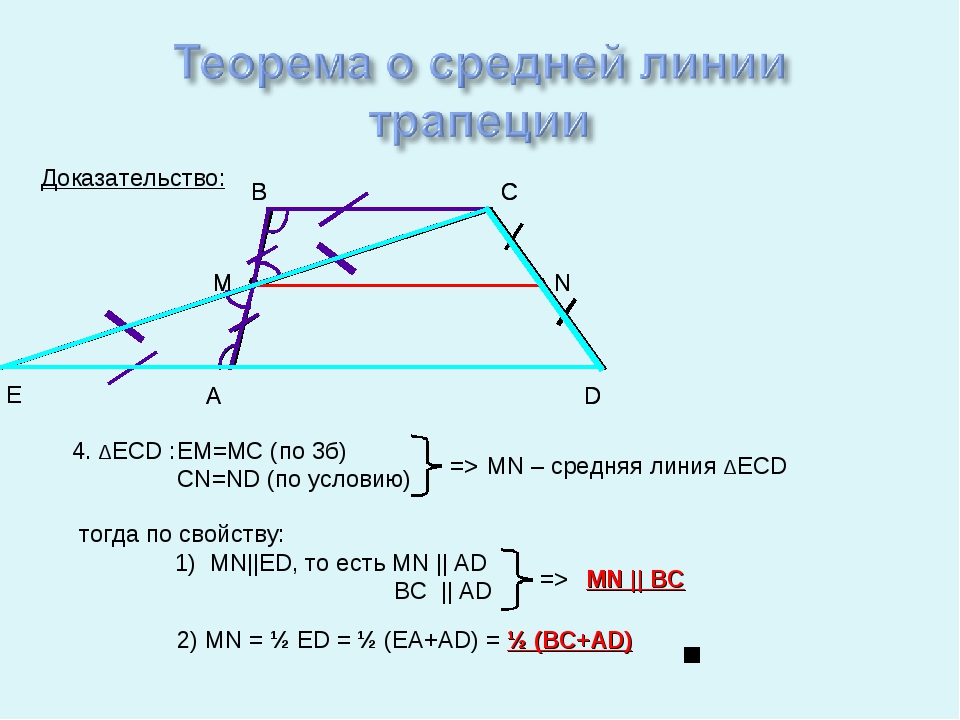
A D B C Доказательство: Е 4. ΔECD : EM=MC (по 3б) CN=ND (по условию) тогда по свойству: 1) MN||ED, то есть MN || AD BC || AD 2) MN = ½ ED = ½ (EA+AD) = ½ (BC+AD) A D B C Е

6,3 см 18,7 см ?

Дано: AB = 16 см; CD = 18 см; МN = 15 см Найти: P ABCD = ?

Дано: PΔ = 54; MN – средняя линия Найти: MN M N 7 5 ?

4,3 см 7,7 см ? 1

15 см AB = 16 см CD = 18 см P ABCD = ? 2

A B C D B1 13 см MN – средняя линия MN - ? 3

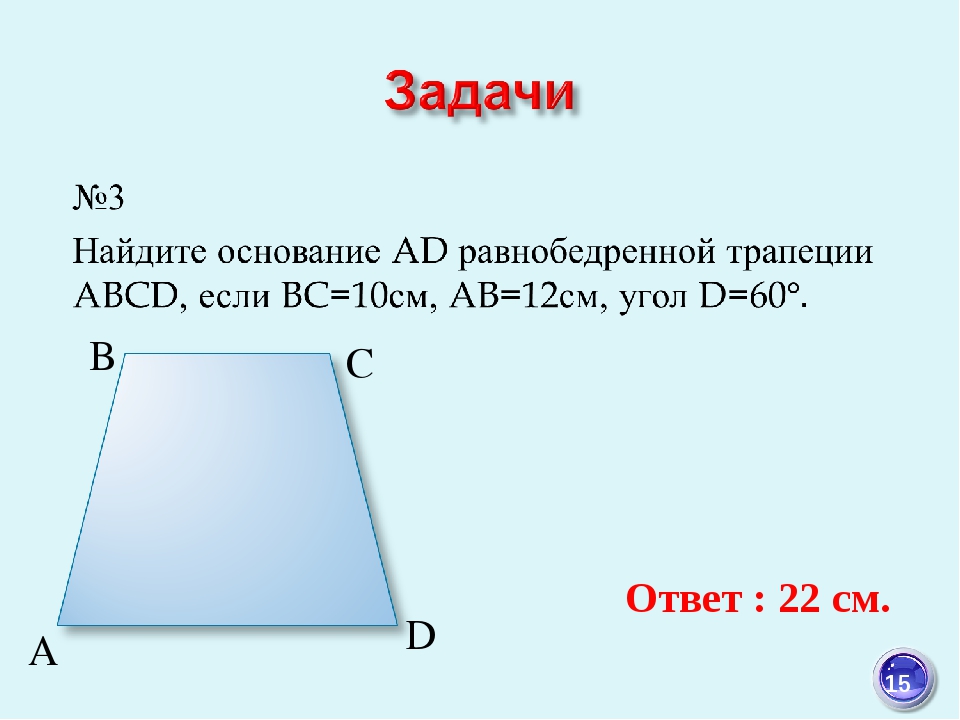
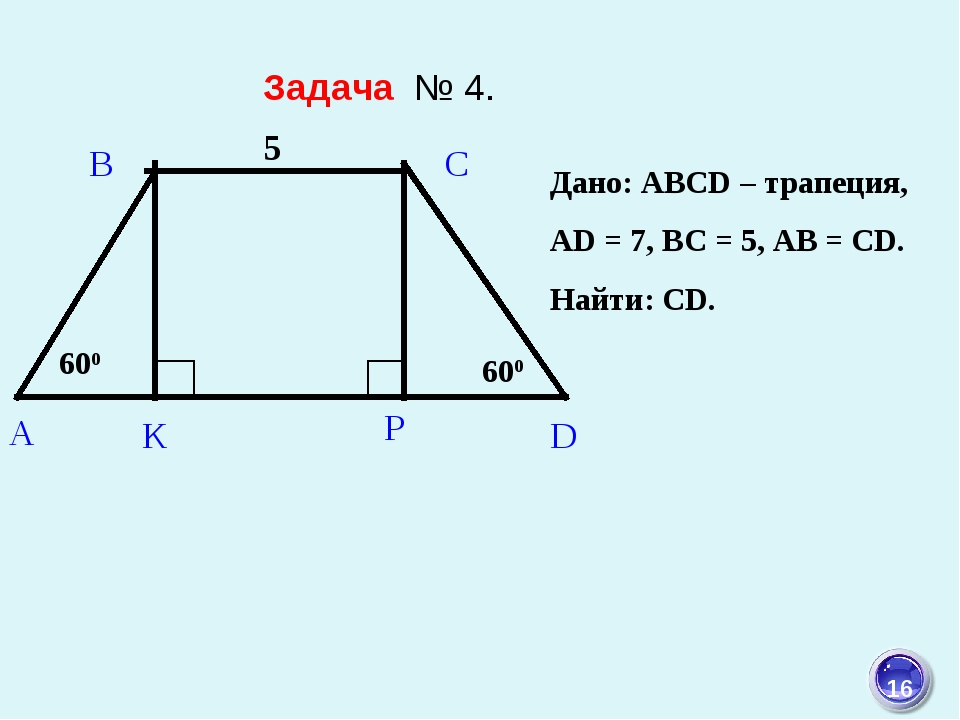
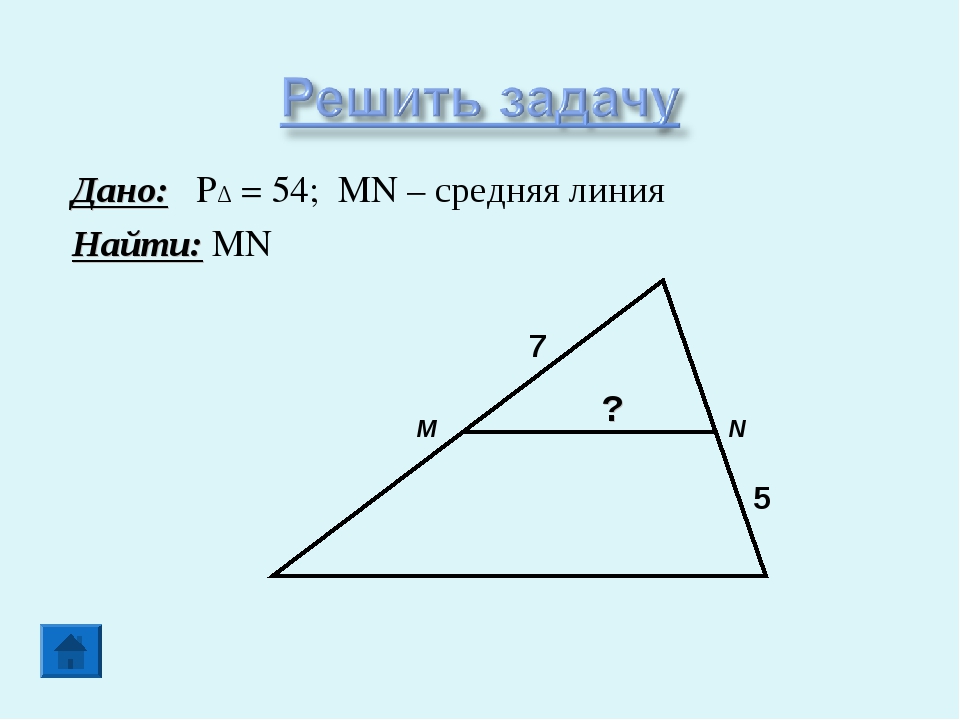
A D B C Решение: Sabcd = CE*(BC+AD)/2 CE = CD*cos(30) = CD*sin(60) CE = 20*(√3) /2 = 10 *(√3) Sabcd = 14 * 10 *(√3) = 140*(√3) 20 см E 60 30

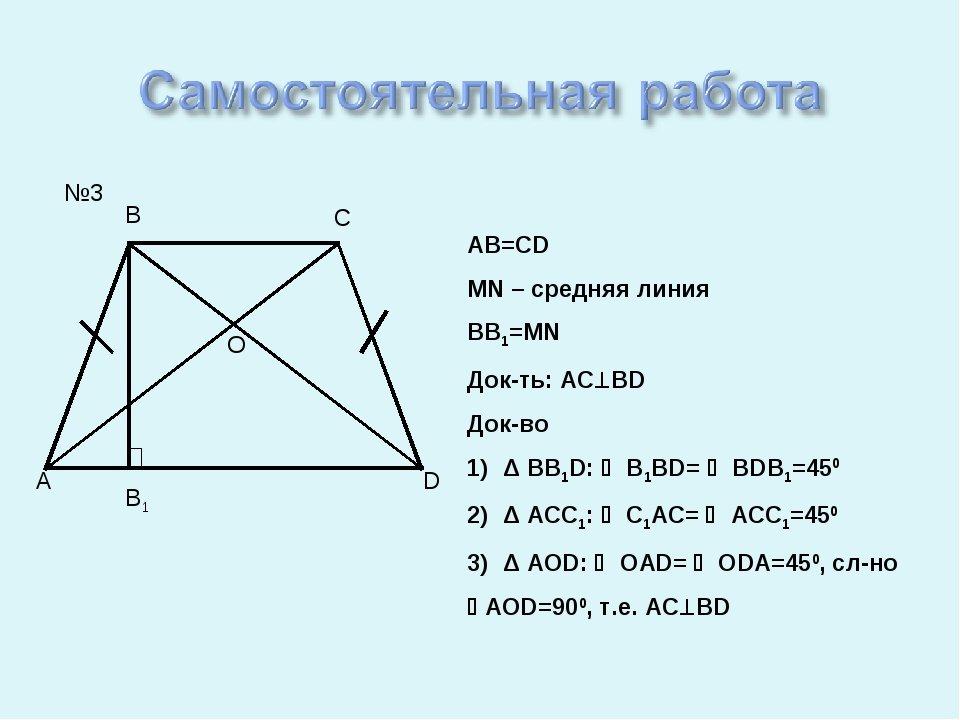
№3 AB=CD MN – средняя линия BB1=MN Док-ть: ACBD Док-во Δ BB1D:  B1BD=  BDB1=450 Δ ACC1:  C1AC=  ACC1=450 Δ AOD:  OAD=  ODA=450, сл-но AOD=900, т.е. ACBD

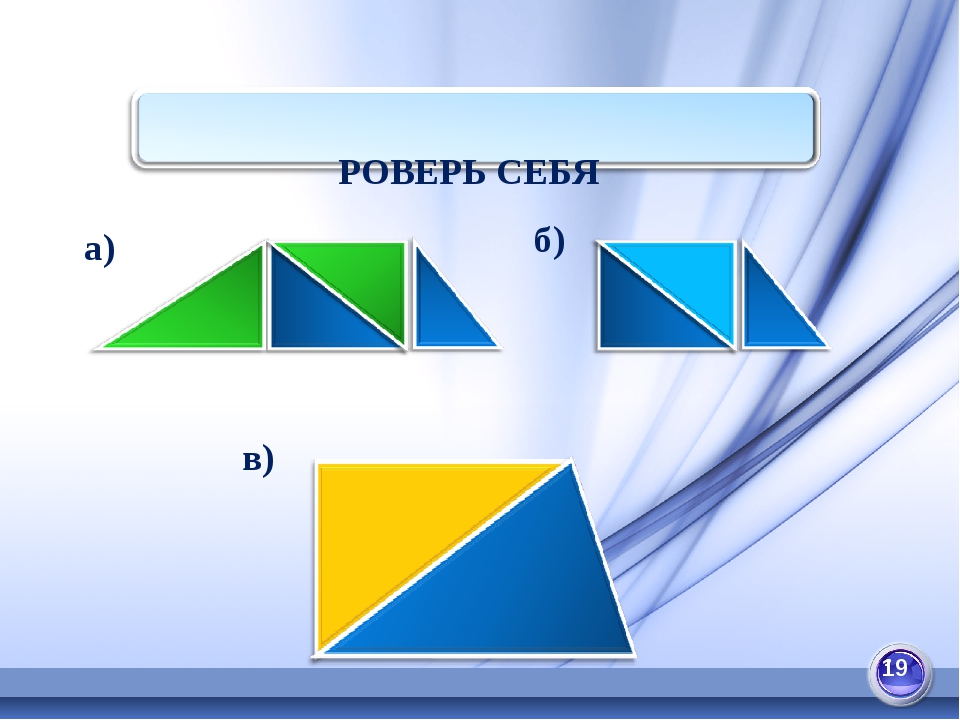
ЗАНИМАТЕЛЬНАЯ ЗАДАЧА Сложить трапецию из: а) четырёх прямоугольных треугольников; б) из трёх прямоугольных треугольников; в) из двух прямоугольных треугольников. Выяснить, каким условиям при этом должны удовлетворять данные трапеции. 18

ПРОВЕРЬ СЕБЯ 19

Оцените Ваше настроение * Чувствовали себя превосходно, на уроке всё поняли Работали на уроке хорошо, но не всё получалось Работали на уроке удовлетворительно, плохо всё поняли

№2 Найдите : x . a b c d 120° 60° x x + 10° Спасибо за внимание !