
Презентация "Построение прямых углов на местности"

Краткое описание документа:
В данном уроке речь пойдёт о практическом применении геометрии человеком, но для начала, вспомним необходимые теоретические утверждения. Рассмотрим частный случай смежных углов, то есть когда эти углы равны друг другу. Представим прямую «АС» с точкой «О» и прямую «ВО», которая входит в точку «О» под каким-то углом. Угол «АОВ» обозначим за «альфа», а угол «ВОС» обозначим за «бета». Сумма смежных углов равняется ста восьмидесяти градусам. Если эти углы равны между собой, то альфа и бета равны девяносто градусам. Действительно, их сумма равна ста восьмидесяти градусам, а углов двое, то есть мы сделали простейшее деление. Если два угла равняются девяносто градусов, то прямые «АС» и «ВО» перпендикулярны. Факт перпендикулярности записывается с помощью специального знака.

слайды 1-2 (Тема презентации "Построение прямых углов на местности", пример)
Итак, существует прямая, которая перпендикулярна другой прямой. Значит, существует много прямых, которые перпендикулярны данной прямой. Если несколько прямых перпендикулярны одной прямой, то они не имеют общих точек, потому что будут параллельны.
Сегодня мы поговорим о том, как данная особенность перпендикулярных прямых используется человеком в жизни. Перед тем, как мы перейдём к современным инструментам, подумаем о том, как математику использовали в Древнем Египте. Жители страдали от постоянного разлива Нила, и им необходимо было восстанавливать то, как выглядели земельные участки до. Как известно, египтяне были людьми не глупыми и они уже в то время знали, что треугольник, который имеет стороны размером 3,4 и 5, является прямоугольным. Даже сейчас мы слышим, как такой треугольник называют египетским. Так что же делали египтяне в случае с границами участков? Они делили верёвку на двенадцать равных частей, забивали колышек в узел и далее отмеряли сторону с длиною в три отрезка. После чего забивался колышек, и отмеряли сторону длиною в четыре отрезка. Так получали прямоугольный треугольник.
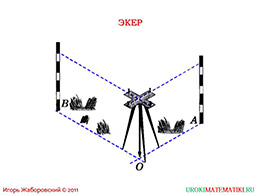
Современному человеку не приходится использовать верёвки и колышки, чтобы измерить прямой угол, потому что есть такое приспособление как экер или эккер.

слайды 3 (примеры, определение степени)
Это такой специальный топографический прибор, который позволяет разбить землю на прямые, пересекающиеся под углом девяносто градусов. Сам прибор содержит две перпендикулярные планки, которые прикрепляются к колу. Получается, человек сквозь прорез видит одно направление, а перпендикулярную плоскость видит в зеркальном отображении. Однако наиболее точным прибором, который используют ныне геодезисты, является теодолит. Именно его вы видите на слайде. Человека справа вы часто можете наблюдать у дорог и, скорее всего, задаётесь вопросом: «Что же он там делает?» Прибор собственно предназначен для геодезических работ, а его ценность в том, что он позволяет не только измерять расстояние, но и определять азимуты, то есть он полифункциональный, в отличие от монофункционального экера.
В завершении урока стоит повторить то, что прямые, перпендикулярные одной прямой не пересекаются, потому что являются параллельными. Напоследок, уточните в каких случаях, кроме дороги, может использоваться экер и теодолит.
| Автор | |
|---|---|
| Дата добавления | 02.08.2014 |
| Раздел | Геометрия |
| Подраздел | Презентация |
| Просмотров | 5353 |
| Номер материала | 238 |