Презентация к уроку геометрии в 10 классе "Аксиомы стереометрии"

























Описание презентации по отдельным слайдам:
Основные фигуры в пространстве: точка прямая плоскость α Обозначение: А; В; С; …; М;… а Обозначение: a, b, с, d…, m, n,…(или двумя заглавными латинскими) Обозначение: α, β, γ…
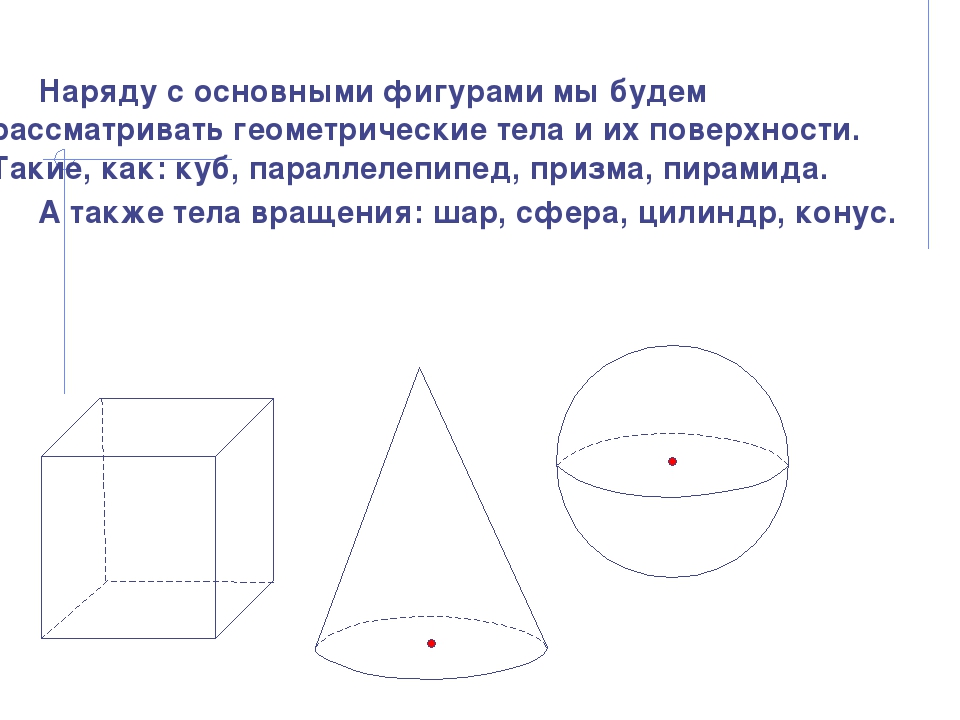
Наряду с основными фигурами мы будем рассматривать геометрические тела и их поверхности. Такие, как: куб, параллелепипед, призма, пирамида. А также тела вращения: шар, сфера, цилиндр, конус.
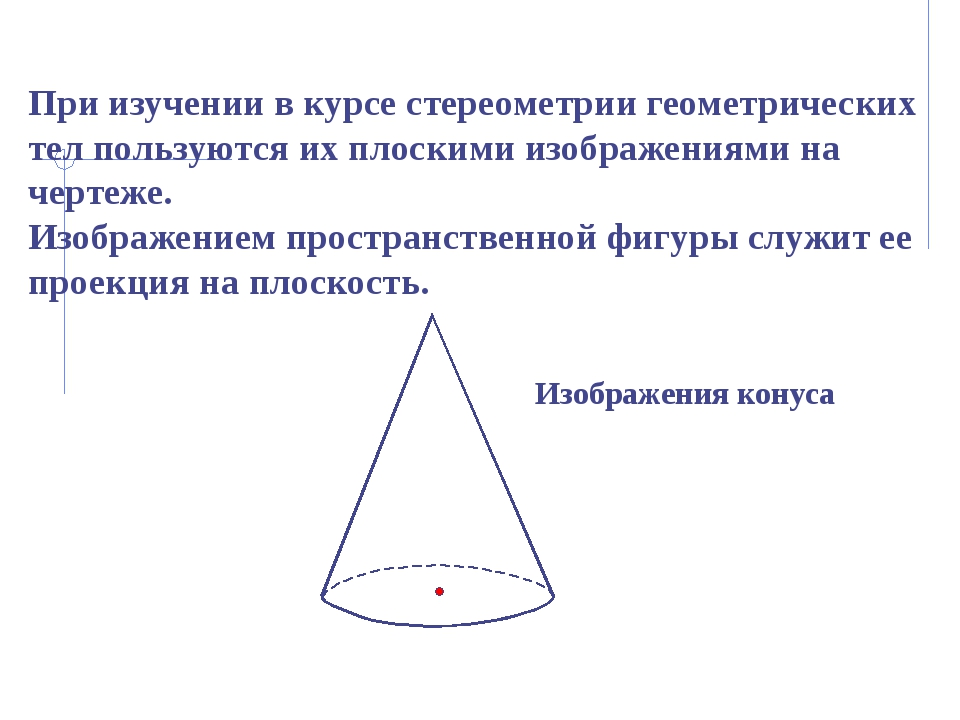
При изучении в курсе стереометрии геометрических тел пользуются их плоскими изображениями на чертеже. Изображением пространственной фигуры служит ее проекция на плоскость. Изображения конуса
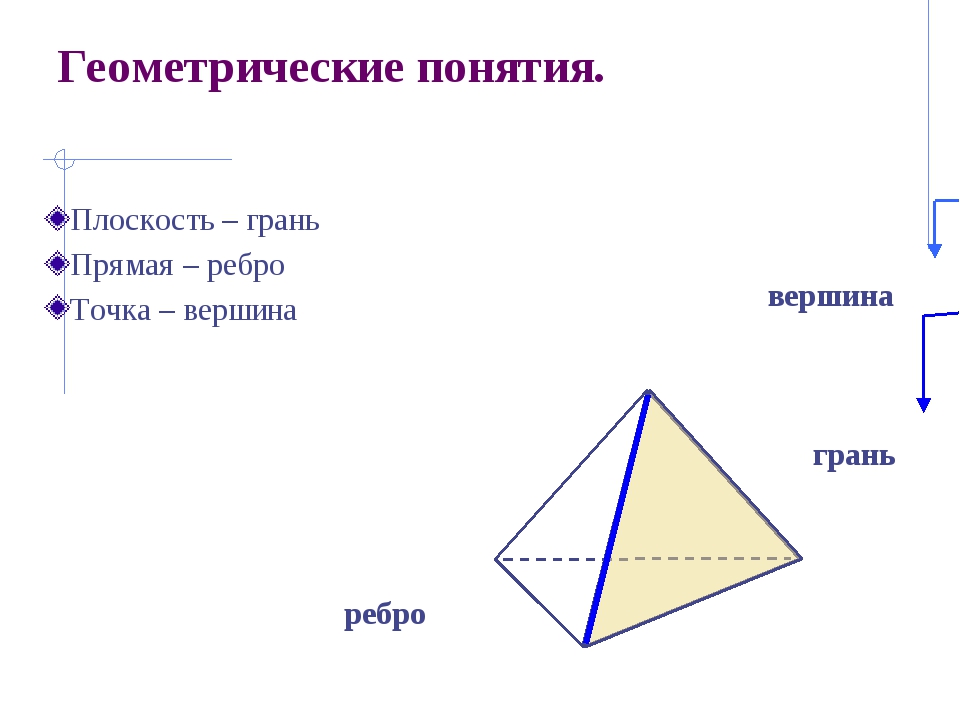
Геометрические понятия. Плоскость – грань Прямая – ребро Точка – вершина вершина грань ребро
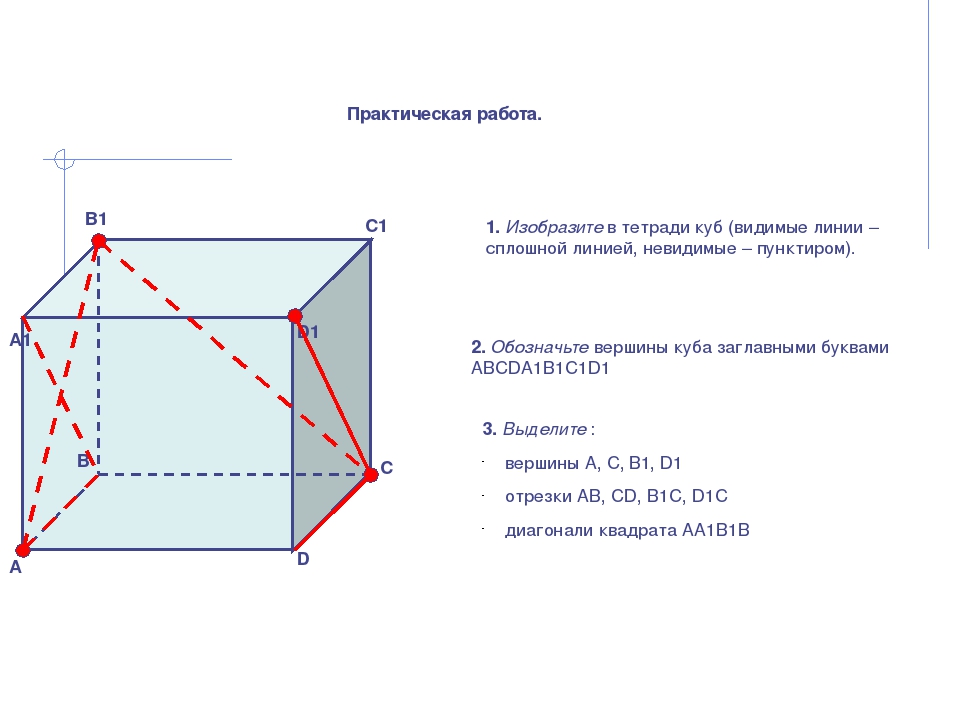
Практическая работа. 1. Изобразите в тетради куб (видимые линии – сплошной линией, невидимые – пунктиром). 2. Обозначьте вершины куба заглавными буквами АВСDА1В1С1D1 А В С D D1 С1 В1 А1 3. Выделите : вершины А, С, В1, D1 отрезки АВ, СD, В1С, D1С диагонали квадрата АА1В1В
Аксиома (от греч. axíõma – принятие положения) исходное положение научной теории, принимаемое без доказательства
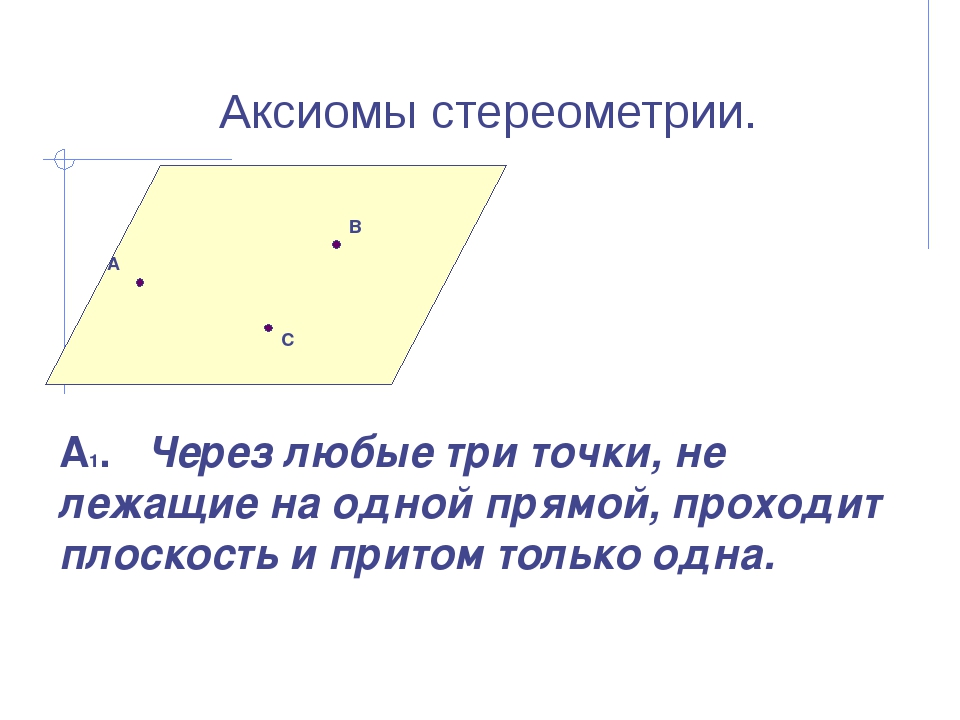
Аксиомы стереометрии. А В С А1. Через любые три точки, не лежащие на одной прямой, проходит плоскость и притом только одна. α
Самый простой пример к аксиоме А1 из повседневной жизни: Табурет с тремя ножками всегда идеально встанет на пол и не будет качаться. У табурета с четырьмя ножками бывают проблемы с устойчивостью, если ножки стула не одинаковые по длине. Табурет качается, т. е. опирается на три ножки, а четвертая ножка (четвертая «точка») не лежит в плоскости пола, а висит в воздухе.
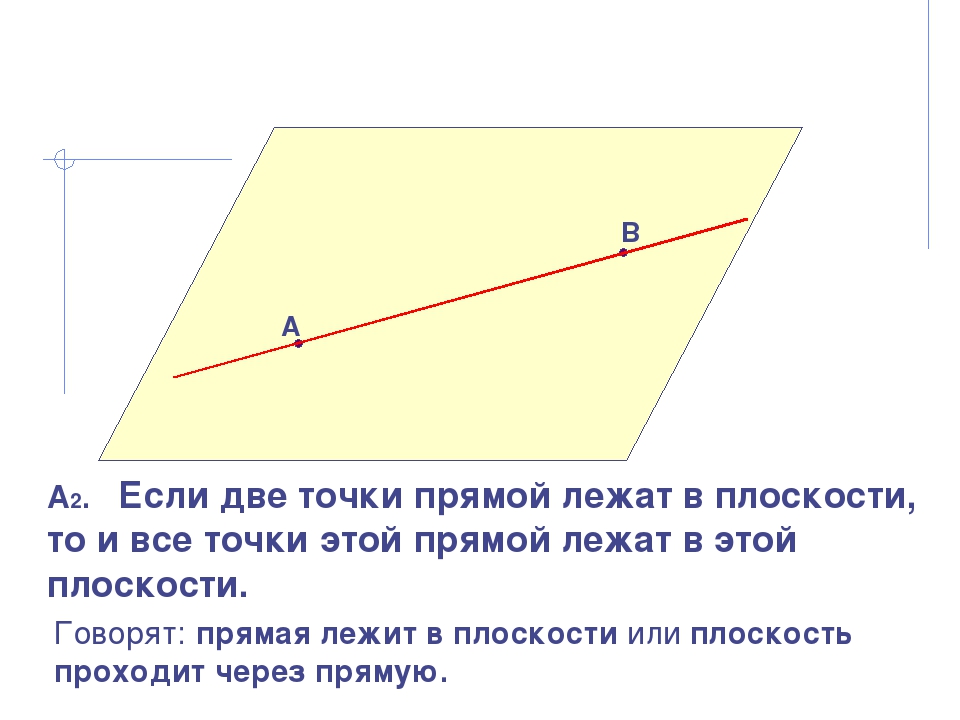
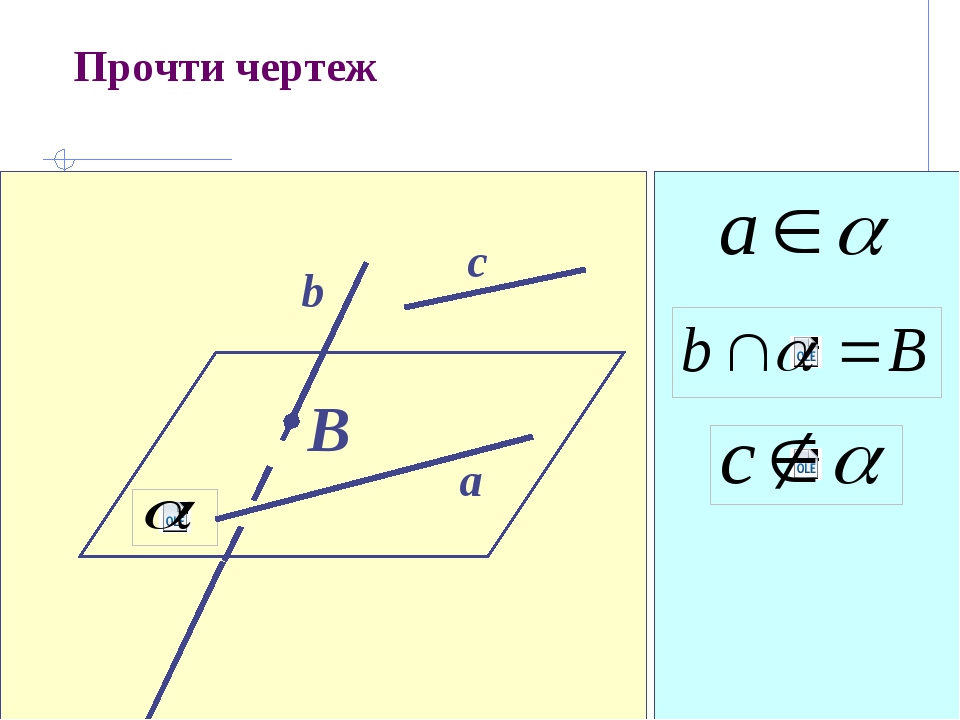
А В α А2. Если две точки прямой лежат в плоскости, то и все точки этой прямой лежат в этой плоскости. Говорят: прямая лежит в плоскости или плоскость проходит через прямую.
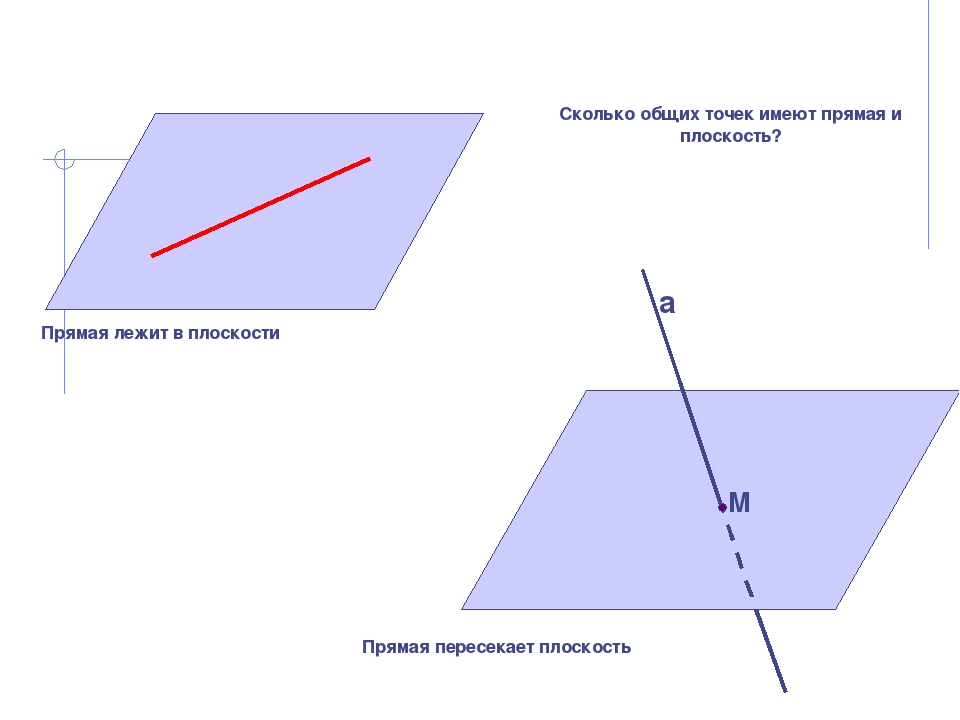
а М Прямая лежит в плоскости Прямая пересекает плоскость Сколько общих точек имеют прямая и плоскость?
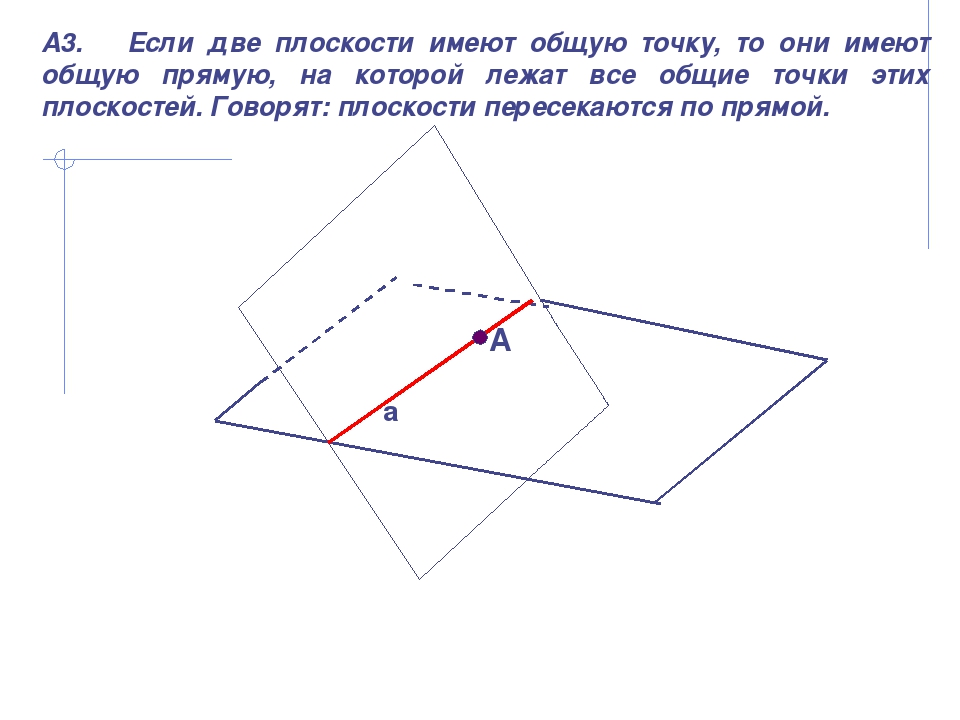
α β А3. Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей. Говорят: плоскости пересекаются по прямой. А а
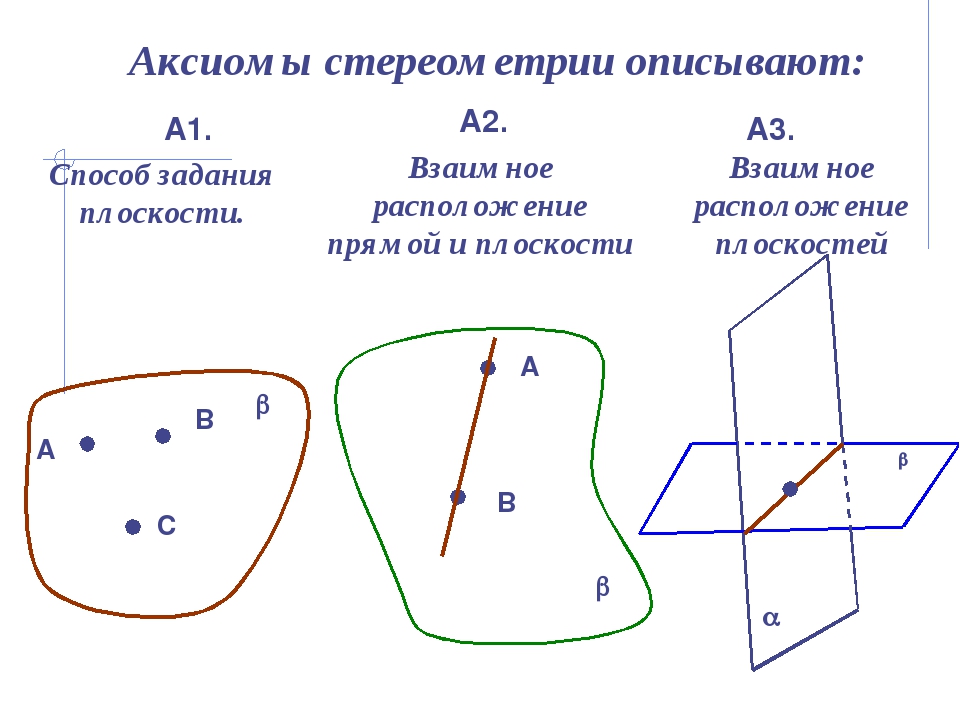
Аксиомы стереометрии описывают: А1. А2. А3. А В С b Способ задания плоскости. b А В Взаимное расположение прямой и плоскости a b Взаимное расположение плоскостей
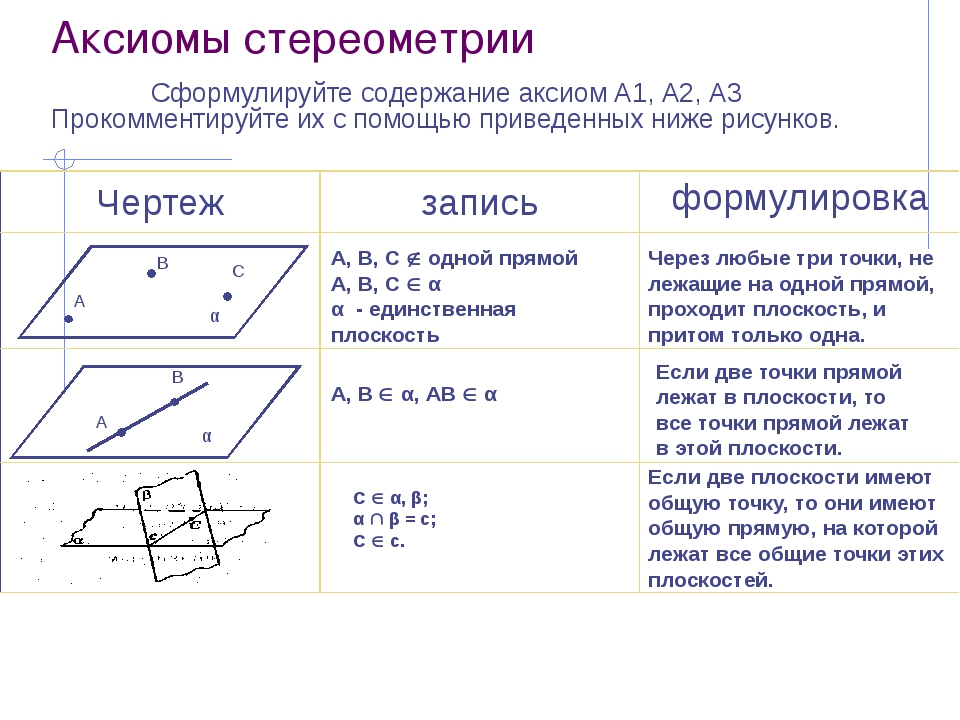
Аксиомы стереометрии Сформулируйте содержание аксиом А1, А2, А3 Прокомментируйте их с помощью приведенных ниже рисунков. α С В А α В А Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна. А, В, С одной прямой А, В, С α α - единственная плоскость Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости. А, В α, АВ α Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей. С α, β; α β = с; С с. Чертеж запись формулировка
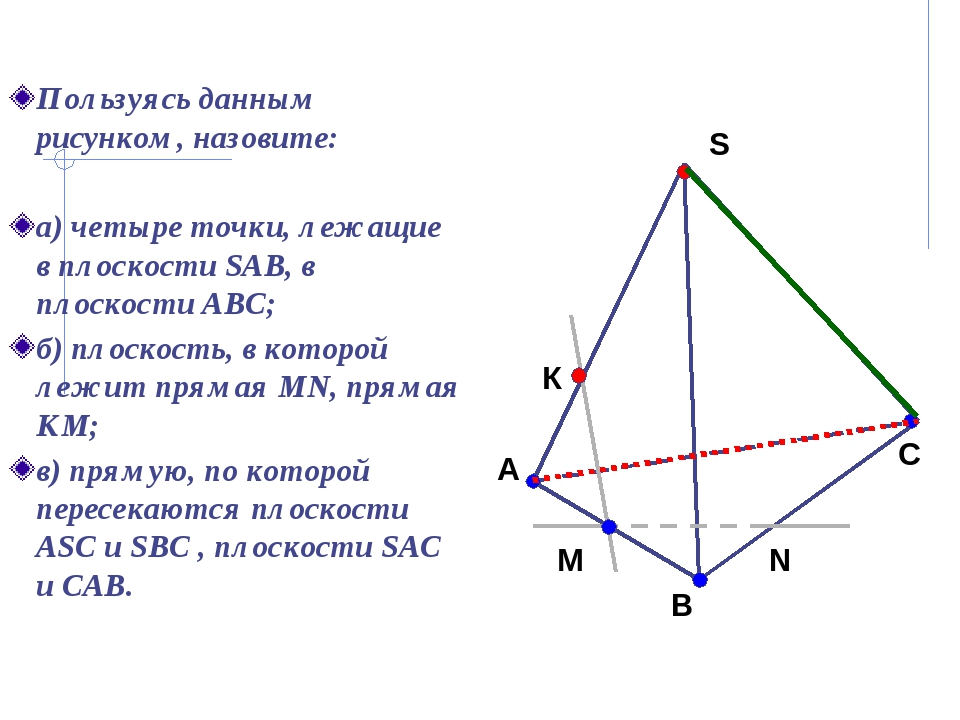
Пользуясь данным рисунком, назовите: а) четыре точки, лежащие в плоскости SAB, в плоскости АВС; б) плоскость, в которой лежит прямая MN, прямая КМ; в) прямую, по которой пересекаются плоскости ASC и SBC , плоскости SAC и CAB. К А В М S N C
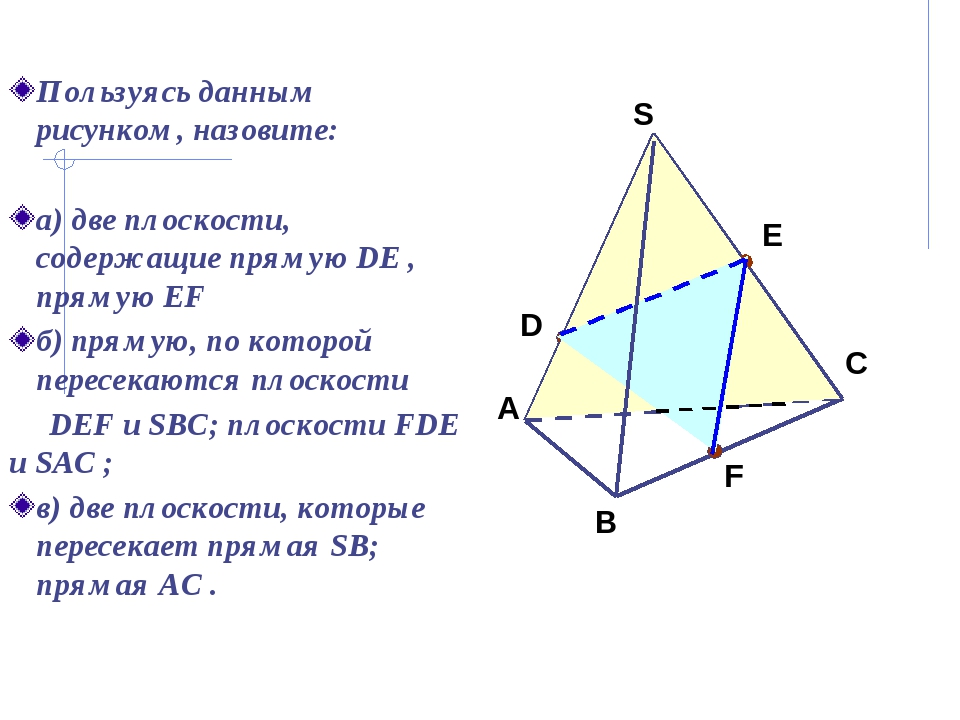
Пользуясь данным рисунком, назовите: а) две плоскости, содержащие прямую DE , прямую EF б) прямую, по которой пересекаются плоскости DEF и SBC; плоскости FDE и SAC ; в) две плоскости, которые пересекает прямая SB; прямая AC . А С
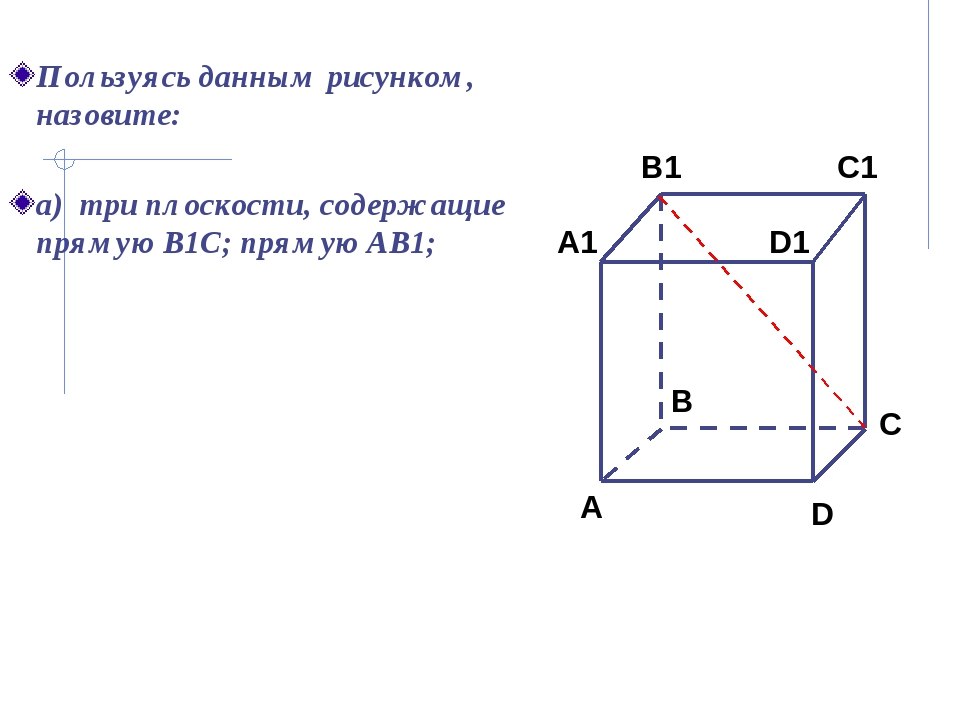
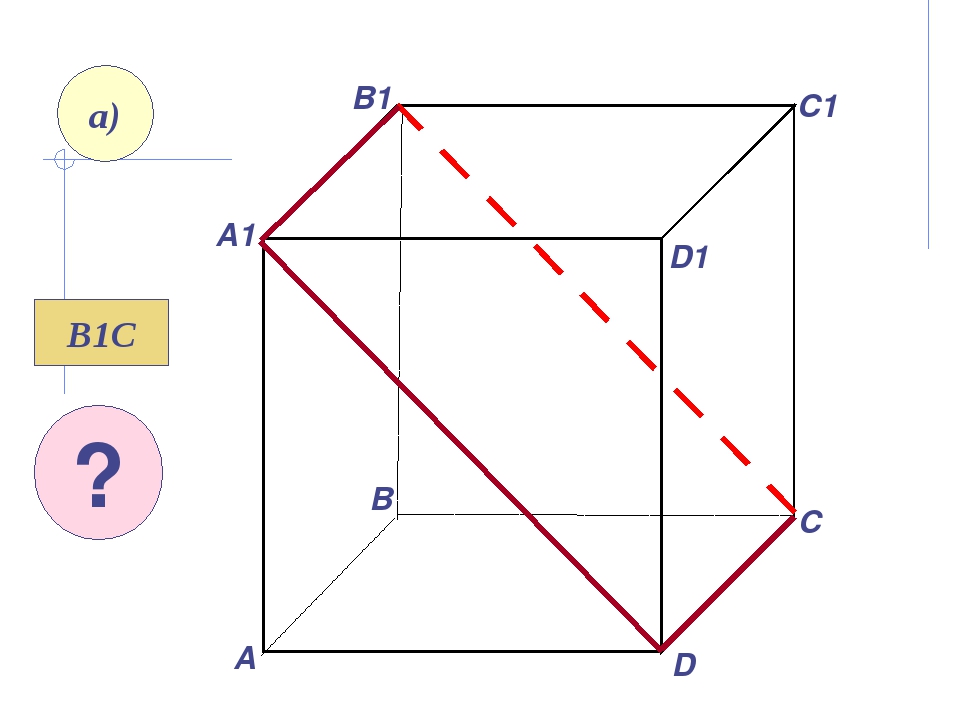
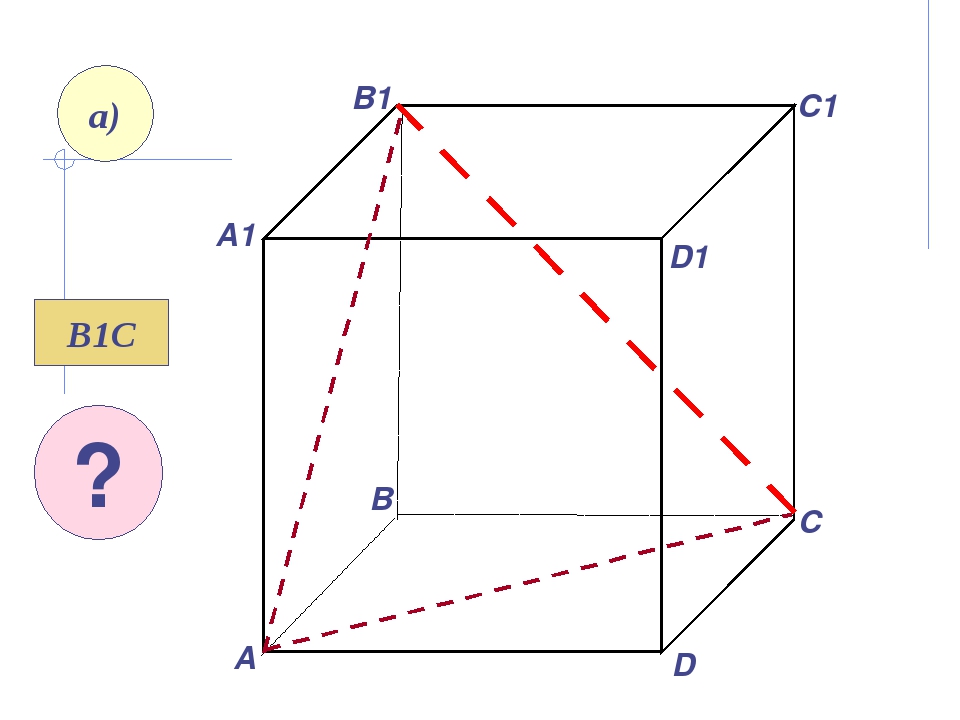
Пользуясь данным рисунком, назовите: а) три плоскости, содержащие прямую В1С; прямую АВ1; C1 C A1 B1 D1 A B D

| Автор | |
|---|---|
| Дата добавления | 07.01.2019 |
| Раздел | Геометрия |
| Подраздел | Презентация |
| Просмотров | 3528 |
| Номер материала | 6029 |