
Презентация "Неравенство треугольника"

Краткое описание документа:
В данном уроке мы познакомимся с неравенством треугольников и следствием из него. Данная фигура является основной в курсе геометрии, поэтому необходимо быть максимально внимательным, в ином случае пропущенный пласт знаний сыграет важную роль на появлении огромной пропасти в геометрии для вас. Неравенство треугольника вытекает из важной теоремы о сторонах и углах треугольника, которую следует повторить. Против большей стороны в треугольнике лежит больший угол и, наоборот, против большего угла лежит большая сторона.

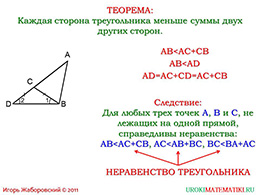
слайды 1-2 (Тема презентации "Неравенство треугольника", теорема)
Теперь необходимо визуализировать теорию, поэтому представим треугольник «АВС», где сторона «АВ» - самая большая. Значит, против этой стороны будет лежать самый большой угол, то есть угол «С» - самый большой. В общем виде: если отрезок «АВ» больше, чем отрезок «АС» и больше чем отрезок «ВС», то угол «С» больше угла «В» и больше угла «А». Именно из этой теоремы мы и докажем неравенство треугольника.
Данная теорема справедлива для всех сторон любого треугольника. Более того, она справедлива для всех видов треугольника: остроугольного, тупоугольного, прямоугольного. Однако сейчас мы говорим о произвольных треугольниках. Из теоремы о сумме сторон треугольника вытекает аналогичная теорема о разности сторон фигуры, но подробнее мы остановимся именно на первой, потому что они идентичны по процессу решения. Именно поэтому, решить вторую теорему – самостоятельное задание для учащихся на дом.
Сформулируем центральную теорему урока, которую видим перед нами. Она гласит о том, что любая сторона нашей фигуры будет меньше суммы оставшихся сторон. Получается в нашем треугольнике «ABС» даже самая длинная сторона «AВ» должна быть меньше суммы «AС» и «BС».
Доказательство заключается в следующем. Во-первых, мы проводим на прямой «АС» далее отрезок «СD», который равен отрезку «СВ». То есть у нас теперь новый равнобедренный треугольник «DСВ». В нём угол один равен углу два. Теперь в треугольнике «АВD» необходимо доказать, что «АВ» меньше «АD». Можно сравнить стороны треугольника, но для более лёгкого способа можно сравнить углы. По исходным данным угол два равен углу один, а поэтому меньше угла «АВD». А мы помним, что в треугольнике против большей стороны лежит большая сторона, а против меньшей – меньшая. Получаем, что «АВ» меньше «АD», а «АD» равняется «АС» плюс «СВ». То есть, теорема доказана.
Сегодня мы углубились в тему неравенства треугольника и рассмотрели одну из основополагающих теорем в геометрии.
| Автор | |
|---|---|
| Дата добавления | 02.08.2014 |
| Раздел | Геометрия |
| Подраздел | Презентация |
| Просмотров | 5405 |
| Номер материала | 261 |