
Урок "Теорема о сумме углов треугольника"

Краткое описание документа:
Видеоурок «Теорема о сумме углов треугольника» содержит доказательство одной из наиболее важных теорем геометрии – теоремы о сумме углов треугольника. Задача данного видеоурока – облегчить понимание и запоминание данной теоремы и ее доказательства.
Видеоурок может быть применен учителем для подачи нового материала на уроке по данной теме. Данный видеоматериал заменяет объяснение учителя и освобождает его для более качественного выполнения задач дифференцированного и индивидуального подхода в обучении. Доказательство теоремы проводится с использованием анимационных эффектов, «оживляющих» изображение и улучшающих качество восприятия материала учениками.
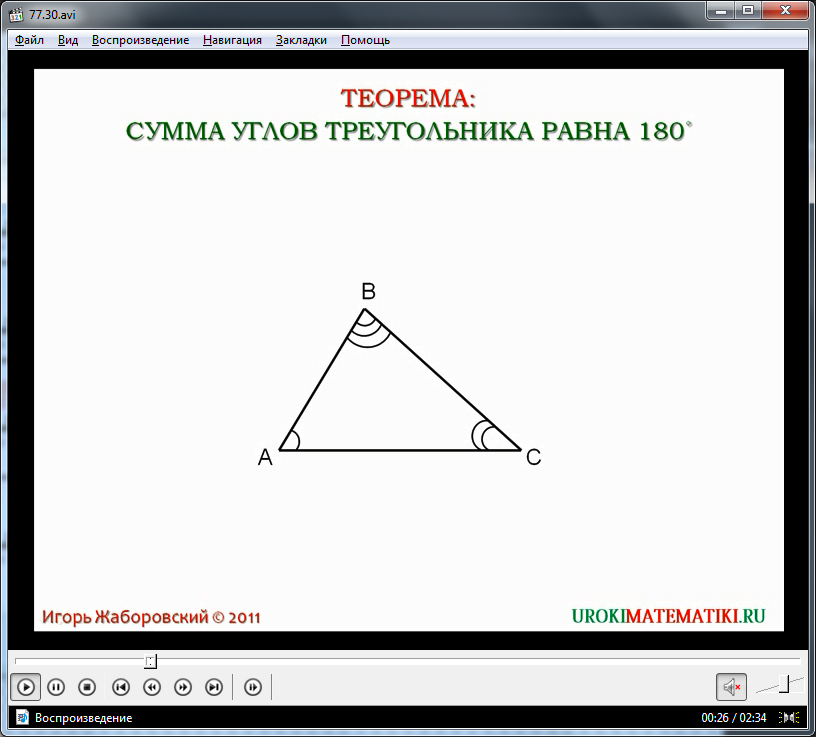
Видеоурок начинается с объявления названия темы. На экране отображается текст теоремы, утверждающей, что сумма углов любого треугольника равна 180°. Доказательство данной теоремы начинается с построения треугольника, на примере которого будет показан ход рассуждений. На рисунке построен треугольник ΔАВС, в котором отмечены ∠А, ∠В, ∠С. Необходимо доказать, что сумма величин углов будет 180°.
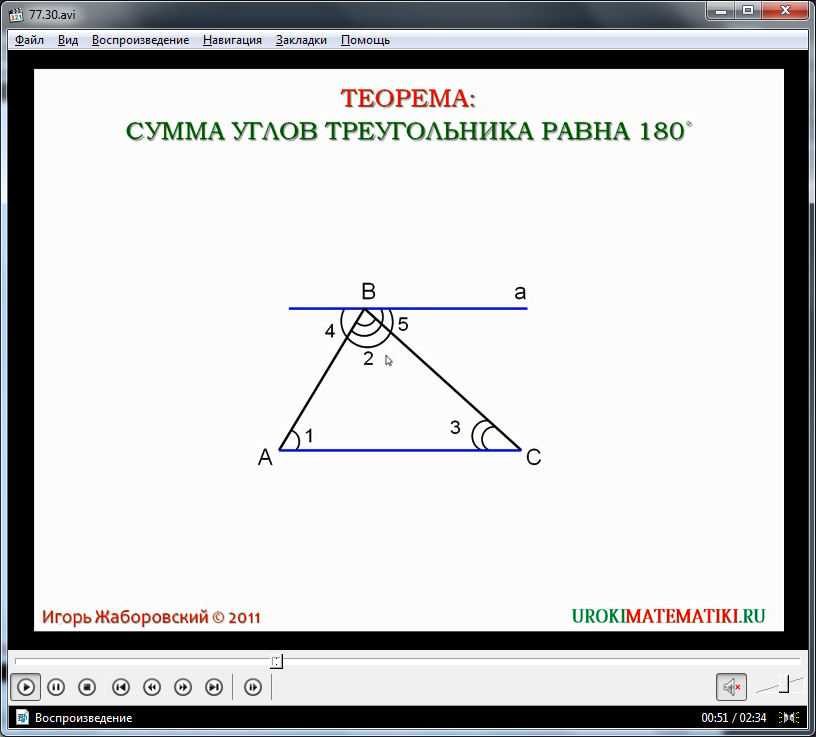
Для доказательства проводится дополнительная прямая а, проходящая через вершину В, и при этом параллельная стороне треугольника АС. Отмечаются внутренние углы треугольника, обозначенные ∠1, ∠2, ∠3, и образованные между прямой a и сторонами имеющегося треугольника СВ и АВ – углы ∠4, ∠5. Так как прямая а с прямой, содержащей АС, параллельны, то углы ∠1, ∠4 - накрест лежащие по отношению к секущей АВ и равные при построении. А углы ∠3, ∠5 - накрест лежащие при данных параллельных прямых по отношению к секущей ВС и равными между собой. На рисунке хорошо видно, что ∠4, ∠2, ∠5 в сумме составляют развернутый угол, равный 180°. Зная, что ∠1=∠4, а ∠3=∠5, подставляем в сумму углов ∠4+∠2+∠5 соответствующие значения внутренних углов. Получается, что сумма ∠1+∠2+∠3 равна 180°. Утверждение доказано.
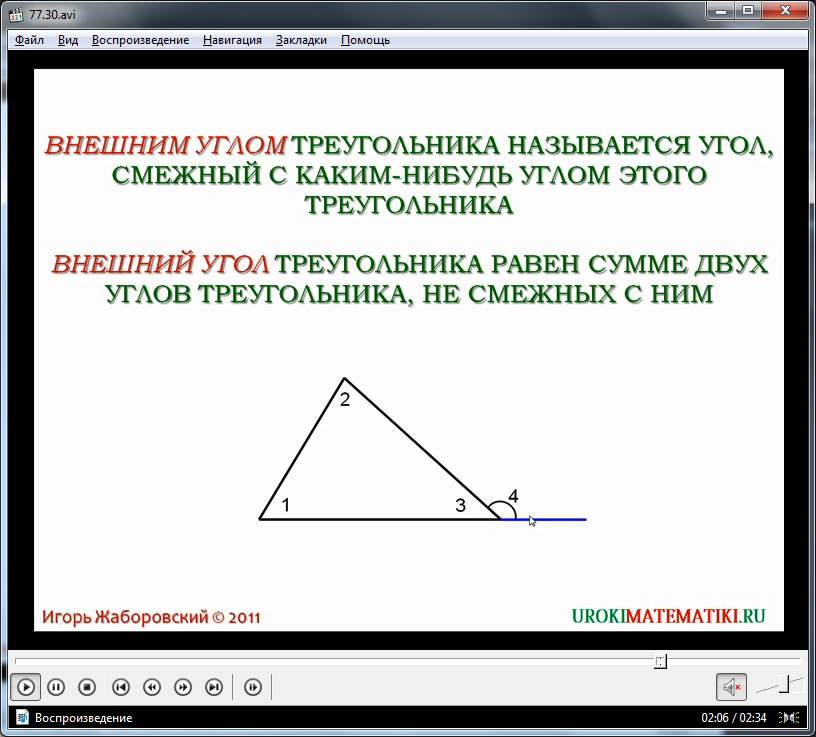
Далее в данном видеоуроке дается понятие внешнего угла треугольника и важное свойство, связанное с внешним углом. На экране отображается определение внешнего угла треугольника как угла, смежного с любым из углов данного треугольника. Определение выделено цветом и может быть предложено для записи учениками. Под определением дается важное свойство внешнего угла, утверждающее, что внешний угол треугольника будет равен сумме его не смежных углов. Для доказательства данного утверждения под текстом утверждения нарисован треугольник с углами, обозначенными ∠1, ∠2, ∠3, а также построен угол ∠4, смежный с углом ∠3. Так как углы ∠4, ∠3 смежные, то в сумме они составляют ∠4+∠3=180°. Из теоремы известно, что сумма углов в любом треугольнике 180°. Сравнивая два выражения видно, что из них следует ∠4=∠1+∠2. Это и есть искомое равенство. Теорема доказана.
Видеоурок «Теорема о сумме углов треугольника» подробно и понятно описывает доказательство теоремы, поэтому может быть рекомендован не только как наглядное пособие на уроке в школе, но и для самостоятельного рассмотрения темы учеником, а также может быть полезным учителю в дистанционном обучении.
| Автор | |
|---|---|
| Дата добавления | 02.08.2014 |
| Раздел | Геометрия |
| Подраздел | Видеоурок |
| Просмотров | 5595 |
| Номер материала | 517 |