
Урок "Теорема о соотношениях между сторонами и углами треугольника"

Краткое описание документа:
Видеоурок «Теорема о соотношениях между сторонами и углами треугольника» представляет данную теорему, а также следствия из нее. Знание теоремы и ее следствий необходимо для решения практических задач по геометрии, в которых для нахождения параметров треугольника используются различные соотношения его сторон и углов. Задача видеоурока – облегчить понимание материала, способствовать запоминанию теоремы и следствий из нее.
В видеоуроке использованы анимационные эффекты, которые помогают выделить важные детали геометрических фигур при усвоении материала. Также используется выделение цветом для выделения утверждения теоремы и ее следствий. Голосовое сопровождение объяснение полностью заменяет учителя при стандартной подаче ученикам нового материала.
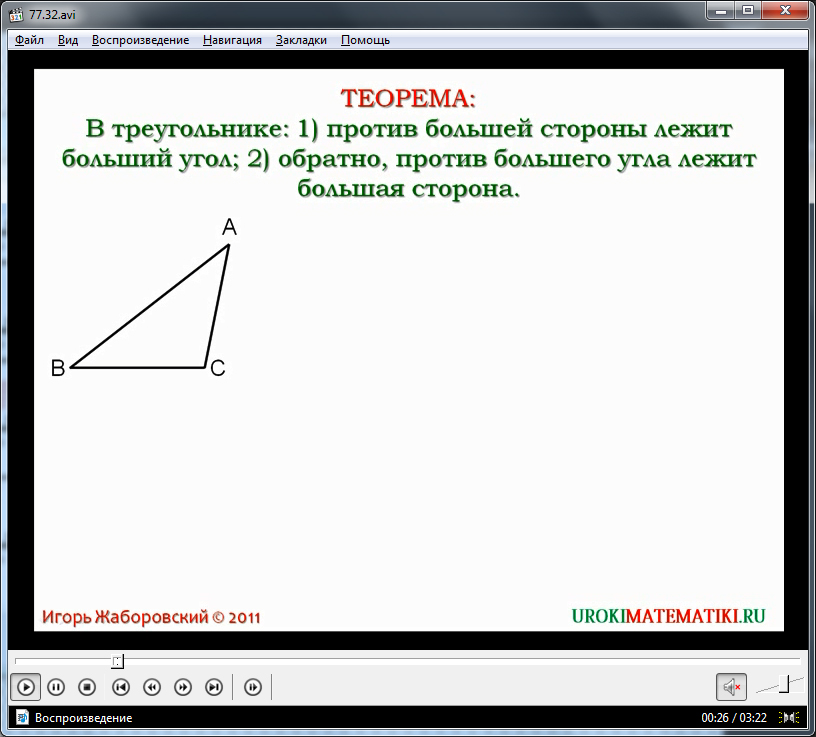
В начале видеоурока после представления темы на экран выводится текст теоремы, которая утверждает о том, что против большей стороны в произвольном треугольнике располагается больший угол, н напротив большего угла всегда расположена большая сторона. Данное утверждение демонстрируется на треугольнике ΔАВС, который отображается на рисунке ниже текста теоремы. Доказательство теоремы объясняется устно диктором.
Для доказательства утверждения предполагается рассмотреть стороны AB, AC и углы, расположенные напротив них - ∠C и ∠B. Предполагается, что для сторон AB>AC напротив лежащие углы будут ∠C>∠B. На стороне AB откладывается отрезок AD, равный по величине отрезку AC. Так как сторона AC меньше стороны AB, то конец отрезка точка D лежит между вершинами треугольника A и B. Из этого следует, что образовавший при построении угол ∠1 меньше угла ∠C, а угол ∠2 как внешний к углу ∠BDC равняется сумме углов ∠DBC и ∠DCB. Это означает, что ∠2 больше угла ∠DBC=∠B. Соответственно, и угол ∠C больше угла ∠B.
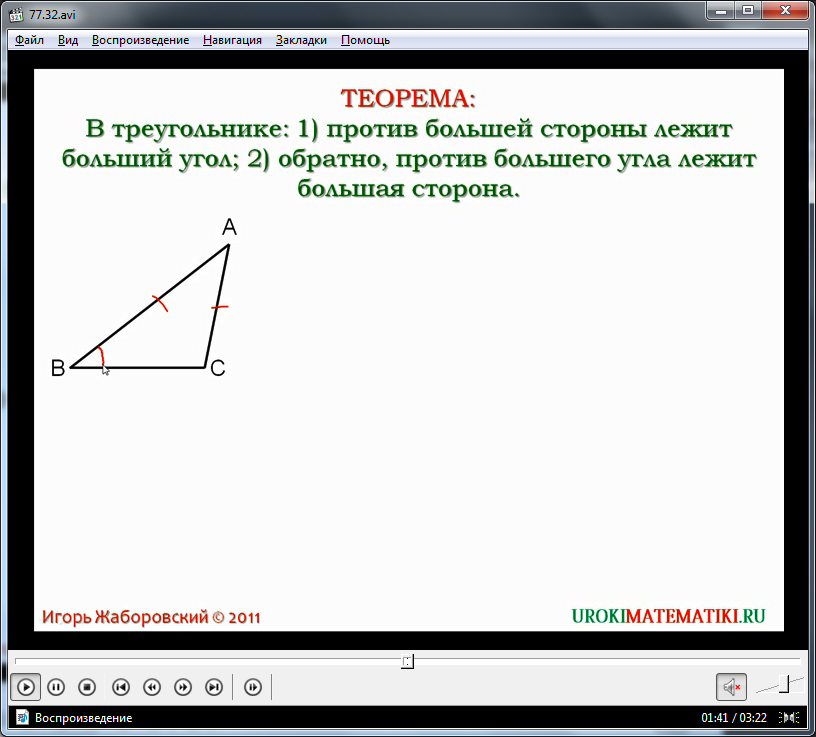
Доказательство обратного утверждения сводится к рассмотрению соотношения сторон AB, AC, если угол ∠C больше угла ∠B. Выполняется доказательство от противного. Для этого предполагается, что при ∠C>∠B сторона AB равна или меньше стороны AC. Однако с учетов равенства сторон AB=AC, зная свойства равнобедренного треугольника, можно утверждать, что в этом случае углы ∠C=∠B также будут равны. Если же AB<AC, то с учетом первой части теоремы о соотношениях сторон и углов, можно утверждать, что ∠C<∠B. Оба результата оказались неверными, так как противоречат условию. Значит, утверждение верно, и AB>AC.
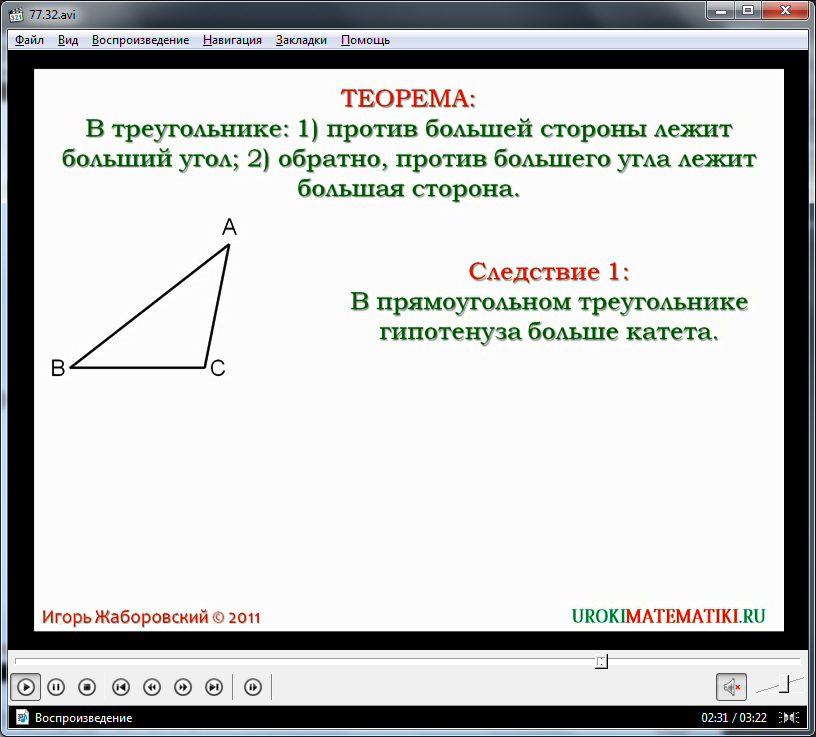
Далее в видеоуроке рассматриваются следствия данной теоремы. Утверждается, что исходя из данной теоремы гипотенуза прямоугольного треугольника всегда больше катета. Действительно, так как гипотенуза лежит напротив прямого угла, то катеты располагаются напротив острых углов. Так как острые углы всегда меньше прямого, то и противолежащие стороны-катеты всегда меньше гипотенузы.
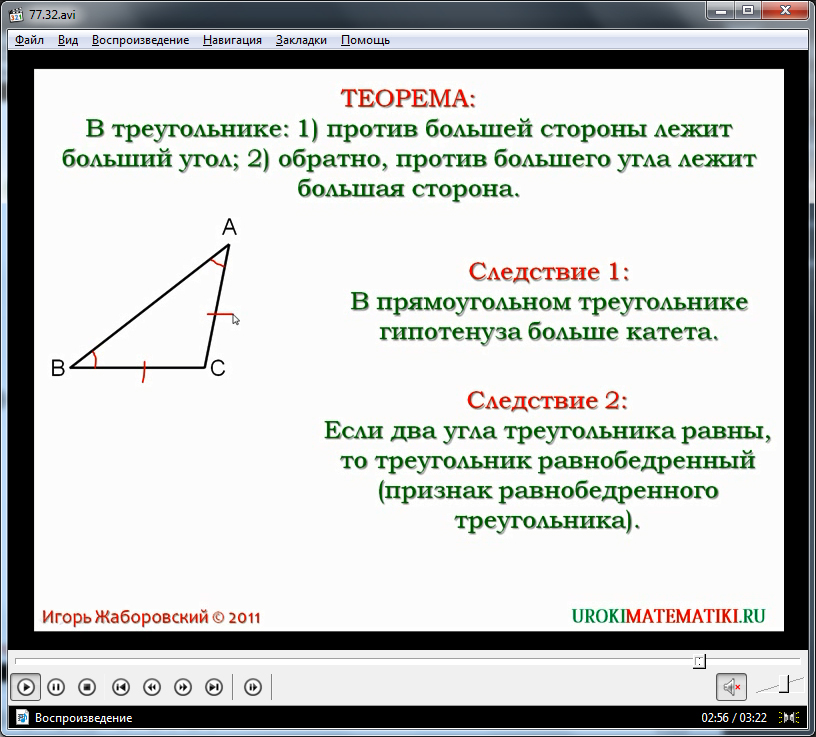
Второе следствие теоремы – признак равнобедренного треугольника. Данное следствие утверждает, что равенство двух углов треугольника означает, что он равнобедренный. На примере треугольника ΔABC рассматриваются два угла ∠C и ∠B, и противолежащие им стороны AB и AC. Предполагается, что равенству углов ∠C=∠B соответствует равенство сторон AB=AC. Действительно, если бы стороны не были равны, то по теореме напротив большей стороны лежал бы больший угол, а напротив меньшей стороны лежал бы меньший угол. Таким образом, предположение о неравенстве сторон неверно. Данный треугольник является равнобедренным. Следствие доказано.
| Автор | |
|---|---|
| Дата добавления | 02.08.2014 |
| Раздел | Геометрия |
| Подраздел | Видеоурок |
| Просмотров | 7412 |
| Номер материала | 519 |