
Презентация по математике Мячиной В. (10 "Б" класс) на тему " Задачки из ЕГЭ №20"





























Описание презентации по отдельным слайдам:
Задание: Экзамен включает 30 заданий. За каждое верно выполненное задание ученик получает 3 балла, за неверный ответ снимают 2 балла, задание без ответа не приносит баллы и не отнимает их. Какое максимальное количество ошибок мог допустить ученик, если в итоге он получил 44 балла? Решение: Пусть x заданий решено верно, y — с ошибкой и n — не решено вообще. Тогда всего задач x+y+n=30, и получено баллов 3x+2y=44. Подставив x=30-n-y во второе уравнение получим: 5y=46-3n. Выбираем значение n таким, чтобы количество ошибок было максимально и y осталось целым числом, т.е. n=2. 5y=46-3⋅2=40. y=8 — максимальное количество ошибок с результатом 44 балла Ответ: 8
Задание: Улитка за день залезает вверх по дереву на 2 м, а за ночь сползает на 1 м. Высота дерева 9 м. За сколько дней улитка доползет до вершины дерева? Ответ: 8 Решение: Заметим, что в этой задаче следует различать понятие "сутки" и понятие "день". В задаче спрашивается именно за сколько дней улитка доползет до вершины дерева. За один день улитка поднимается на 2 м, а за одни сутки улитка поднимается на 1 м (за день поднимается на 2 м, а потом за ночь спускается на 1 м). За 7 суток улитка поднимается на 7 метров. То есть утром 8-го дня ей останется доползти до вершины 2 м. И за восьмой день она преодолеет это расстояние.
Задание: В корзине лежат 30 грибов: рыжики и грузди. Известно, что среди любых 12 грибов имеется хотя бы один рыжик, а среди любых 20 грибов хотя бы один груздь. Сколько рыжиков в корзине? Решение: Так как среди любых 12 грибов имеется хотя бы один рыжик (или больше) число груздей должно быть меньше или равно чем 12-1=11 Отсюда следует, что число рыжиков больше или равно чем 30-11=19 Так как среди любых 20 грибов хотя бы один груздь (или больше), число рыжиков должно быть меньше или равно чем 20-1=19 Тогда получили, что с одной стороны, число рыжиков больше или равно чем 19, а с другой - меньше или равно чем 19. Следовательно, число рыжиков равно 19. Ответ: 19
3адание: Саша пригласил Петю в гости, сказав, что живёт в седьмом подъезде в квартире № 333, а этаж сказать забыл. Подойдя к дому, Петя обнаружил, что дом девятиэтажный. На каком этаже живёт Саша? (На каждом этаже число квартир одинаково, номера квартир в доме начинаются с единицы.) Ответ: 2
Задание: Список заданий викторины состоял из 25 вопросов. За каждый правильный ответ ученик получал 7 очков, за неправильный ответ с него списывали 9 очков, а при отсутствии ответа давали 0 очков. Сколько верных ответов дал ученик, набравший 56 очков, если известно, что по крайней мере один раз он ошибся? Ответ: 17
Задание: Из книги выпало несколько идущих подряд листов. Номер последней страницы перед выпавшими листами — 352, номер первой страницы после выпавших листов записывается теми же цифрами, но в другом порядке. Сколько листов выпало? Ответ: 85
Задание: Десять столбов соединены между собой проводами так, что от каждого столба отходит ровно 8 проводов. сколько всего проводов протянуто между этими десятью столбами? Ответ: 40
Задание: В конце четверти Петя выписал подряд все свои отметки по одному из предметов, их оказалось 5, и поставил между некоторыми из них знаки умножения . Произведение получившихся чисел оказалось равным 3495 . Какая отметка выходит у Пети в четверти по этому предмету, если учитель ставит только отметки 2, 3, 4 или 5 и итоговая отметка в четверти является средним арифметическим всех текущих отметок, округленным по правилам округления? (Например, 3,2 округляется до 3; 4,5 - до 5; 2,8 - до 3) Ответ: 3
Задание: Среднее арифметическое 6 различных натуральных чисел равно 8. На сколько нужно увеличить наибольшее из этих чисел, чтобы их среднее арифметическое стало на 1 больше? Ответ: 6
Задание: Прямоугольник разбит на четыре маленьких прямоугольника двумя прямолинейными разрезами. Площади трех из них, начиная с левого верхнего и далее по часовой стрелке равны 15, 18, 24. Найдите площадь четвертого прямоугольника. Ответ: 20
Задание: На поверхности глобуса фломастером проведены 17 параллелей и 24 меридиана. На сколько частей проведённые линии разделяют поверхность глобуса? Меридиан – это дуга окружности, соединяющая Северный и Южный полюса. параллель – это окружность, лежащая в плоскости, параллельной плоскости экватора. Ответ: 432
Задание: Хозяин договорился с рабочими, что они копают колодец на следующих условиях: за первый метр он заплатит им 3500 рублей, а за каждый следующий метр – на 1600 рублей больше, чем за предыдущий. Сколько денег хозяин должен будет заплатить рабочим, если они выкопают колодец глубиной 9 метров? Ответ: 89100
Задание: Маша и Медведь съели 100 печений и банку варенья, начав и закончив одновременно. Сначала Маша ела варенье, а Медведь — печенья, но в какой-то момент они поменялись. Медведь и то, и другое ест в три раза быстрее Маши. Сколько печений съел Медведь, если варенья они съели поровну? Ответ: 90
Задание: На палке отмечены поперечные линии красного, жёлтого и зелёного цвета. Если распилить палку по красным линиям, получится 5 кусков, если по жёлтым – 7 кусков, а если по зелёным – 11 кусков. Сколько кусков получится, если распилить палку по линиям всех трёх цветов? Ответ: 21
Задание : На прилавке цветочного магазина стоят 3 вазы с розами: оранжевая, белая и синяя. Слева от оранжевой вазы 15 роз, справа от синей вазы 12 роз. Всего в вазах 22 розы. сколько роз в оранжевой вазе? Ответ: 7
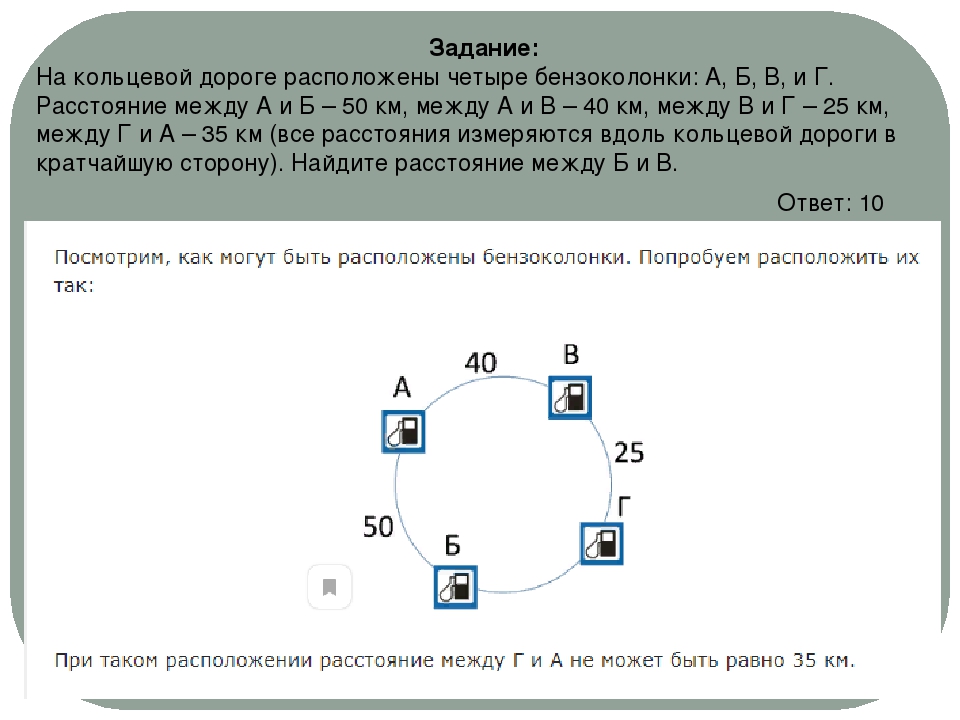
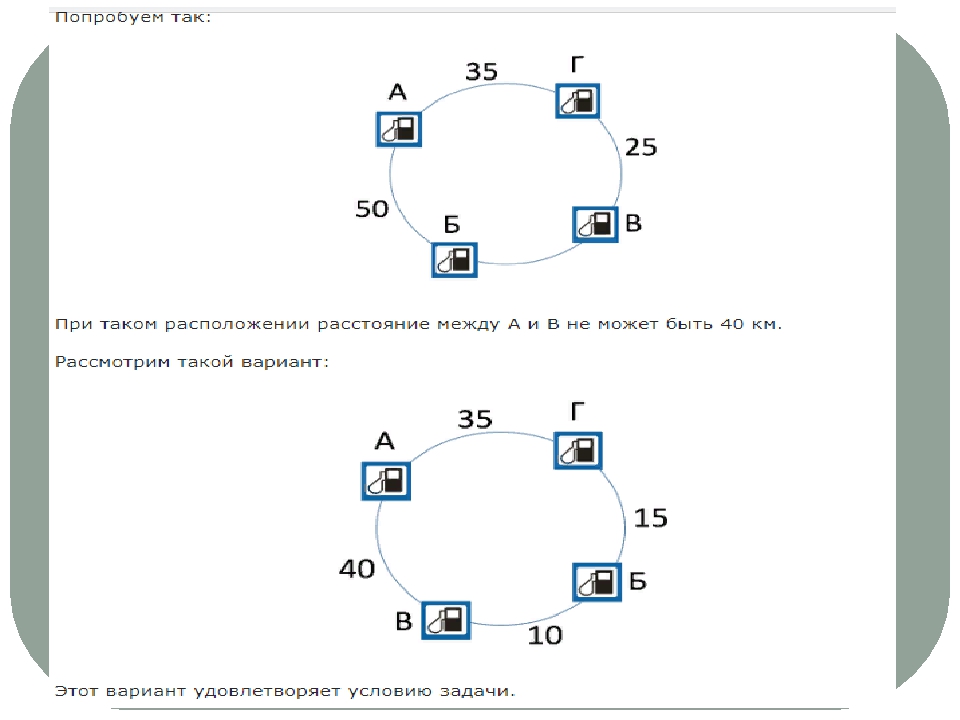
Задание: На кольцевой дороге расположены четыре бензоколонки: A, Б, B, и Г. Расстояние между A и Б – 50 км, между A и В – 40 км, между В и Г – 25 км, между Г и A – 35 км (все расстояния измеряются вдоль кольцевой дороги в кратчайшую сторону). Найдите расстояние между Б и В. Ответ: 10
Задание: Во всех подъездах дома одинаковое число этажей, а на каждом этаже одинаковое число квартир. При этом число этажей в доме больше числа квартир на этаже, число квартир на этаже больше числа подъездов, а число подъездов больше одного. Сколько этажей в доме, если всего в нём 105 квартир? Ответ: 7
Задание: В таблице три столбца и несколько строк. В каждую клетку таблицы поставили по натуральному числу так, что сумма всех чисел в первом столбце равна 72, во втором – 81, в третьем – 91, а сумма чисел в каждой строке больше 13, но меньше 16. Сколько всего строк в таблице? Ответ:17
Задание: Три луча, выходящие из одной точки, разбивают плоскость на три разных угла, измеряемых целым числом градусов. Наибольший угол в 3 раза больше наименьшего. Сколько значений может принимать величина среднего угла? Ответ: 20
В обменном пункте можно совершить одну из двух операций: за 2 золотые монеты получить 3 серебряные и одну медную за 5 серебряных монет получить 3 золотые и одну медную. У Николая были только серебряные монеты. После нескольких посещений обменного пункта серебряных монет у него стало меньше, золотых не появилось, зато появилось 5050 медных. На сколько уменьшилось количество серебряных монет у Николая? Ответ: 10
Сколькими способами можно выложить в ряд три одинаковых красных шарика, два одинаковых зелёных шарика и один синий шарик? Ответ: 60
Альпинист поднимается на гору высотой 300300 метров. Первые 5050 метров он преодолевает за 1010 минут, каждые следующие 5050 метров — на 22 минуты дольше, чем предыдущие. После отдыха на вершине в течение 3030 минут альпинист начинает спуск с равномерной скоростью 55 минут на каждые 5050 метров. Через сколько часов альпинист снова окажется у подножия горы?
В лотке 30 яиц: белые и рябые. Известно, что среди любых 12яиц имеется хотя бы одно рябое, а среди любых 20 яиц хотя бы одно белое. Сколько белых яиц в лотке? Ответ: 11 Так как среди любых 12 яиц имеется хотя бы одно рябое, то белых яиц не может быть больше 11. А поскольку среди любых 20 яиц хотя бы одно белое, то рябых яиц не может быть больше 19. Так как всего в лотке 30 яиц, то единственный возможный вариант — в лотке 19 рябых яиц и 11 белых.

| Автор | |
|---|---|
| Дата добавления | 03.06.2019 |
| Раздел | Алгебра |
| Подраздел | Презентация |
| Просмотров | 1980 |
| Номер материала | 6252 |