Презентация по математике Соколовой Е. (11 "Б" класс) на тему " Корень п-й степени"

Корень n-ой степени Выполнила: ученица 11 класса «Б» Соколова Елена Александровна

Понятие корня n-ой степени Корнем n-ой степени из неотрицательного числа а (n = 2, 3, 4, 5, ...) называют такое неотрицательное число, при возведении которого в степень п получается число а. Число а называют подкоренным числом, а число n – показателем корня

Примеры

Свойства корня n-ой степени (для n ∈ N, k ∈ N, n > 1, k > 1)

Свойства корня n-ой степени (для n ∈ N, k ∈ N, n > 1, k > 1)

Свойства корня n-ой степени (для n ∈ N, k ∈ N, n > 1, k > 1)

Свойства корня n-ой степени (для n ∈ N, k ∈ N, n > 1, k > 1)

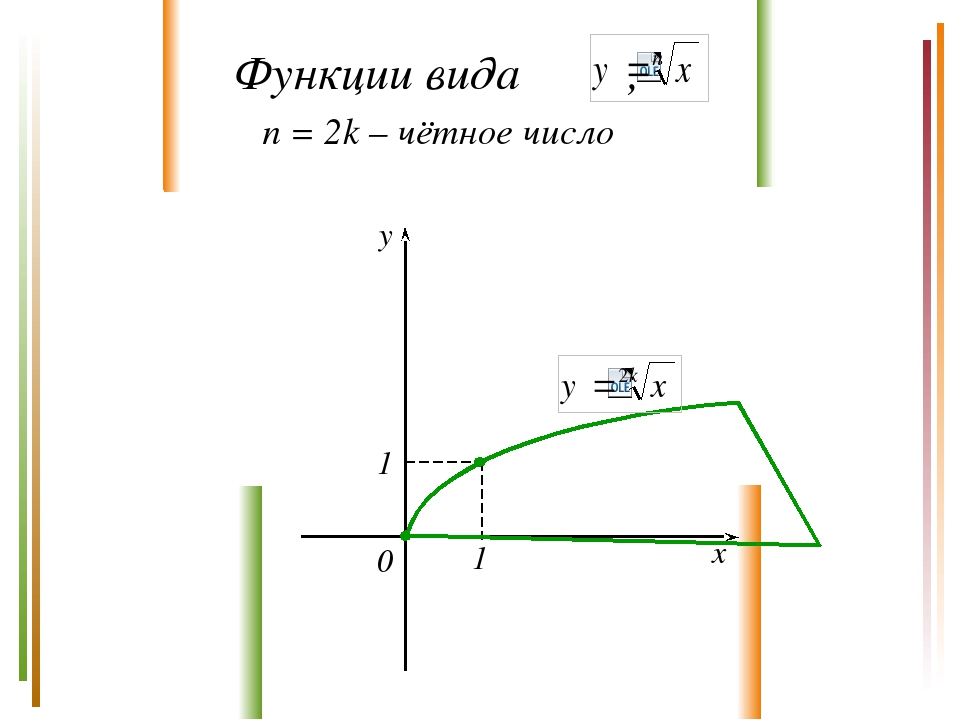
Свойства функции , n – чётное число D(у) = [0; +). E(у) = [0; +). Функция ни чётная, ни нечётная. а) Нули функции: (0; 0). б) Точка пересечения с Оу: (0; 0). [0; +) – промежуток возрастания функции; Ограничена снизу, не ограничена сверху. а) унаим. = 0; б) унаиб. – не существует. Непрерывна на множестве [0; +). Выпукла вверх. Функции вида

y x 0 1 1 n = 2k – чётное число Функции вида ,

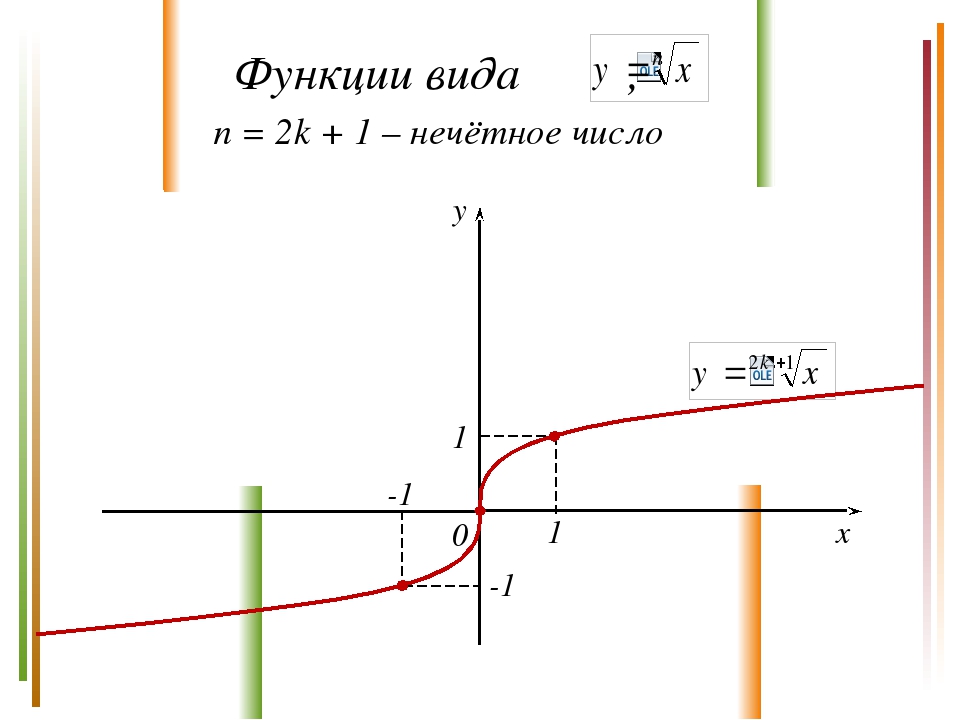
Свойства функции , n – нечётное число D(у) = (-; +). E(у) = (-; +). Функция нечётная. а) Нули функции: (0; 0). б) Точка пересечения с Оу: (0; 0). (-; +) – промежуток возрастания функции; Не ограничена снизу, не ограничена сверху. а) унаим. – не существует; б) унаиб. – не существует. Непрерывна на множестве (-; +). Функции вида

y x 0 1 1 -1 -1 n = 2k + 1 – нечётное число Функции вида ,

Вычисление производной

Вычисление производной Примеры

Формула сложного радикала Примеры

МБОУ СОШ №5 – «Школа здоровья и развития» г. Радужный Степень с рациональным показателем Учитель математики Е.Ю. Семёнова

Понятие степени с рациональным показателем Примеры

Свойства степени с рациональным показателем (для n ∈ Q, k ∈ Q)

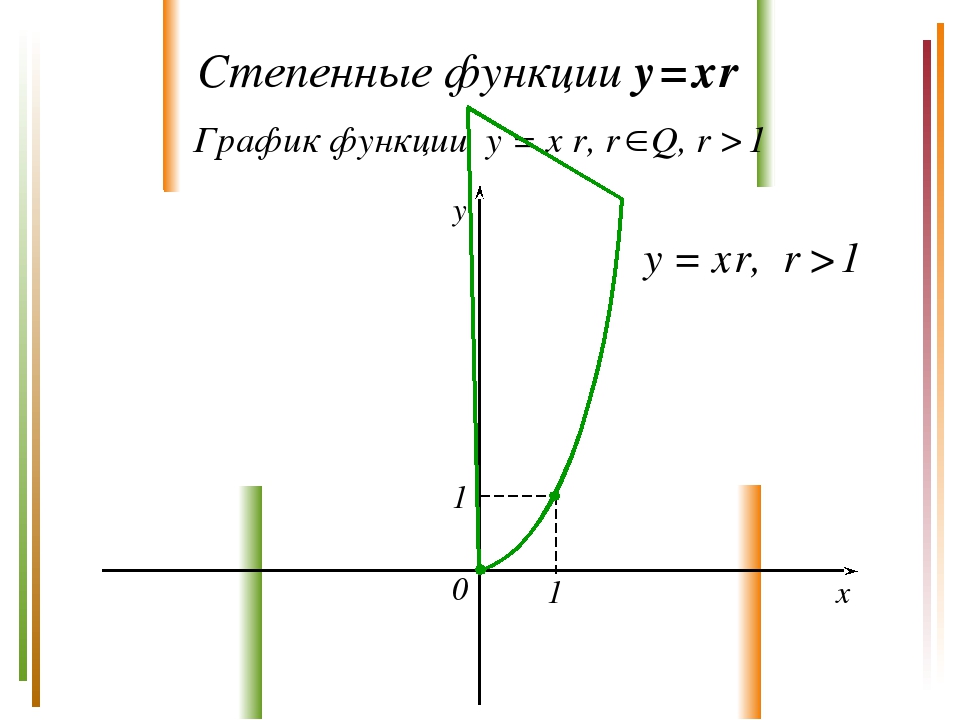
Степенные функции y = x r Свойства функции y = x r, r Q, r > 1 D(у) = [0; +). E(у) = [0; +). Функция ни четная, ни нечетная. а) Нули функции: (0; 0). б) Точка пересечения с Оу: (0; 0). [0; +) – промежуток возрастания функции; Ограничена снизу, не ограничена сверху. а) унаим. = 0; б) унаиб. – не существует. Непрерывна на множестве [0; +). Выпукла вниз.

Степенные функции y = x r График функции y = x r, r Q, r > 1 y x 0 y = x r, r > 1 1 1

Степенные функции y = x r Свойства функции y = x r, r Q, 0 < r < 1 D(у) = [0; +). E(у) = [0; +). Функция ни четная, ни нечетная. а) Нули функции: (0; 0). б) Точка пересечения с Оу: (0; 0). [0; +) – промежуток возрастания функции; Ограничена снизу, не ограничена сверху. а) унаим. = 0; б) унаиб. – не существует. Непрерывна на множестве [0; +). Выпукла вверх.

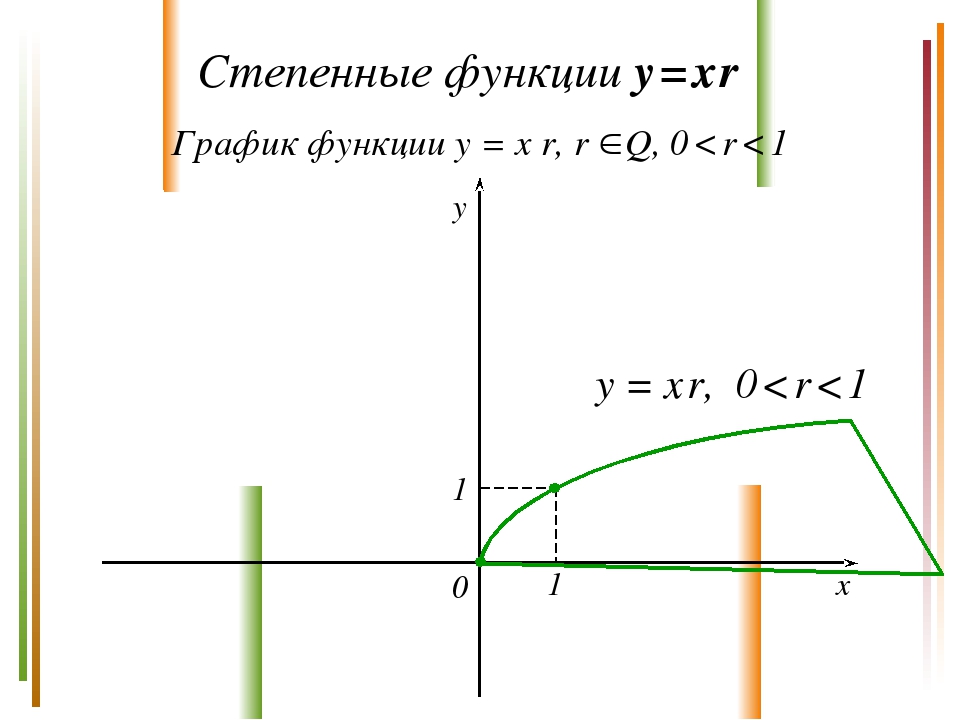
Степенные функции y = x r График функции y = x r, r Q, 0 < r < 1 y x 0 y = x r, 0 < r < 1 1 1

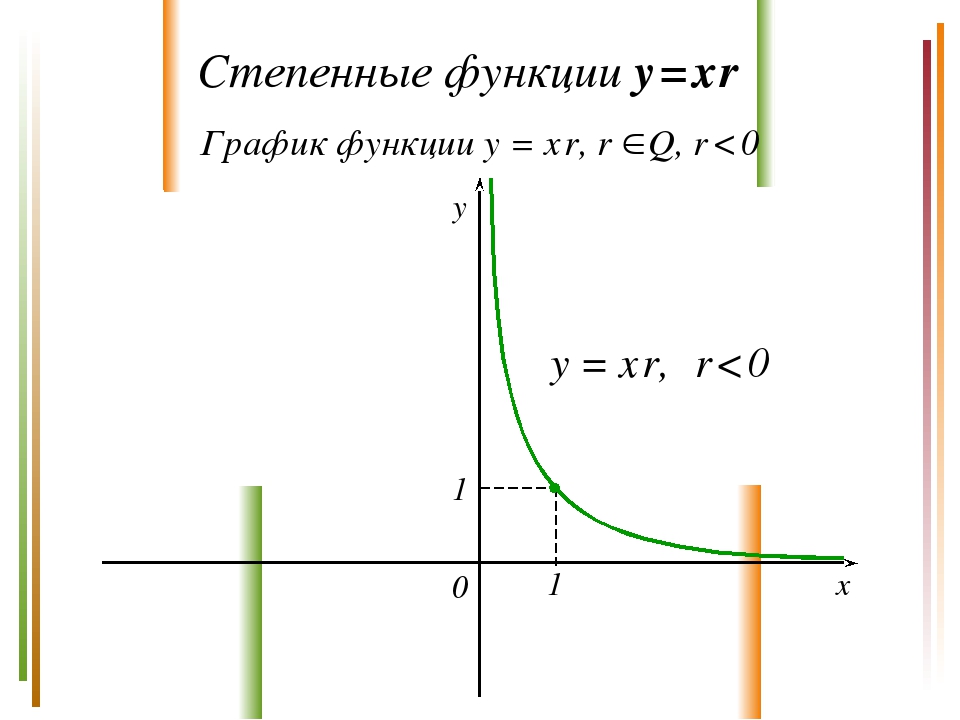
Степенные функции y = x r Свойства функции y = x r, r Q, r < 0 D(у) = (0; +). E(у) = (0; +). Функция ни четная, ни нечетная. а) Нули функции: нет. б) Точка пересечения с Оу: нет. (0; +) – промежуток убывания функции; Ограничена снизу, не ограничена сверху. а) унаим. – не существует; б) унаиб. – не существует. Непрерывна на множестве [0; +). Выпукла вниз.

Степенные функции y = x r График функции y = x r, r Q, r < 0 y x 0 y = x r, r < 0 1 1

Задания открытого банка задач Решение. Решение. Решение. 1. Найдите значение выражения . 2. Найдите значение выражения . 3. Найдите значение выражения .

Задания открытого банка задач Решение. Решение. Решение. 4. Найдите значение выражения . 5. Найдите значение выражения . 6. Найдите значение выражения .

Задания открытого банка задач Решение. Решение. Решение. 7. Найдите значение выражения . 8. Найдите значение выражения . 9. Найдите значение выражения .

Задания открытого банка задач Решение. Решение. 10. Найдите значение выражения . 11. Найдите значение выражения .

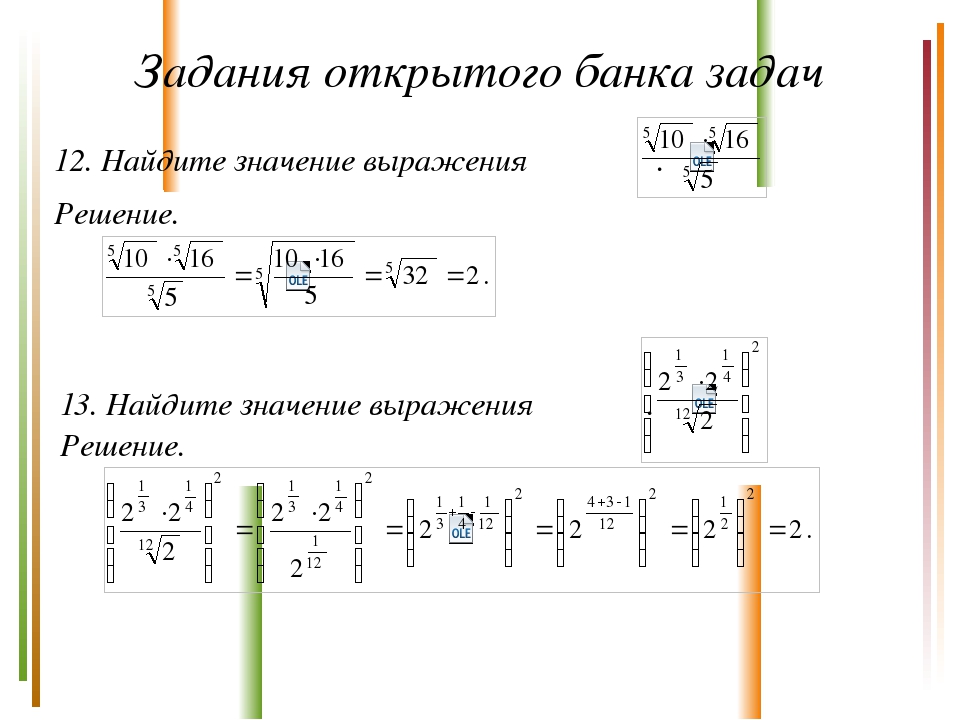
Задания открытого банка задач Решение. Решение. 12. Найдите значение выражения . 13. Найдите значение выражения .

Спасибо за внимание!!!!