
Презентация " Правильные многогранники"









Описание презентации по отдельным слайдам:
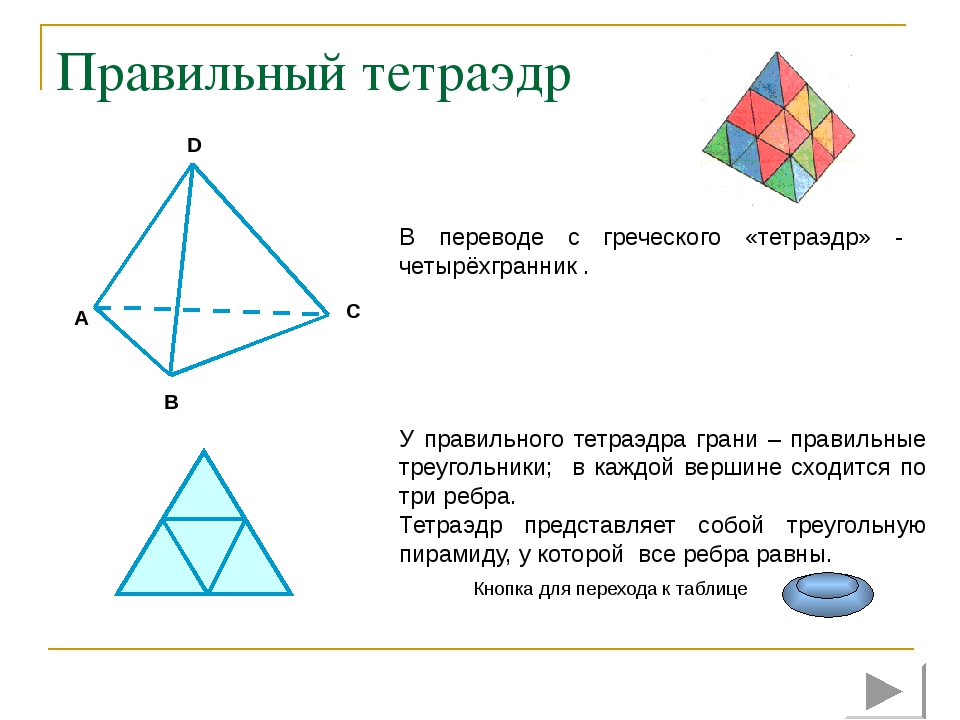
Правильный тетраэдр C В переводе с греческого «тетраэдр» - четырёхгранник . У правильного тетраэдра грани – правильные треугольники; в каждой вершине сходится по три ребра. Тетраэдр представляет собой треугольную пирамиду, у которой все ребра равны. Кнопка для перехода к таблице A B D
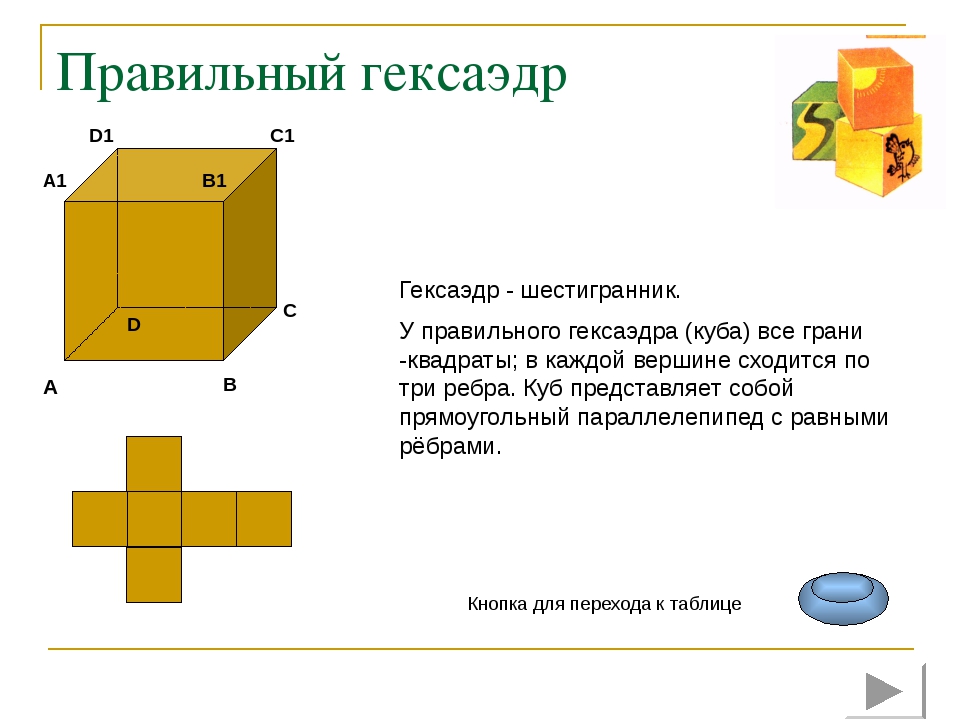
Правильный гексаэдр Гексаэдр - шестигранник. У правильного гексаэдра (куба) все грани -квадраты; в каждой вершине сходится по три ребра. Куб представляет собой прямоугольный параллелепипед с равными рёбрами. Кнопка для перехода к таблице А B C1 D1 C D B1 A1
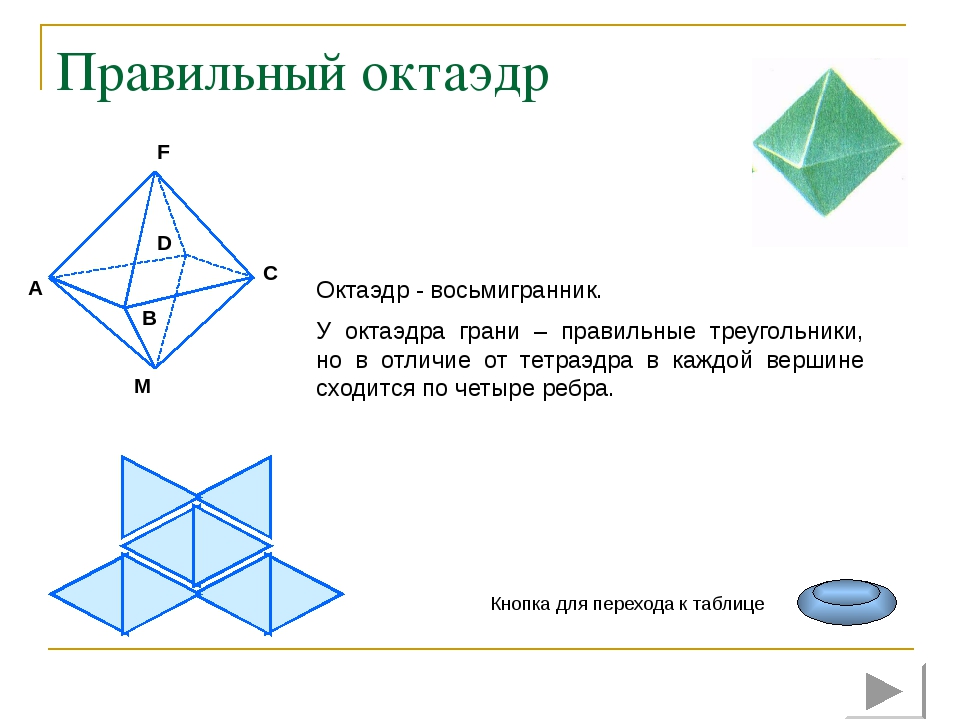
Правильный октаэдр Октаэдр - восьмигранник. У октаэдра грани – правильные треугольники, но в отличие от тетраэдра в каждой вершине сходится по четыре ребра. Кнопка для перехода к таблице A M C B F D
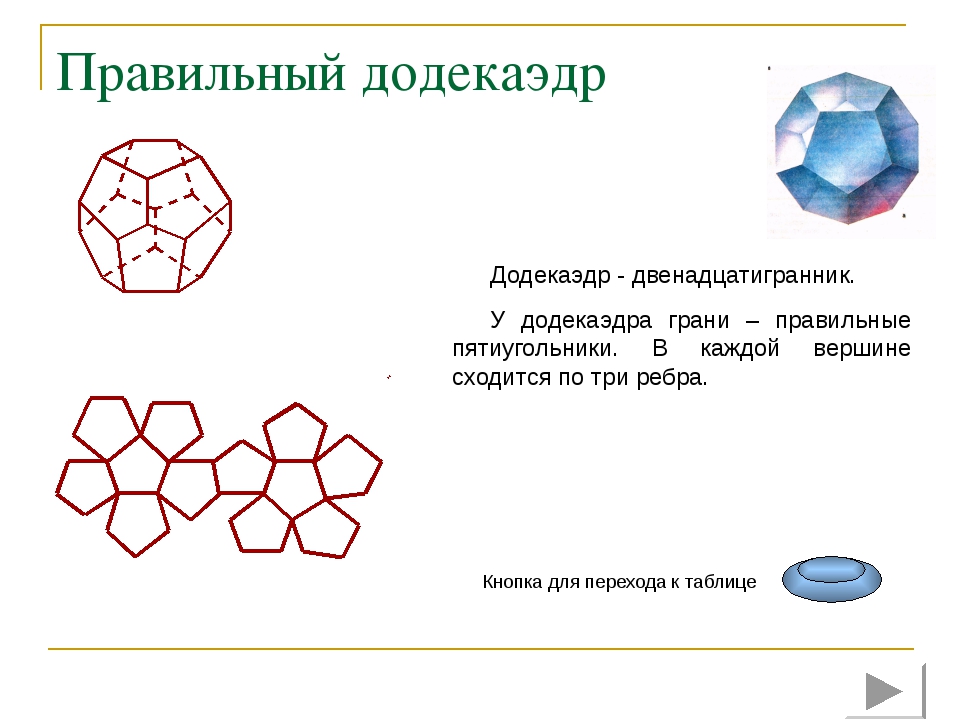
Правильный додекаэдр Додекаэдр - двенадцатигранник. У додекаэдра грани – правильные пятиугольники. В каждой вершине сходится по три ребра. Кнопка для перехода к таблице
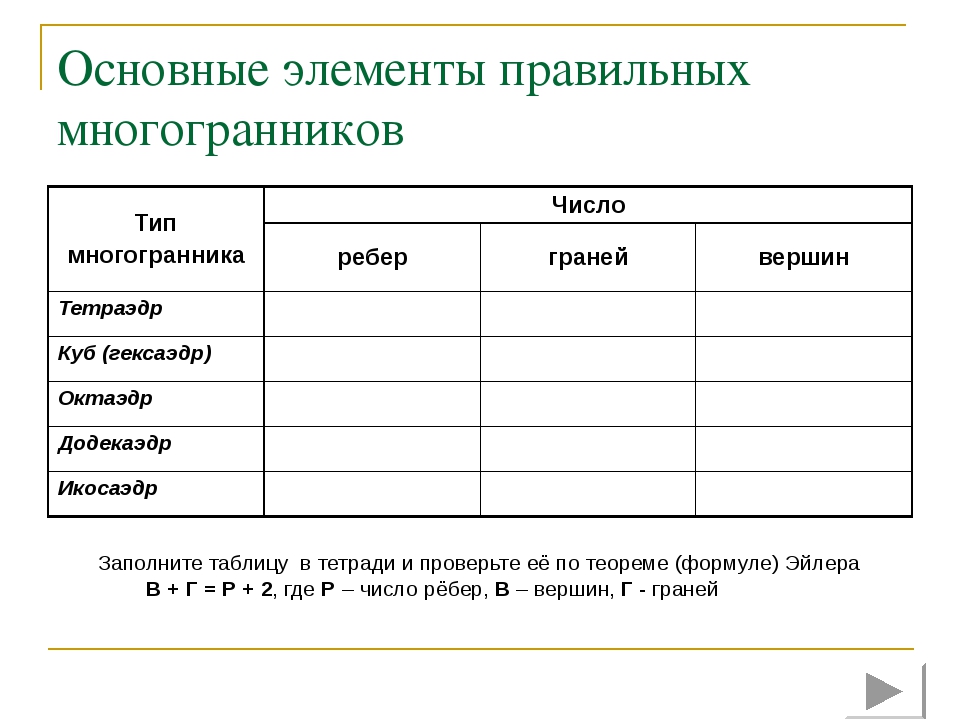
Леонард Эйлер (1707-1783г.г.) Эйлер - швейцарский математик и механик, академик Петербургской Академии Наук, автор огромного количества глубоких результатов во всех областях математики. Полное собрание сочинений Эйлера-72 тома-не вышло целиком и до сих пор. По единодушному признанию современников Леонард Эйлер - первый математик мира. В геометрии Эйлер положил начало совершенно новой области исследований, выросшей впоследствии в самостоятельную науку — топологию. Имя Эйлера носит формула, связывающая число вершин (В), ребер (Р) и граней (Г) выпуклого многогранника: В + Г = Р + 2 «Эйлер не проглядел ничего в современной ему математике, хотя последние семнадцать лет своей жизни был совершенно слеп». Э.Т.Белл
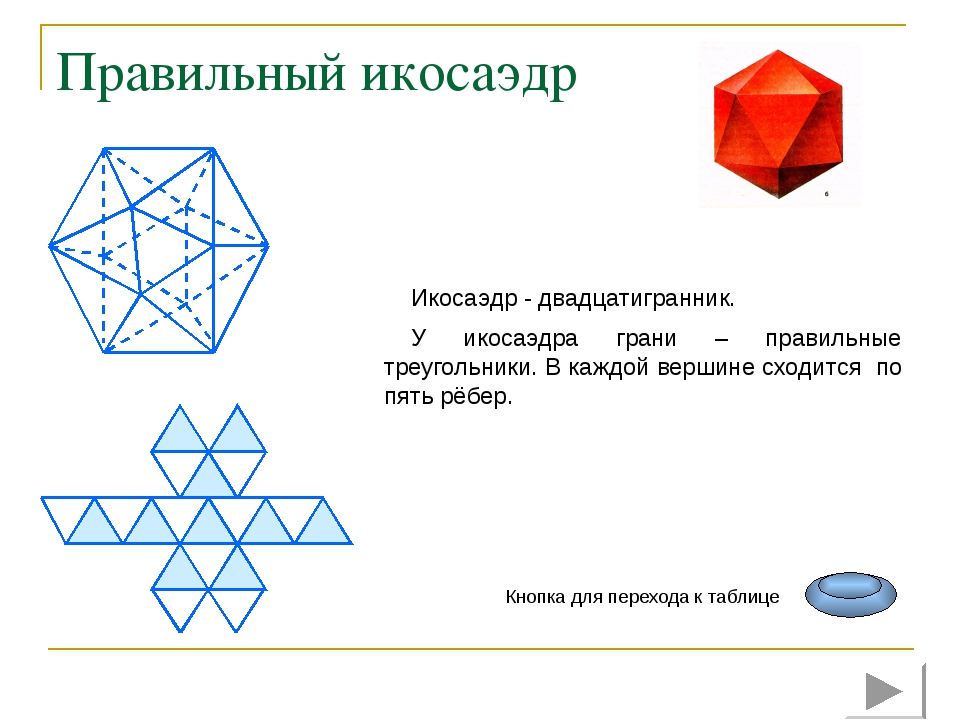
Правильный икосаэдр Икосаэдр - двадцатигранник. У икосаэдра грани – правильные треугольники. В каждой вершине сходится по пять рёбер. Кнопка для перехода к таблице
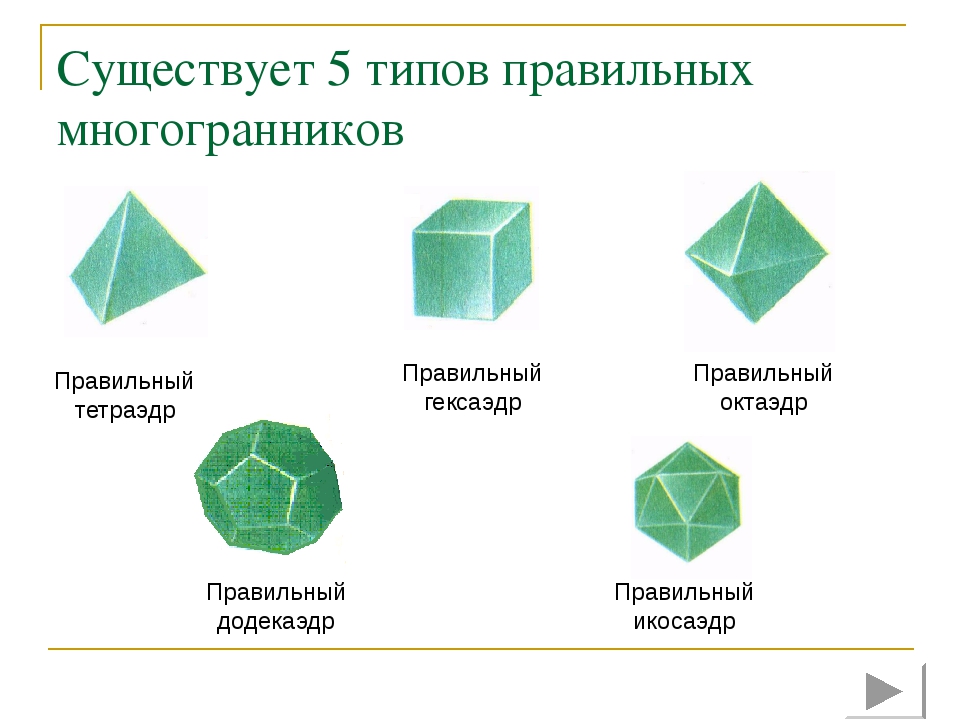
Историческая справка О существовании всего лишь пяти правильных многогранников знали еще в Древней Греции. Великий древнегреческий мыслитель Платон считал, что четыре из них олицетворяют четыре «стихии»: тетраэдр – огонь, куб – землю, икосаэдр – воду, октаэдр – воздух. Пятый же многогранник, додекаэдр, символизировал собой все мироздание, представлял собой образ всей Вселенной, почитался главнейшим и его стали называть quinta essentia (квинта эссенциа») или «пятая сущность». Правильные многогранники называют иногда Платоновыми телами, им посвящена последняя книга «Начал» Евклида. Её считают венцом стереометрии у древних греков.
Леонард Эйлер (1707-1783г.г.) Эйлер - швейцарский математик и механик, академик Петербургской Академии Наук, автор огромного количества глубоких результатов во всех областях математики. Полное собрание сочинений Эйлера-72 тома-не вышло целиком и до сих пор. По единодушному признанию современников Леонард Эйлер - первый математик мира. В геометрии Эйлер положил начало совершенно новой области исследований, выросшей впоследствии в самостоятельную науку — топологию. Имя Эйлера носит формула, связывающая число вершин (В), ребер (Р) и граней (Г) выпуклого многогранника: В + Г = Р + 2 «Эйлер не проглядел ничего в современной ему математике, хотя последние семнадцать лет своей жизни был совершенно слеп». Э.Т.Белл
Применение в кристаллографии Тела Платона нашли широкое применение в кристаллографии, так как многие кристаллы имеют форму правильных многогранников. Например, куб - монокристалл поваренной соли (NaCl), октаэдр - монокристалл алюмокалиевых квасцов, одна из форм кристаллов алмаза - октаэдр Кристаллы бывают самой различной формы: 1 — берилл, 2 — аметист, 3 — рубин, 4 — кристалл металла германия — денорит, 5 — горный хрусталь, 6 — испанский шпат, 7 — поваренная соль, 8 — ограненный алмаз—бриллиант, вправленный в кольцо. В колбе с перенасыщенным раствором на конце проволочки, опущенной в раствор, растет кристалл поваренной соли.
Поваренная соль состоит из кристаллов в форме куба Скелет одноклеточного организма феодарии представляет собой икосаэдр. Минерал сильвин также имеет кристаллическую решетку в форме куба. Молекулы воды имеют форму тетраэдра. Минерал куприт образует кристаллы в форме октаэдров. Кристаллы пирита имеют форму додекаэдра

| Автор | |
|---|---|
| Дата добавления | 19.12.2018 |
| Раздел | Геометрия |
| Подраздел | Презентация |
| Просмотров | 2115 |
| Номер материала | 5993 |