
Презентация "Треугольник"

Краткое описание документа:
На этом уроке пройдёт первое знакомство с важнейшей фигурой в геометрии, а именно: треугольником. Одной из центральных теорем в геометрии является теорема о сумме углов треугольника. Именно она определяет их виды: остроугольные, тупоугольные, прямоугольные. Теорема звучит следующим образом: сумма углов треугольника равна ста восьмидесяти градусам. Действительно, теорема удивительная! Сколько на свете треугольников? Их бесчисленное множество, а сумма углов всегда будет одна.

слайды 1-2 (Тема презентации "Треугольник", пример)
В принципе и доказательство того, что сумма всех углов в треугольнике равно ста восьмидесяти, - это действие несложное. Для того чтобы доказать это, необходимо сделать дополнительное построение. Через точку «В» проведём прямую, которая будет параллельна стороне «АС». Такая прямая существует и единственная. Тогда получаем, что, по свойству параллельных прямых, оставшиеся углы при «А» и «С» будут равны углам при точке «В» с прямой. А в сумме при точке «А» по одной стороне прямой будет сто восемьдесят градусов.
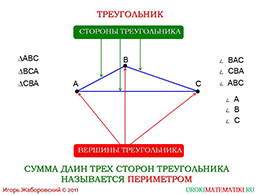
Теперь стоит остановиться на основных элементах, которые характерны треугольнику. Возьмём три точки: «А», «В», «С», не лежащие на одной прямой, то есть точка «С» не лежит на прямой «АВ». Соединяем все эти точки отрезками. Когда мы произвели это действие, то получили необходимую нам фигуру – треугольник «АВС». Кто может сказать, какой это треугольник: остроугольный, тупоугольный или прямоугольный? Точки выступают вершинами треугольника, а отрезки «АВ», «ВС», «СА» – его сторонами, также треугольник имеет три угла «А», «В» и «С», которые более подробно называют углами «ВАС», «СВА» и «АВС». Называть треугольник мы также можем тремя способами: АВС, ВАС и СВА.
Далее необходимо остановится на определении «периметр треугольника». Периметром треугольника называется сумма длин всех его сторон. В нашем случае периметром является сумма отрезков «АВ», «ВС» и «АС», а сам периметр обозначаем буквой «Р».
слайды 3-4 (примеры)
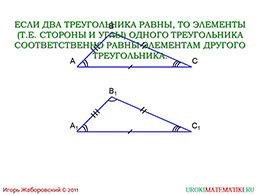
Две фигуры являются равными, если их можно совместить наложением. Это же определение и относится к треугольникам. Получается, что треугольник «АВС» равен треугольнику «А1В1С1», если эти треугольники можно совместить наложением, при этом совместятся вершины «А» и «А1», «В» и «В1», «С» и «С1»; совместятся стороны «АВ» и «А1В1», «ВС» и «В1С1», «АС» и «А1С1»; а также совместятся углы «А» и «А1», «В» и «В1», «С» и «С1». Однако как мы можем осуществить это наложение во время урока? Есть несколько способов для того, чтобы произвести данный процесс: мы можем вырезать ножницами эти два треугольника и приложить. Однако тогда мы повредим тетрадь или учебник. Второй вариант – визуально «на глаз» посмотреть и понять, что они идентичны. Хороший вариант, менее травмирующий, но может иметь погрешность, причём большую. Что остаётся в таком случае? Необходимы более измеряемые параметры, которые помогут сделать все просчёты, поэтому обратимся ко второму способу анализа фигур.
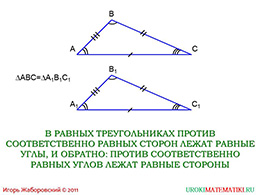
У треугольника много элементов, но в равных треугольниках совместившиеся элементы равны. Что означает, когда треугольник «АВС» равен треугольнику «А1В1С1»? Это означает, что сторона «АВ» идентичная стороне «А1В1», более того они лежат против равных углов «А» и «А1». Что по поводу остальных сторон? Они тоже будут равны. Углы также равны относительно друг друга. Мы видим, что против равных углов находятся равные стороны и, наоборот, против равных сторон лежат равные углы.
Подытожим информацию о том, как доказать равенство треугольников? Есть два способа, где в первом надо сравнить все элементы одновременно, то есть совместить их, если удастся. Способ вроде бы и несложный, но трудоёмкий. По второму способу необходимо сравнить часть элементов, но с гарантией совмещения всех остальных элементов. То есть во втором случае необходимо разработать признаки равенства треугольников.
| Автор | |
|---|---|
| Дата добавления | 02.08.2014 |
| Раздел | Геометрия |
| Подраздел | Презентация |
| Просмотров | 3837 |
| Номер материала | 239 |