Признак перпендикулярности прямой и плоскости













Описание презентации по отдельным слайдам:
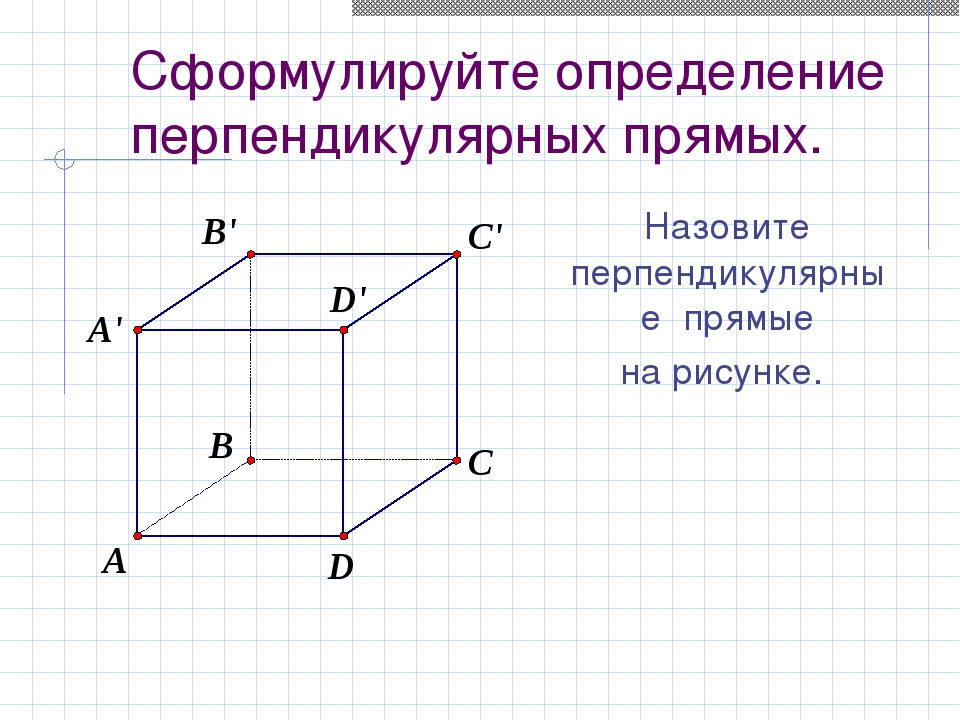
Сформулируйте определение перпендикулярных прямых. Назовите перпендикулярные прямые на рисунке.
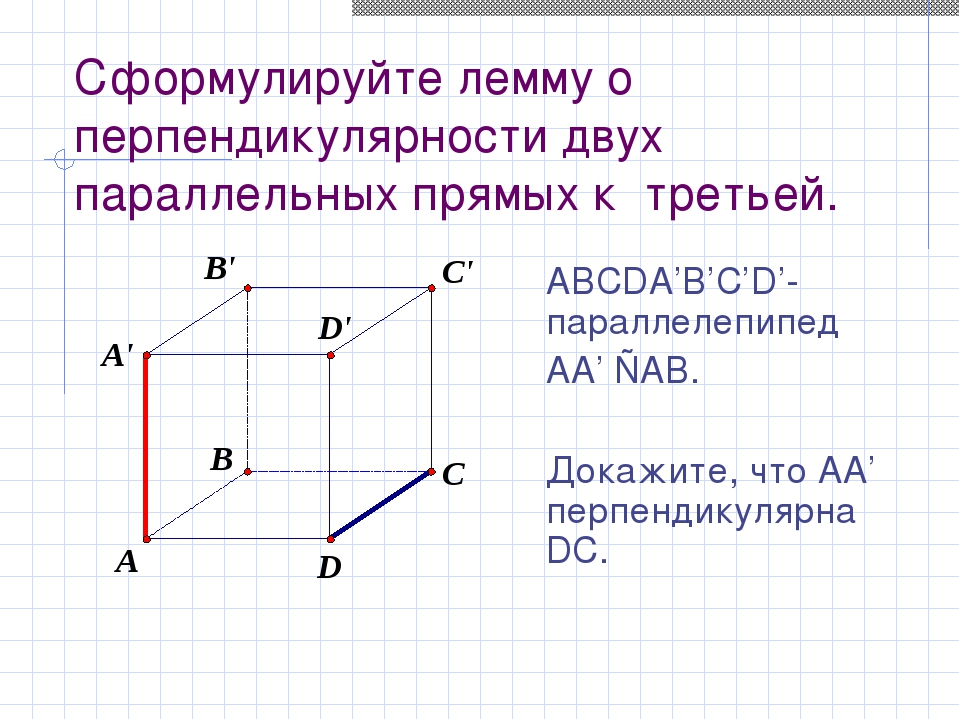
Сформулируйте лемму о перпендикулярности двух параллельных прямых к третьей. ABCDA’B’C’D’- параллелепипед AA’ ⊥AB. Докажите, что АА’ перпендикулярна DС.
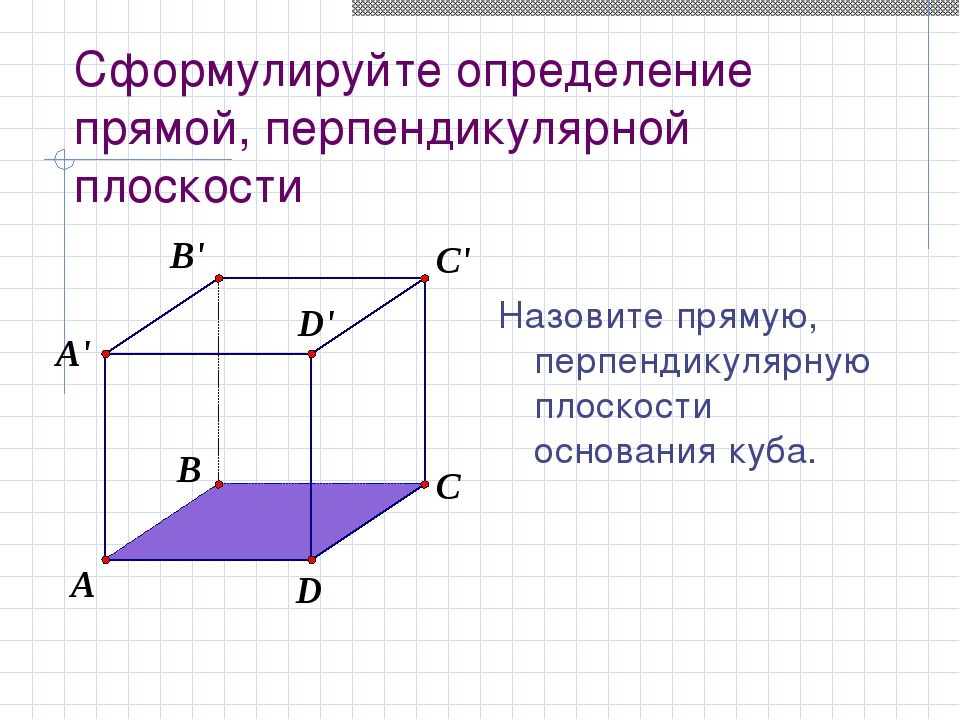
Cформулируйте определение прямой, перпендикулярной плоскости Назовите прямую, перпендикулярную плоскости основания куба.
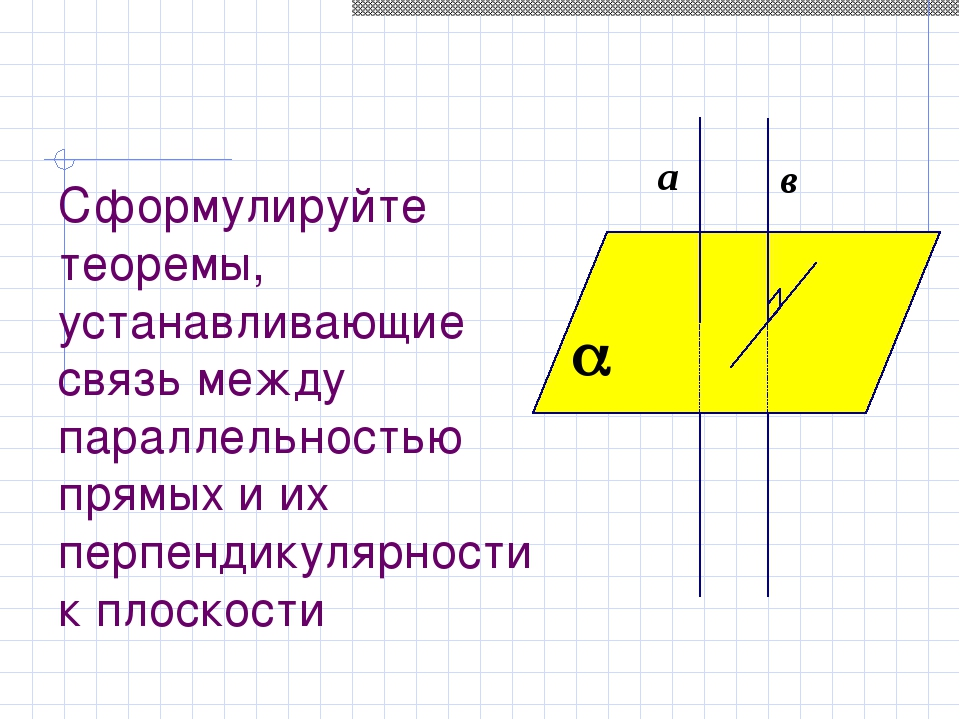
Сформулируйте теоремы, устанавливающие связь между параллельностью прямых и их перпендикулярности к плоскости
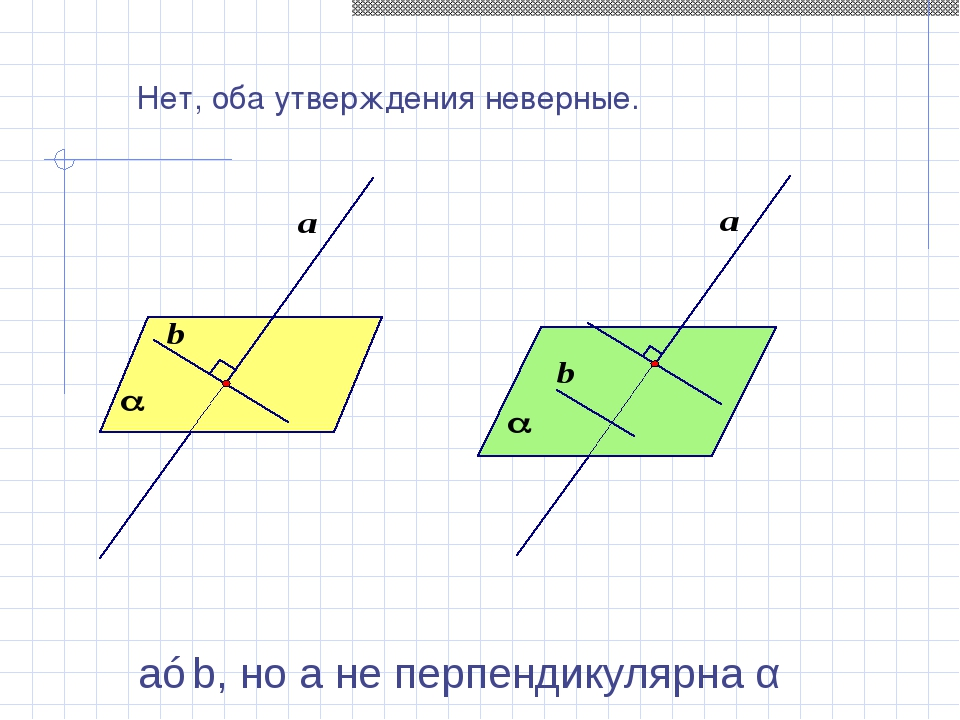
Верны ли утверждения: Прямая перпендикулярна плоскости, если она перпендикулярна какой–нибудь прямой, лежащей в этой плоскости? Прямая перпендикулярна плоскости, если она перпендикулярна параллельным прямым?
Признак перпендикулярности прямой и плоскости Если прямая перпендикулярна к двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна этой плоскости.
Прямая а проходит через центр круга. Можно ли утверждать, что прямая а перпендикулярна кругу, если 2.двум радиусам 1.она перпендикулярна диаметру 3.двум диаметрам
С М O В А 2 D В М O С А АВСD – квадрат со стороной 4, О – точка пересечения диагоналей. Найти расстояние от точки М до вершин квадрата. 1 4 4 4 4 АВС –равносторонний треугольник со стороной О – точка пересечения медиан. Найти расстояние от точки М до вершин треугольника.
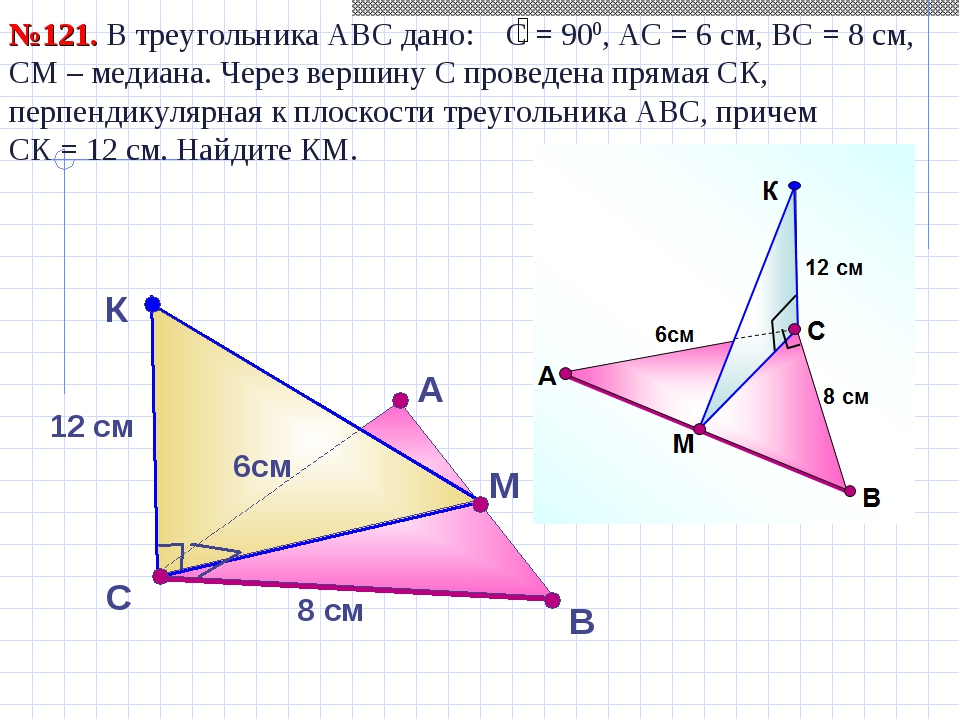
В №121. В треугольника АВС дано: С = 900, АС = 6 см, ВС = 8 см, СМ – медиана. Через вершину С проведена прямая СК, перпендикулярная к плоскости треугольника АВС, причем СК = 12 см. Найдите КМ. С А 12 см 8 см 6см
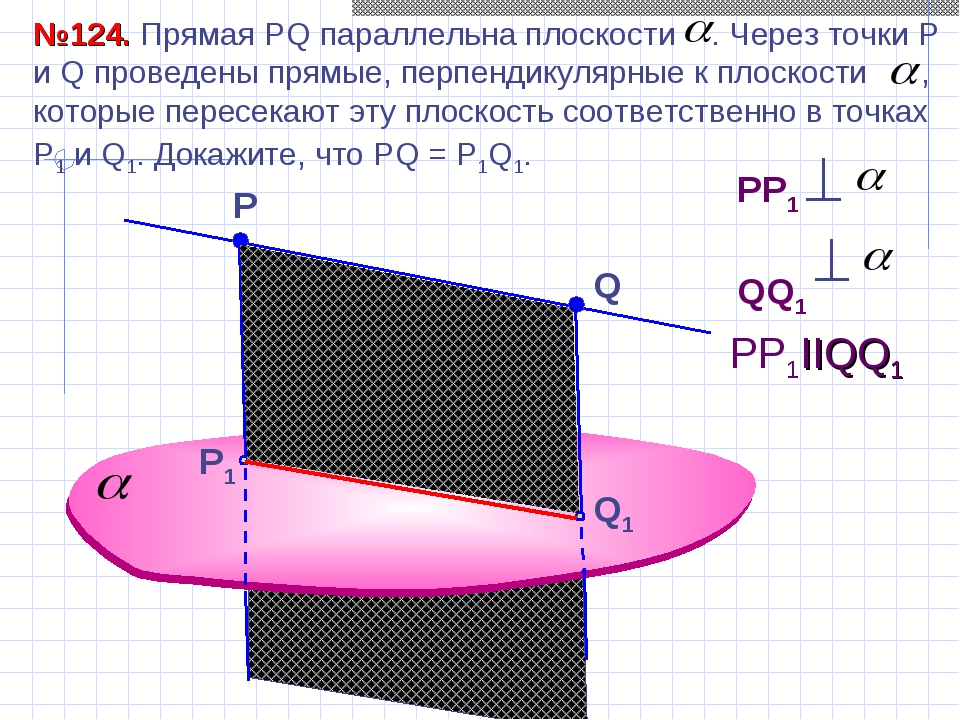
Р №124. Прямая РQ параллельна плоскости . Через точки Р и Q проведены прямые, перпендикулярные к плоскости , которые пересекают эту плоскость соответственно в точках Р1 и Q1. Докажите, что РQ = P1Q1. Q PP1IIQQ1

| Автор | |
|---|---|
| Дата добавления | 25.10.2019 |
| Раздел | Геометрия |
| Подраздел | Презентация |
| Просмотров | 2108 |
| Номер материала | 6388 |