
Творческая работа "Продвинутая медиана"
МОУ « Бегуницкая СОШ»
Творческая работа по геометрии ученицы 7а класса Кузиной Ульяны. Руководитель: учитель математики Боровкова О. В.
Продвинутая медиана
В городе Планиметрия в районе Треугольников на улице Равнобедренная переполох. Все только и говорят о наглой медиане, которая требует для себя привилегий. На базаре, на кухне, во дворе то и дело слышно: «Возмутительно! Что она о себе возомнила. Всего на всего обыкновенный отрезок, который соединяет вершину с противоположной стороной, а туда же – считает себя необыкновенной и особенной! Привилегии ей подавай…». Суды и пересуды не испугали продвинутую медиану. Она постоянно повторяла: « Я особенная, так как я не просто медиана, я медиана в равнобедренном треугольнике и проведена к основанию равнобедренного треугольника». Медианы, биссектрисы, высоты просто были в бешенстве. Чем она лучше…
Дело дошло до суда. Прокурор города не сомневался в своей победе. Он выведет эту плутовку на чистую воду. В треугольнике можно провести три медианы, почему медиана, проведенная к основанию равнобедренного треугольника должна иметь какие- то заслуги? Прокурор пользовался в городе большим авторитетом. Это был правильный четырехугольник, за острый ум все уважительно звали его квадратом. У квадрата и в голове и в поведении полный порядок: все стороны и все углы равны, даже диагонали пересекаются под прямым углом. Так как в квадрат можно вписать окружность и описать окружность около квадрата, то квадрат хорошо знал букву закона и сам выполнял все законы. Претензии медианы, по её утверждению, проведенной к основанию равнобедренного треугольника, о её исключительности безосновательны.
А кто судья? Судьей выступит окружность. Это неподкупная фигура. Как любят говорить в городе: «Эта фигура имеет центр и радиус. Любая прямая, проходящая через центр окружности - является осью симметрии. Наша окружность это- фигура, которая все вопросы решает только по закону!».
Защищать медиану вызвался отрезок. Да, у него есть свои достоинства - длина, ось симметрии, он часть прямой... Но тягаться с квадратом, сомнительное мероприятие. Никто в городе не верил в победу отрезка, так и говорили : «Против квадрата не попрёшь!».
И вот, наступил долгожданный день, на слушание дела собрался весь город. Шли как на праздник. Все хотели наказать эту выскочку – медиану.
Слово взял квадрат. Он приготовился к выступлению основательно. Объяснил присутствующим, какую фигуру называют треугольником, Дальше рассмотрел виды треугольников. Даже рассказал о периметре треугольника. Потом пояснил, какая точка называется серединой отрезка. Дал определение медианы треугольника. Объяснил, какие построения надо выполнить, чтобы получить медиану. Так же подробно квадрат остановился на биссектрисе и высоте. Подчеркнул, что в треугольнике можно провести три медианы, три биссектрисы и три высоты. Свое великолепное выступление квадрат закончил небольшим экзаменом присутствующих.. Назовите верное высказывание:
Биссектрисой треугольника называется ……………
луч, делящий угол на две равные части;
отрезок, делящий его угол на две равные части;
отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой пересечения противоположной стороны;
отрезок, соединяющий вершину треугольника с серединой противоположной стороны.
Все хором отвечали: отрезок, делящий его угол на две равные части;
Высотой треугольника называется………
перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону;
перпендикуляр, проведенный из вершины треугольника к противоположной стороне;
отрезок, соединяющий вершину треугольника с серединой противоположной стороны;
отрезок, делящий угол на две равные стороны.
Все хором отвечали: перпендикуляр, проведенный из вершины треугольника к противоположной стороне;
Медианой треугольника называется……….
перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону4
отрезок биссектрисы угла треугольника, делящий его на две равные части;
отрезок, соединяющий вершину треугольника с серединой противоположной стороны;
отрезок, делящий его на две равные части.
Все хором отвечали: отрезок, соединяющий вершину треугольника с серединой противоположной стороны.
Квадрат подытожил «У медианы нет никаких преимуществ!!!»
Зал аплодировал стоя. Блестяще! Грамотно! Великолепно!
Слово взял отрезок. После красивого и представительного квадрата он выглядел жалко. Он тоже обратился к залу. Найдите на рисунке треугольники, в которых проведены медианы, биссектрисы, высоты:
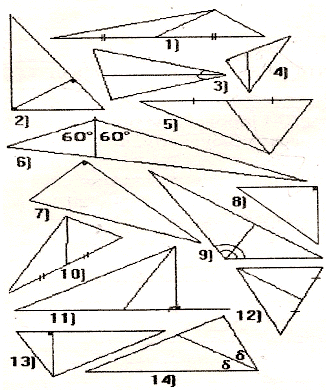
Из зала закричали: « Это знает любой семиклассник!»
Отрезок продолжал: « Правда. Это простой вопрос. Но здесь нет самого главного - равнобедренного треугольника. Вопрос в равнобедренном треугольнике. Возьмем равнобедренный треугольник и проведем к основанию равнобедренного треугольника медиану. Треугольник будет разбит на два равных треугольника». Треугольники в зале язвительно закричали: «Докажи!» Отрезок продолжал: « Треугольники равны по трём сторонам. Медиана разделила основание на два равных отрезка, боковые стороны равнобедренного треугольника равны, а сама медиана – общая для двух маленьких треугольников». В зале стояла гробовая тишина. Отрезок продолжал: « Если треугольники равны, то равны угли при вершине, лежащей против основания, это значит, медиана, проведенная к основанию равнобедренного треугольника, является биссектрисой. Из равенства треугольников следует равенство углов при основании , Это значит, что они прямые, следовательно, медиана есть высота. Получается, что медиана, проведенная к основанию равнобедренного треугольника является и медианой, и биссектрисой , и высотой. Такая медиана заслуживает привилегий!»
Судья окружность взяла молоточек и четко произнесла « Медиана, проведенная к основанию равнобедренного треугольника, является биссектрисой и высотой. Данная медиана заслуживает привилегий! Суд окончен» .
Медиана, проведенная к основанию равнобедренного треугольника ,получила привилегии. На её доме появилась мемориальная табличка, на которой золотыми буквами было написано: « Теорема: медиана, проведенная к основанию равнобедренного треугольника, является биссектрисой и высотой».
22.03 2017 год.

| Автор | |
|---|---|
| Дата добавления | 13.02.2019 |
| Раздел | Геометрия |
| Подраздел | Другое |
| Просмотров | 1519 |
| Номер материала | 6113 |