
Исследовательская работа по математике ученицы 9А класса "Нестандартные признаки равенства треугольников"
Российская Федерация
САМАРСКАЯ область, СЕЛО КИНЕЛЬ-ЧЕРКАССЫ
ГБОУ СОШ №2 «ОЦ» СЕЛА КИНЕЛЬ-ЧЕРКАССЫ
Научно-исследовательская работа
НЕСТАНДАРТНЫЕ ПРИЗНАКИ РАВЕНСТВА ТРЕУГОЛЬНИКОВ.
Секция «Математика»
Работу выполнила:
Иванова Анжелика, ученица 9А класса ГБОУ СОШ №2 «ОЦ»
с. Кинель – Черкассы
Научный руководитель:
учитель математики ГБОУ СОШ №2 «ОЦ» с. Кинель – Черкассы
Лукьянова Ольга Владимировна
Кинель – Черкассы, 2018 г.
Содержание
Введение………………………………………………………….…………3-4
Теоретическая часть.
Глава I. Признаки равенства треугольников…… …………………...5-8
Практическая часть.
Глава II. Нестандартные признаки равенства треугольников…...9-12
Глава III. Заключение……………………………………………………...13
Список литературы…………………………………………………………14
Приложение………………………………………………………………15-16
Введение.
Актуальность:
Треугольник – одна из основных фигур в планиметрии. При решении задач используют его самые разнообразные свойства. Свойства треугольника широко применяют на практике В архитектуре: при разработке чертежа здания, при планировке будущих квартир; в промышленности: при проектировании различных деталей, при изготовлении стройматериалов, при строительстве морских и авиа-судов; в навигации: для проложения правильного и максимально точного маршрута; а также в астрологии и астрономии, одним словом, просто необходимо знать треугольник и все его свойства. Одно из важнейших свойств для пары треугольников, устанавливать их равенство. При подготовке к ОГЭ по математике, я обратила внимание на то, что такого типа задачи встречаются как в первой части модуля «Геометрия» так и во второй (приложение 2). Чтобы решить задачи такого рода, просто необходимо знать признаки равенства треугольников. В учебнике геометрии, по которому мы обучаемся (авторы Л.С.Атанасян, В.Ф.Бутузов и др. Геометрия 7-9) рассматривается только три признака равенства треугольников.
Гипотеза: Возможно, ли сформулировать, кроме трёх известных, другие признаки равенства треугольников?
Чтобы убедиться в том, что ответ на этот вопрос волнует не только меня, я провела социологический опрос среди учащихся (приложение 1).
Мои предположения подтвердились. Большинство учеников знают только три признака равенства треугольников.
Цель: исследовать и сформулировать нестандартные признаки равенства треугольников.
Задачи:
Изучить литературу по исследуемой теме.
Уточнить количество признаков равенства треугольников.
Продемонстрировать другим учащимся существование других признаков равенства треугольников и возможности их доказательства.
Новизна: уточнение количества признаков равенства треугольников (анализ). Помимо трёх основных признаков равенства треугольников возможно указать немало других. Какие именно три соответствующих элемента нужно назвать для установления равенства треугольников?
Объект исследования: признаков равенства треугольников.
Предмет исследования: треугольник, как одна из основных фигур в планиметрии.
Методы исследования:
Теоретический (изучение, анализ и синтез),
системно-поисковый,
практический (доказательство теорем).
Глава I.
Теоретическая часть.
Признаки равенства треугольников.
Древнегреческий историк Геродот оставил описание того, как египтяне после каждого разлива Нила заново размечали плодородные участки его берегов, с которых ушла вода. По летописи Геродота, с этого началась геометрия – «землемерие». Такое название связанно с применением геометрии для измерений на плоскости. Древние землемеры выполняли различные геометрические построения, измеряли длинны и площади; астрологи рассчитывали расположение небесных светил, - всё это требовало весьма обширных познаний о свойствах плоских и пространственных фигур в первую очередь о треугольнике, его свойствах и признаках подобия и равенства треугольников.
Так какие же треугольники называются равными? Начнём с определения. Треугольники ABC и A1B1C1 называются равными, если они имеют соответственно равные стороны и углы.
Треугольник состоит из шести элементов. Из трёх углов и трёх сторон. При этом возникает вопрос: «Какое наименьшее количество элементов треугольника нужно взять для установления равенства двух треугольников?» Мы не сможем установить равенство двух треугольников по одному элементу, потому что неизвестно: «Будут ли равны остальные элементы?»
В В1
А С А1 С1
АС = А1С1
Так же невозможно установить равенство двух треугольников, используя два элемента по причине нехватки информации для установления равенства.
В
В1
А С А1 С1
АВ = А1В1, АС = А1С1.
Возможно установление равенства двух треугольников, используя три элемента. Но при этом возникает вопрос: «Какие именно три элемента нужно назвать, для установления равенства двух треугольников?»
При изучении этого вопроса, я просмотрела школьные учебники геометрии различных авторов, а также словари и справочники. В учебниках за седьмой класс предложены к изучению только 3 признака равенства треугольников:
Первый признак равенства треугольников. Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
Второй признак равенства треугольников.Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
Третий признак равенства треугольников.Если три стороны одного треугольника соответственно равны трём сторонам другого треугольника, то такие треугольники равны.
В справочнике по элементарной математике М.Я.Выгодского был предложен четвёртый признак равенства треугольников :
Если две стороны и угол, лежащий против большей из них одного треугольника соответственно равны двум сторонам и углу, лежащему против большей из них другого треугольника, то такие треугольники равны. Приведу одно из предложенных доказательств этого признака.
Дано: ∆ АВС, ∆ А1В1С1, АВ = А1В1, АС= А1С1., ے В = ے В1.
Доказать: ∆ АВС = ∆ А1В1С1.
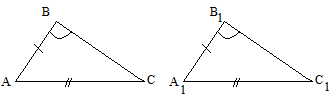
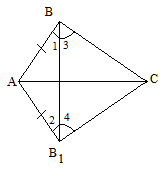
Рисунок № 1
Доказательство: расположим треугольники так, как на рисунке 1. Соединим В и В1, тогда ∆АВВ1 – равнобедренный, значит ے 1= ے 2. ے 3= ے 4 как остатки равных углов. Получим ∆ВСВ1 – равнобедренный, отсюда ВС=В1С. ∆АВС=∆А1В1С1 по трем сторонам.
Также в школьном курсе рассматриваются четыре признака равенства прямоугольных треугольников:
Первый признак равенства прямоугольных треугольников. Если катеты одного прямоугольного треугольника соответственно равны катетам другого, то такие треугольники равны.
Второй признак равенства прямоугольных треугольников. Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого, то такие треугольники равны.
Третий признак равенства прямоугольных треугольников. Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого, то такие треугольники равны.
Четвёртый признак равенства прямоугольных треугольников. Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого, то такие треугольники равны.
Глава II.
Практическая часть.
Я решила расширить теоретическую базу по признакам равенства треугольников, добавив к сторонам и углам, используемым в классических признаках равенства треугольников, другие компоненты: биссектрису, медиану и высоту.
Нестандартные признаки равенства треугольников.
1) По двум сторонам и высоте, проведенной к одной из них.
A
B K C
A1
B1 K1 C1
Дано: АВ = А1В1, ВС = В1С1, АК = А1К1.
Доказать: ∆АВС=∆А1В1С1
Доказательство: ∆АВК= ∆А1В1К1 по гипотенузе и катету, тогда ےВ = ےВ1 и получим ∆АВС = ∆А1В1С1 по 1 признаку (по 1 признаку).
2) По двум сторонам и медиане, проведенной к одной из них.
В В1
К К1
А
С А1 С1
Дано: АВ = А1В1, ВС = В1С1, АК = А1К1. АК иА1К1- медианы
Доказать: ∆АВС=∆А1В1С1.
Доказательство: ∆АВК= ∆А1В1К1 по трем сторонам, значит ےВ = ےВ1 и
∆АВС = ∆А1В1С1 по 1 признаку
3)По двум углам и высоте, проведенной из третьего угла
А A1
B K C B1 K1 C1
Дано: ےВ = ےВ1 , ےС = ےС1.AK=A1K1
Доказать: ∆АВС=∆А1В1С1.
Доказательство: ∆АВК= ∆А1В1К1 по катету и острому углу, значит BK= B1K1 ∆АСК= ∆А1С1К1 по катету и острому углу, значит KC=K1C1 , а следовательно
BC=B1C1 , а ∆АВС = ∆А1В1С1 по 2 признаку.
4) По стороне и двум высотам, проведенным из углов, прилежащих к этой стороне.
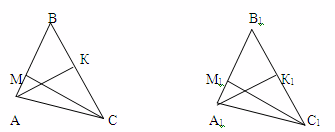
Дано: АС = А1С1, СМ = С1М1, АК = А1К1.
Доказать: ∆АВС=∆А1В1С1.
Доказательство: ∆АМС= ∆А1М1С1 по катету и гипотенузе, значит угол А равен углу А1,,а ∆АКС = ∆А1К1С1 по катету и гипотенузе, значит ےС = ےС1 Итак, ∆АВС = ∆А1В1С1 по 2 признаку.
5) По двум сторонам и высоте, проведенной к третьей стороне.
Дано: АВ = А1В1, ВС = В1С1, ВК = В1К1.
Доказать: ∆АВС=∆А1В1С1 .
Доказательство: ∆АВК= ∆А1В1К1 по гипотенузе и катету, значит АК=А1К1 ∆ВКС = ∆В1К1С1 по катету и гипотенузе, значит КС=К1С1. Итак, ∆АВС = ∆А1В1С1 по трем сторонам.
В В1
А К С А1 К1 С1
6) По стороне, одному из углов, прилежащих к этой стороне и биссектрисе из этого угла.
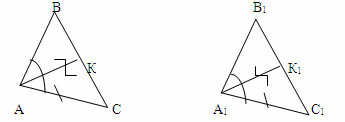
Дано: АС = А1С1, АК = А1К1, ےА = ےА1.
Доказать: ∆АВС=∆А1В1С1.
Доказательство: ∆КАС = ∆К1А1С1 по 1признаку, отсюда
ےС = ےС1, ∆АВС = ∆А1В1С1 по 2признаку.
7) По двум высотам и углу, из которого проведена одна из высот.
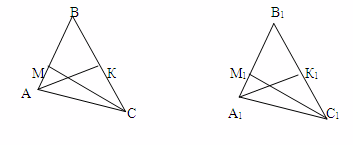
Дано: СМ = С1М1, АК = А1К1, ےА = ےА1.
Доказать: ∆АВС=∆А1В1С1.
Доказательство: ∆АМС= ∆А1М1С1 по катету и острому углу, ∆АКС = ∆А1К1С1 по катету и гипотенузе, ∆АВС = ∆А1В1С1 по 2признаку.
Глава III
Заключение.
В ходе исследования я выяснила, что помимо трех основных признаков равенства треугольников возможно отыскать немало других. Я сформулировала и доказала равенство треугольников по медиане, высоте, биссектрисе треугольника в сочетании со сторонами и углами треугольника, придерживаясь наличия трех элементов, таким образом, убедилась в том, что моя гипотеза верна.
Вывод: в результате моего исследования были сформулированы и доказаны несколько признаков равенства треугольников, не изучаемых в школьном курсе геометрии, но облегчающих решение задач подобного типа при подготовке к ОГЭ по математике.
Список литературы:
Выгодский М.Я. Справочник по элементарной математике.
Геометрия. 7-9 классы: учеб. Для общеобразоват. учреждений/Л.С.Атанасян, В.Ф.Бутузов, С.Б. Кадомцев и др. – 19-е изд. – М. : Просвещение, 2009.
Погорелов А. В. Геометрия: Учеб. Для 7-9 кл. общеобразоват. Учреждений. – 3-е издание. – М.: Просвещение, 2002.
Интернет-ресурсы.
Приложение 1
Анкетирование.
1.Как вы считаете, сколько существует признаков равенства треугольников?
А) 3 Б) более трех В) меньше трех
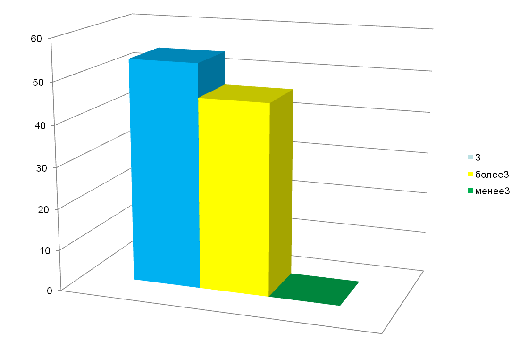
2. Хотели бы вы узнать новые признаки равенства треугольников?
А) да Б) нет

Приложение 2.
Типовые задачи на признаки равенства треугольников из тренировочных КИМ для подготовки к ОГЭ по математике, модуль «Геометрия»


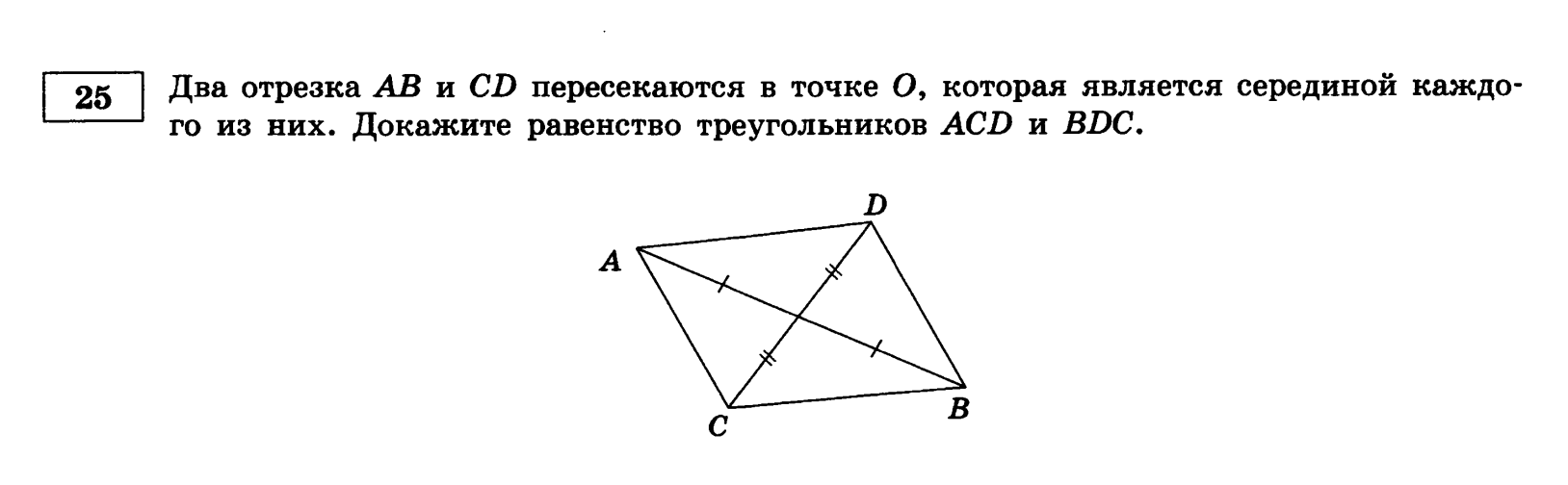
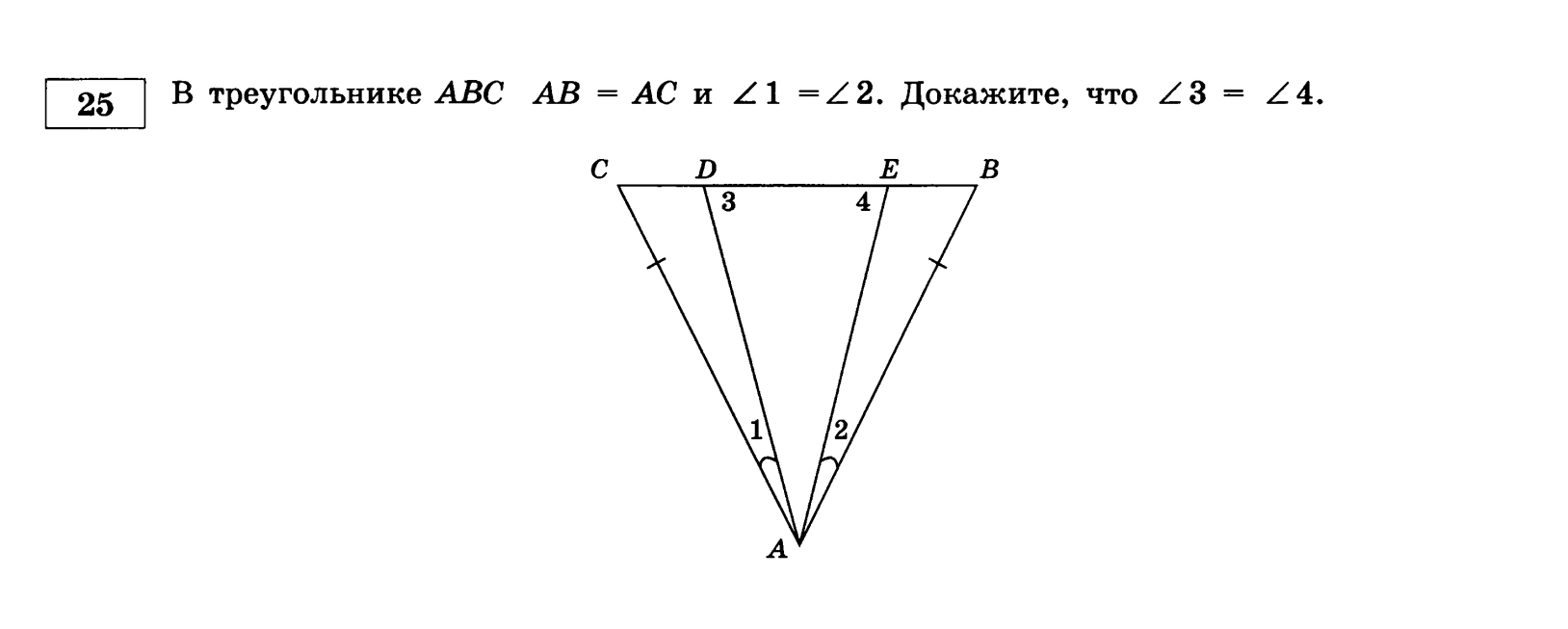

| Автор | |
|---|---|
| Дата добавления | 05.11.2018 |
| Раздел | Геометрия |
| Подраздел | Научная работа |
| Просмотров | 2036 |
| Номер материала | 5917 |