
Урок "Функция. Область определения и область значений функции"

Краткое описание документа:
Тема «Функция. Область определения и область значений» изучается у курсе алгебры 9 класса. Автор данного урока предлагает свою разработку, которая может стать помощником каждому учителю математики. Ведь, благодаря ей, свое свободное время можно посвятить другим делам, нежели придумывать какие-то новые и интересные способы преподнесения информации, нового материала школьникам.
Данный урок длится 6:05 минут. Он начинается с того, что определяется понятие функции. На экране появляется определение, которое выделено яркой рамкой. Затем автор расшифровывает, что такое xи y.
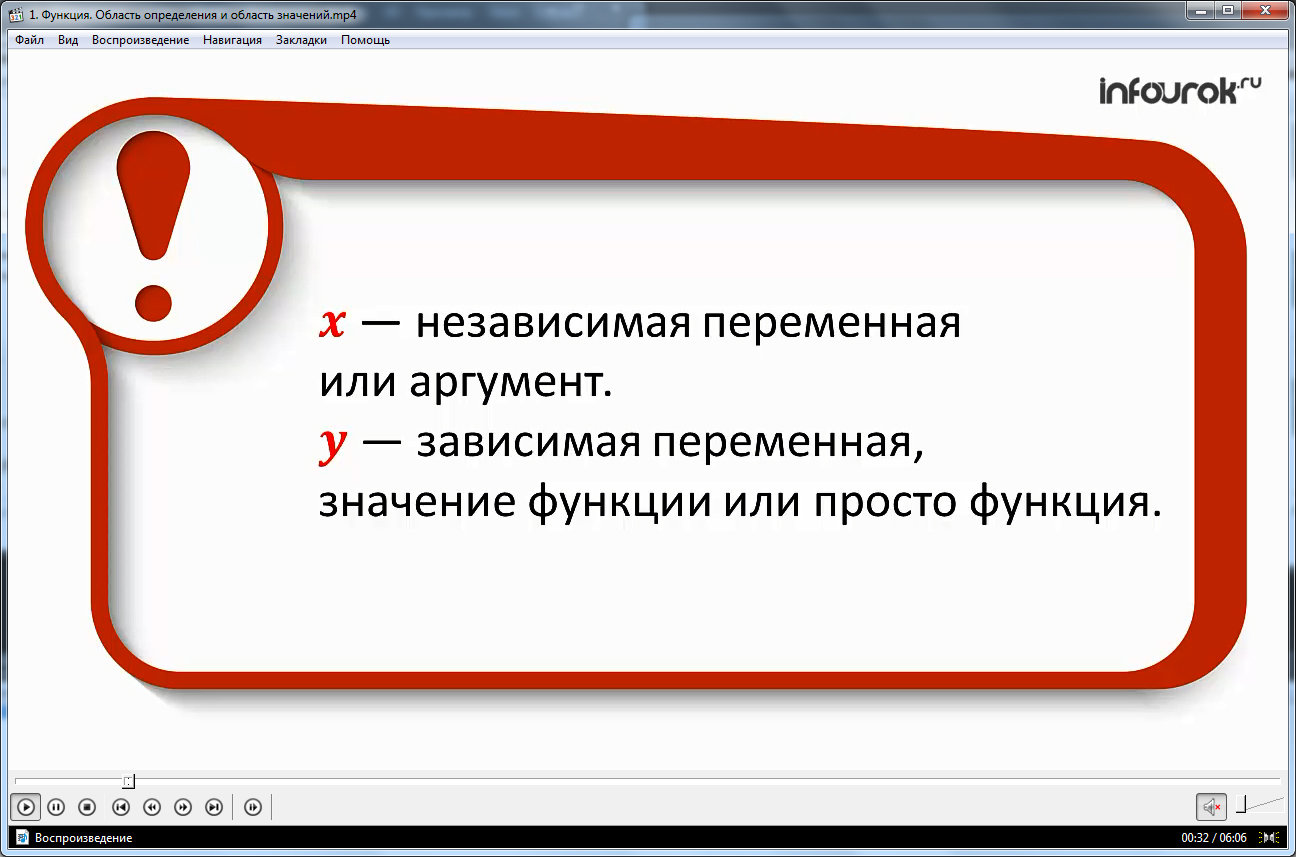
Далее автор демонстрирует слушателям, как записывается функция на математическом языке. Здесь же поясняется, как обозначается значение функции.
После этого следует пример, где автор показывает, как используется только что предоставленная информация. То есть функция записывается через введенное только что обозначение. И в этом же примере предлагается найти значение функции, если даны два значения переменной. Ниже прилагается подробное решение поставленной задачи. Автор подробно расписывает то, как находится значение функции при известных значениях переменной.
Если до этого говорилось, что функция может быть записана в виде f(x), то здесь автор обращает внимание на то, что вместо буквы fможет стоять любая строчная буква латинского или греческого алфавита.
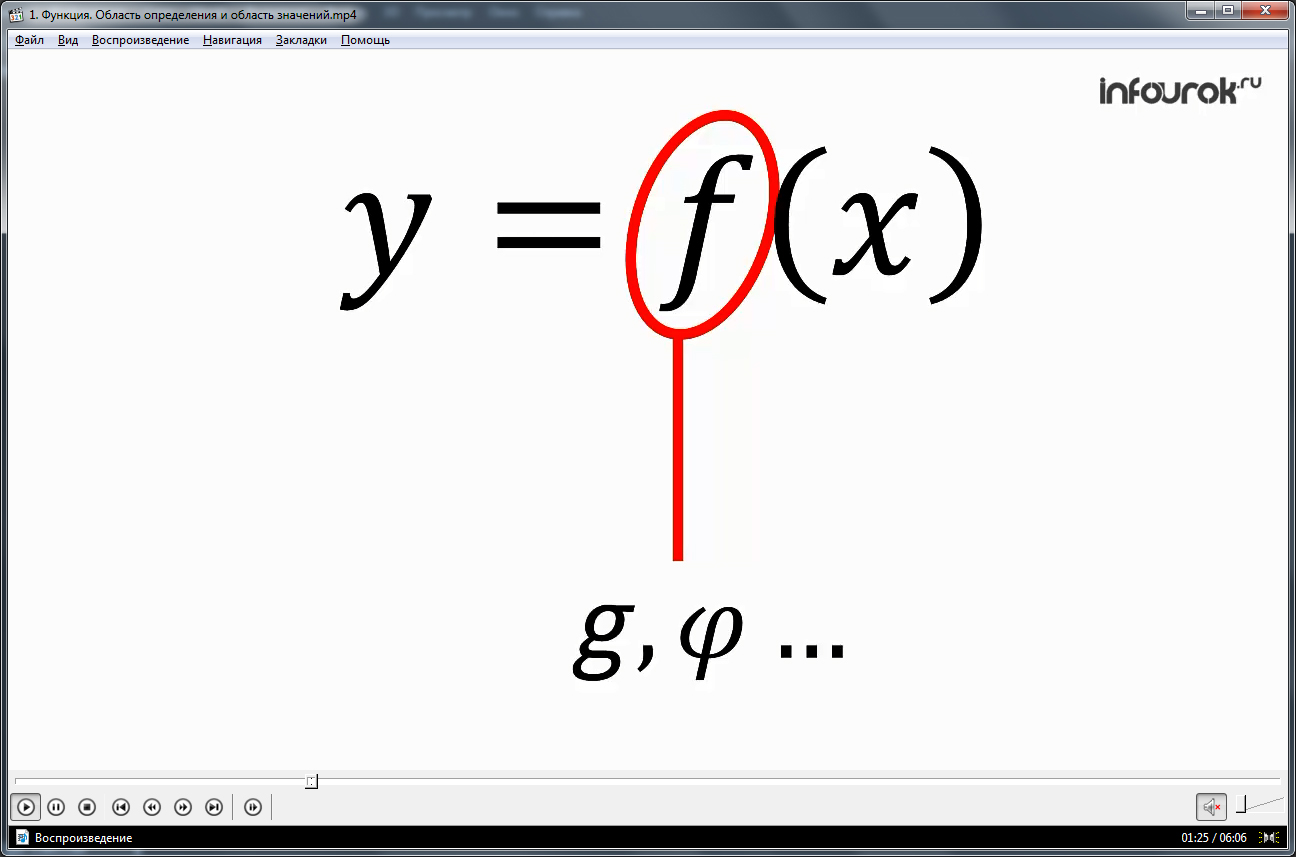
После этого происходит знакомство с понятиями области определения функции и ее области значений. Эти определения заключены в ярко выделенную рамку. Также на экране показано, как обозначаются область определения и область значения функции.
Затем автор поясняет, в каком случае функция считается заданной. Затем идет пояснение того, что область определения строится из всех значений переменной x, если эта область не указана иначе.
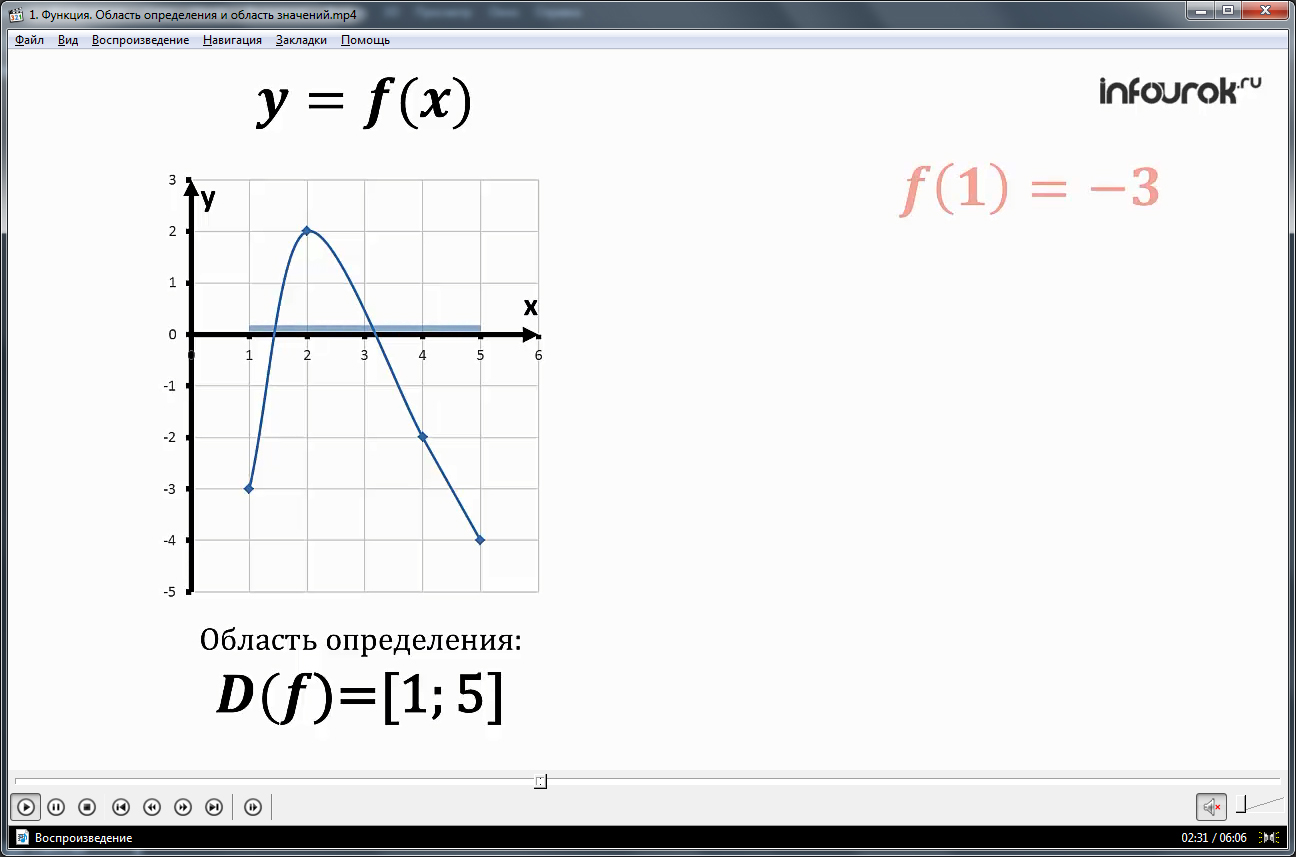
Далее следует определение понятия графика функции. После этого определения автор предлагает рассмотреть пример графика функции, который изображен на рисунке. Здесь задана область определения в виде отрезка. Далее говорится о том, что значение функции в любой точке из области определения можно найти с помощью этого графика. Для этого автор берет определенные значения переменной и находит для них значения функции. При этом находится наибольшее и наименьшее значения заданной функции в данной области определения. Так автор показывает, что эти значения функции являются граничными, а между ними заключается область значения заданной функции.
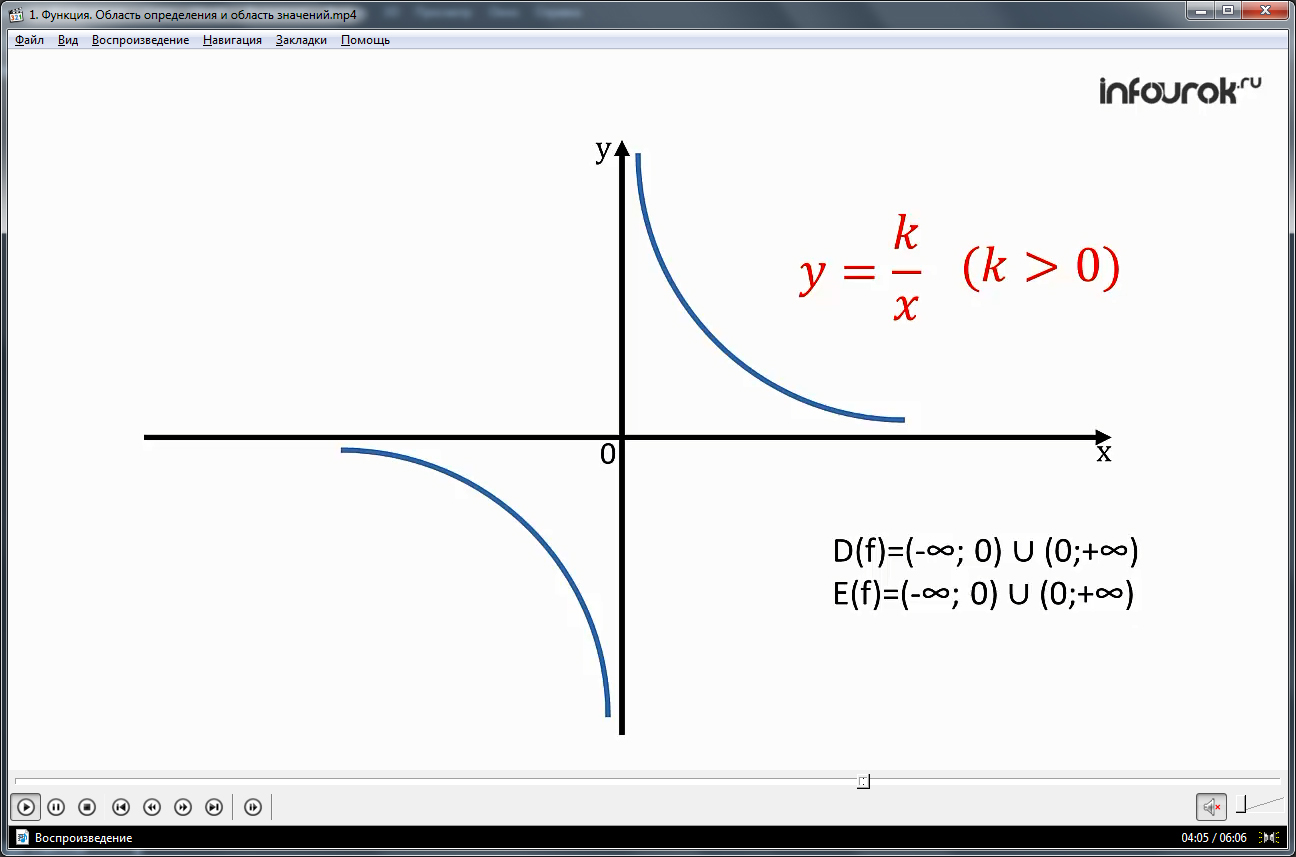
Далее автор говорит о том, что ранее обучающиеся уже знакомились с некоторыми видами функций. Речь идет о линейной функции, о прямой и обратной пропорциональностях. Он тут же напоминает, что это за функции, как они выглядят, как записываются. Далее автор демонстрирует графики этих функций, а затем поясняет, какие они имеют области определения и области значений.
После того, как рассмотрены различные функции, автор замечает, что функцией записываются многие реальные процессы и закономерности. В качестве примера он использует зависимость массы тела от его объема, говоря, что эта зависимость является прямой пропорциональностью. Следующий пример показывает, как зависит длина окружности от ее радиуса. Пример зависимости силы тока на участке цепи от сопротивления проводника при постоянном напряжении показывает обратную пропорциональность. Этой же закономерностью описывается зависимость времени, затраченного на прохождение заданного пути, от скорости движения.
После рассмотренных примеров, автор возвращается к повторению тех функций, которые также изучались ранее. А именно это функции , и . Показаны их графики.
Далее рассматривается функция. Находится ее область определения, которая позволяет разбить данную функция на две. Но так как область определения является областью для первоначально заданной функции, то эти две функции объединяются, и получается новое задание функции, с помощью системы. Затем строится график этой функции.
На этом вся теоретическая часть заканчивается. Остальное остается за учителем. Ему необходимо подобрать задания для закрепления только что изученного материала.
| Автор | |
|---|---|
| Дата добавления | 29.08.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 10853 |
| Номер материала | 691 |