
Урок "Как построить график функции у=f(x)+m, если известен график функции у=f(x)"

Краткое описание документа:
Для того, чтобы успешно решить множество вариантов уравнений и выражений, связанных с графиками различных видов функций, необходимо научиться быстро и безошибочно находить график любой зависимости. Существует достаточно большое количество типов функций и соответствующих им графиков. В математике школьного курса широко применяются лишь несколько основных видов – прямая зависимость, графики квадратичной и кубической функции, а также тригонометрические зависимости. Последние не рассмотрены в представленном видеоуроке, так как имеют определенные отличия и несколько иные правила, которые не позволяют этим зависимостям соответствовать общим законам.
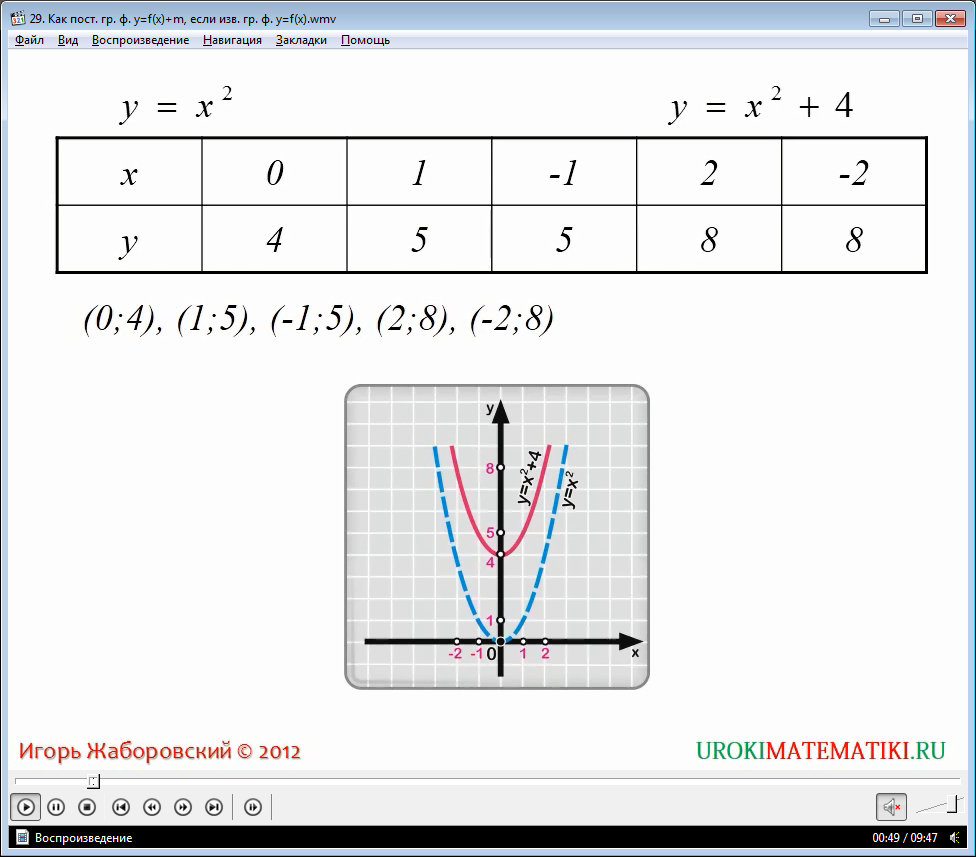
Мы не будем в этом видео рассматривать тонкости построения каждого элементарного графика, а пристально изучим зависимости, которые отличаются от типичных графиков определенным добавочным коэффициентом.
Рассмотрим, к примеру, функцию вида y = x +5. Это линейная зависимость, очень похожая на функцию y = kx. Как мы помним из предыдущих видеоуроков, график этой типичной зависимости представляет собой прямую линию, проходящую через центр координатной сетки (нулевую точку). Что поменяется в графике при добавлении значения «+5»? Чтобы это выяснить, в видеоуроке был визуализирован график по рассчитанному набору значений х и у. При этом, функция y = x +5 имеет график в виде такой же прямой линии, под тем же углом к оси абсцисс, но она несколько сдвинута вверх, по оси ординат, а именно на 5 единиц. То есть, если в линейной зависимости после переменной существует добавочный алгебраический элемент с положительным знаком, то график функции просто параллельно поднимается вверх по оси у, на значение, равное добавочному элементу. Иначе говоря, если у = kx + b, то график такой функции будет прямой линией, подобной графику у = kx, перенесенной на b единиц вверх.
Нетрудно сообразить, что при отрицательном добавочном элементе прямая спустится вниз по оси ординат, на значение этого элемента. Таким образом, сохраняется универсальность применения данного правила. Любая функция, которая в процессе преобразований сводится к зависимости вида у = kx +/- b
имеет график в виде прямой линии, лежащий на b единиц выше, или ниже центра координат.
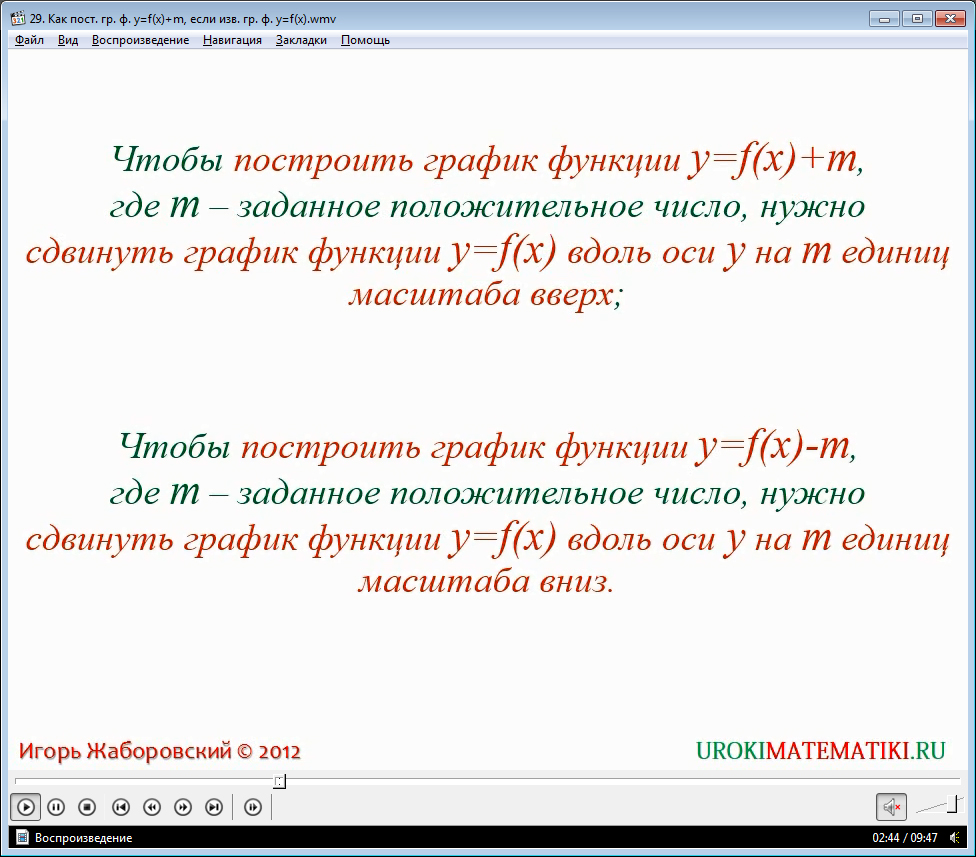
Рассмотрим на примерах данного видеоурока другой тип функции, а именно – зависимость вида у = kx2 + m. Нам уже известно, что графиком данной функции является особая фигура, именуемая параболой. Ветви параболы выходят из центра координат и пролегают вдоль линии ординат. При этом, если значение k при х положительное, то парабола направлена ветвями вверх, в положительную часть оси у. Если k отрицательно, то парабола «перевернута» ветвями вниз, в отрицательные четверти ординат. Общее правило смещения работает и в данном случае – в зависимости от знака при значении m, центр параболы сдвигается вниз (если m отрицательна), или же вверх, на количество единиц m. Таким образом, во многих случаях, добавочный алгебраический элемент m смещает график функций на свое значение, в зависимости от знака. При этом форма графика остается неизменной.
Умение быстро строить графики различных функций весьма пригодится в решении определенных задач. Как описано в видеоуроке, существуют задачи следующих видов:
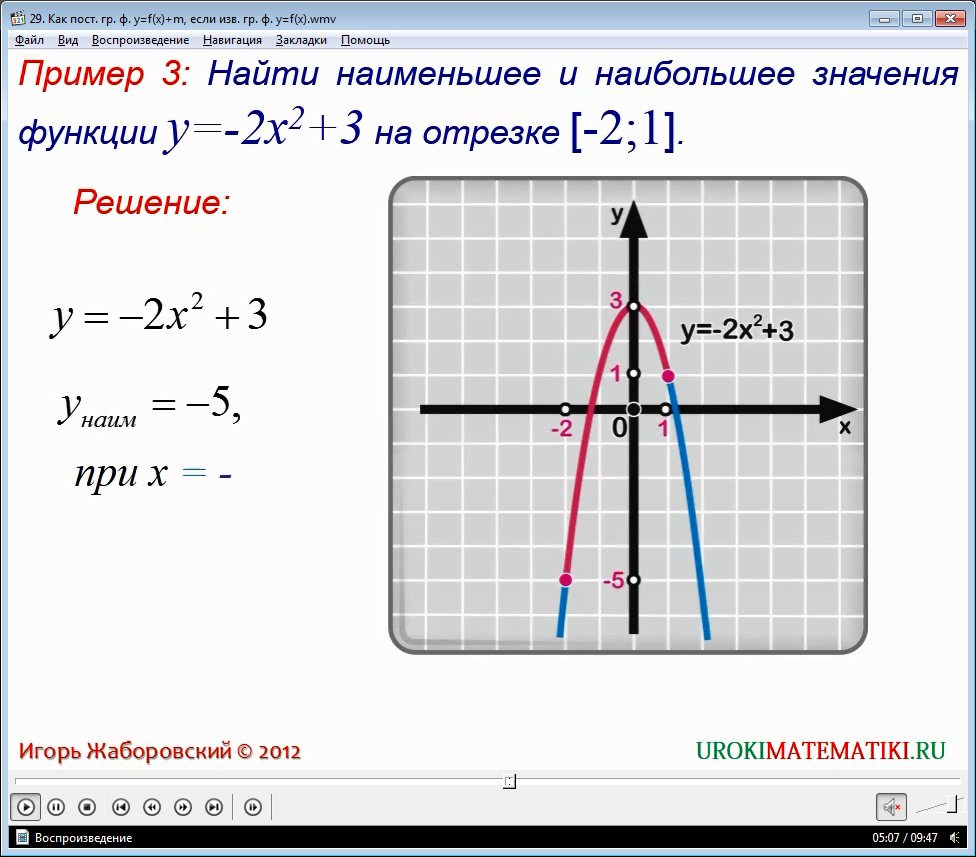
Пример 1: Решите уравнение x2 +1 = 2/x
Решать данное выражение методами линейной алгебры крайне затруднительно, поэтому воспользуемся способом построения графиков. У нас есть два выражения, разделенных знаком равенства – разобьем их на две функции:
x2 +1 = 2/x
y = x2 +1
y = 2/x
Графиком второй функции является обычная гипербола. А вот для построения графика первой зависимости нам нужно не просто нарисовать параболу вида
y = x2, но и сместить её на единицу вверх, по оси ординат, согласно вышеизложенному правилу. Построив оба графика в декартовой сетке (что иллюстрируется на видео), мы можем заметить, что они пересекаются в строго определенной точке, характеризующейся координатами (2,1). Второе значение (х) и есть наша неизвестная переменная.

Действительно:
x2 +1 = 2/x
12 + 1 = 2/1
2=2
Стоит отметить также, что подход к построению графиков функций вида
y = a/(x + m) точно следует описываемому правилу, то есть, изначально выстраивается двойная гипербола, которая параллельно сдвигается на m единиц.
| Автор | |
|---|---|
| Дата добавления | 30.07.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 5571 |
| Номер материала | 552 |