
Урок "Как построить график функции у=f(x+l), если известен график функции у=f(x)"

Краткое описание документа:
В этом видеоуроке будет рассмотрен вопрос графического представления функции y = f(x + l), при условии, что график функции y = f(x) известен заранее.
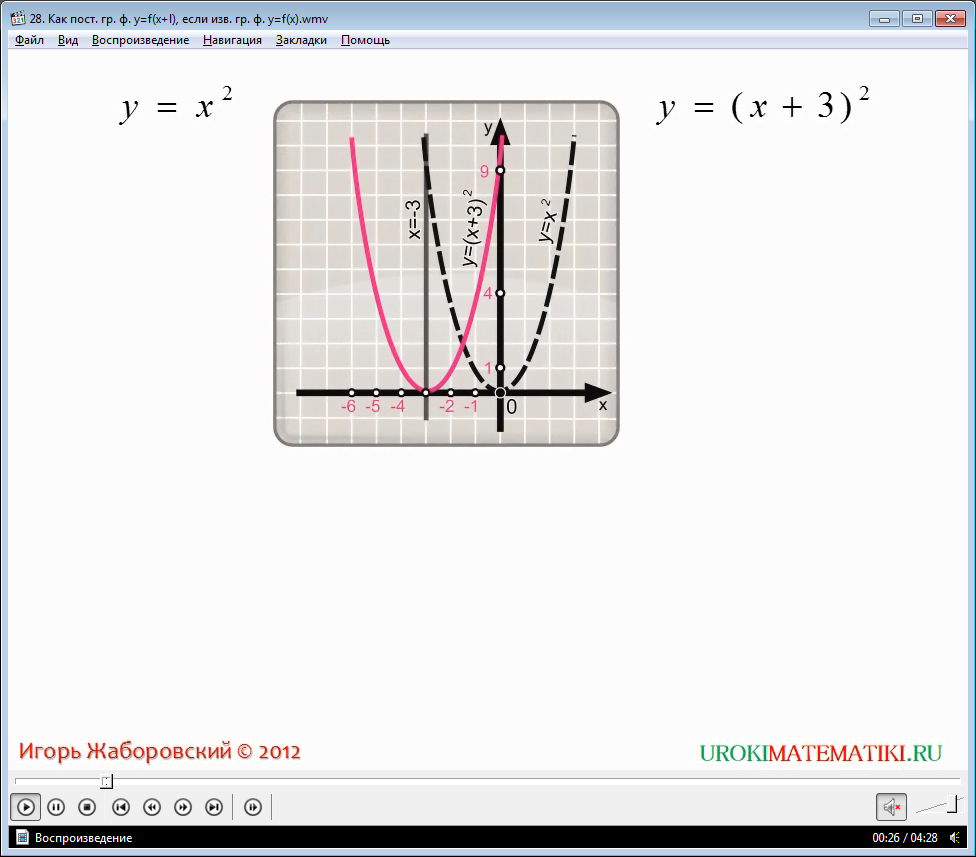
Для полноты понимания, объяснения будут сопровождаться визуальным дополнением. Для этого построим графики функций у = х2 и у = (х + 3)2 в одной системе координат. Первая из функций уже была рассмотрена в наших видеоуроках ранее, и мы знаем, что ее график – это парабола. Для функции у = (х + 3)2, подставляя значения аргумента х, рассчитываем координаты точек, по которым и строим график. Соединив точки плавной кривой, мы видим, что график являет собой параболу. Можно заметить, что этот график имеет такой же вид, что и в случае у = х2, однако в этом случае он перемещен влево на три единицы по оси абсцисс. Соответственно, наблюдается и смещение вершины параболы в положение (- 3; 0), а не в начале координат, как это наблюдаем у параболы равенства у = х2. Ось симметрии также смещена, и соответствует линии в положении х = - 3, а не х = 0, как это мы можем наблюдать в случае графика уравнения у = х2.
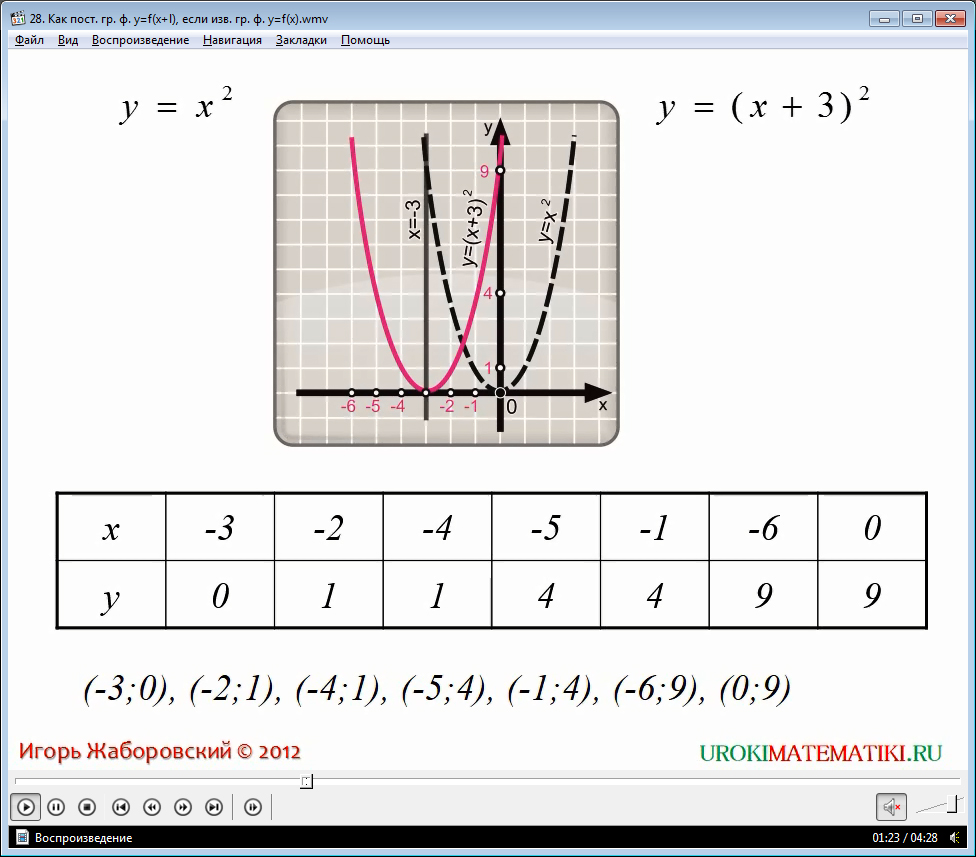
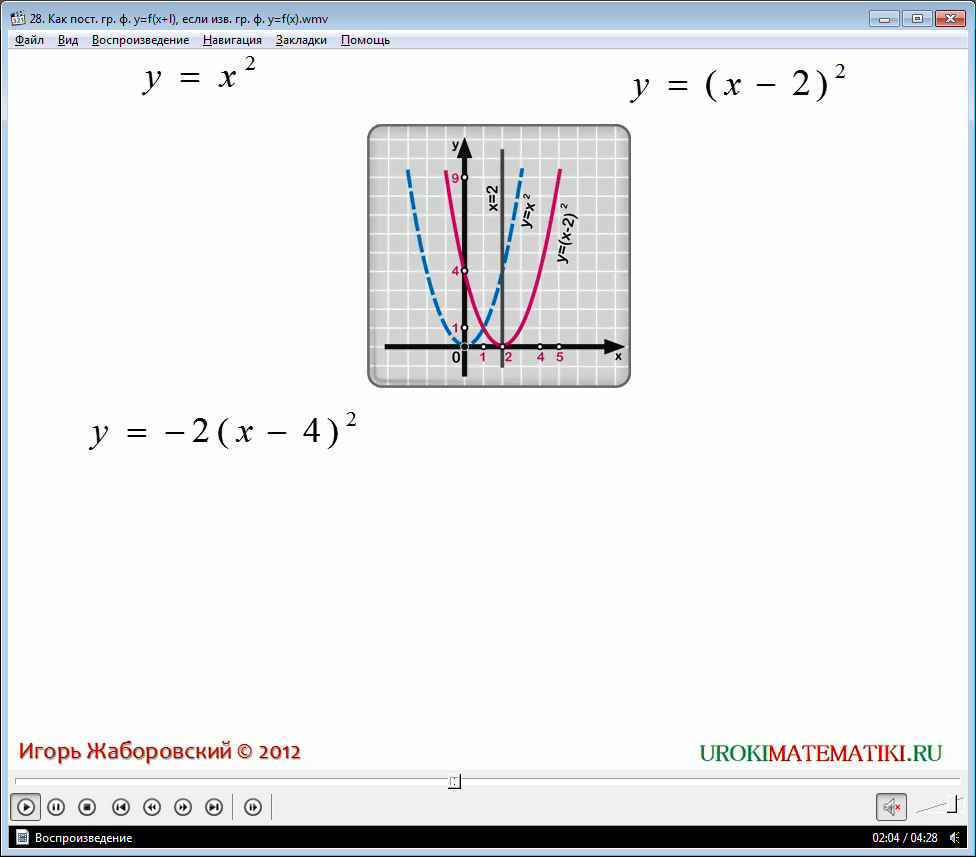
Когда мы изображаем, как демонстрирует видео, графики функций у = x2 и у = (х - 2)2 в одной координатной сетке, можно заметить, что второй график похож на первый с той лишь особенностью, что наблюдается смещение по оси абсцисс вправо на 2 позиции. Как это выглядит воочию, вы можете увидеть в предложенном видеоматериале.
После просмотра этого примера становится ясно, что графически решения функций данного типа происходят по тому же алгоритму.
Еще один пример, который предлагает наше видео, - это равенство у = -2 (х - 4)2. Ее графиком также является парабола вида y = - 2x2, претерпевшая сдвиг, то есть параллельный перенос вдоль оси абсцисс вправо на четыре единицы. С самим графиком вас познакомит это видео.
Исходя из изложенного выше, можно сделать следующие выводы:
1) Для того чтобы начертить график функции типа у = f(x + l), в случае если l - это положительное число, заданное условием, необходимо переместить график равенства по оси х влево на l единиц масштаба;
2) Для того, чтобы построить график функции у = f(x - l), где число l - это заданное положительное число, то нужно график функции у = f(x) просто сдвинуть вдоль оси х на l единиц масштаба вправо.
То есть, если знак числа l положительный, то смещаем в направлении убывания значений по оси абсцисс, а если отрицательный, то в сторону увеличения.
Далее рассмотрим несколько примеров
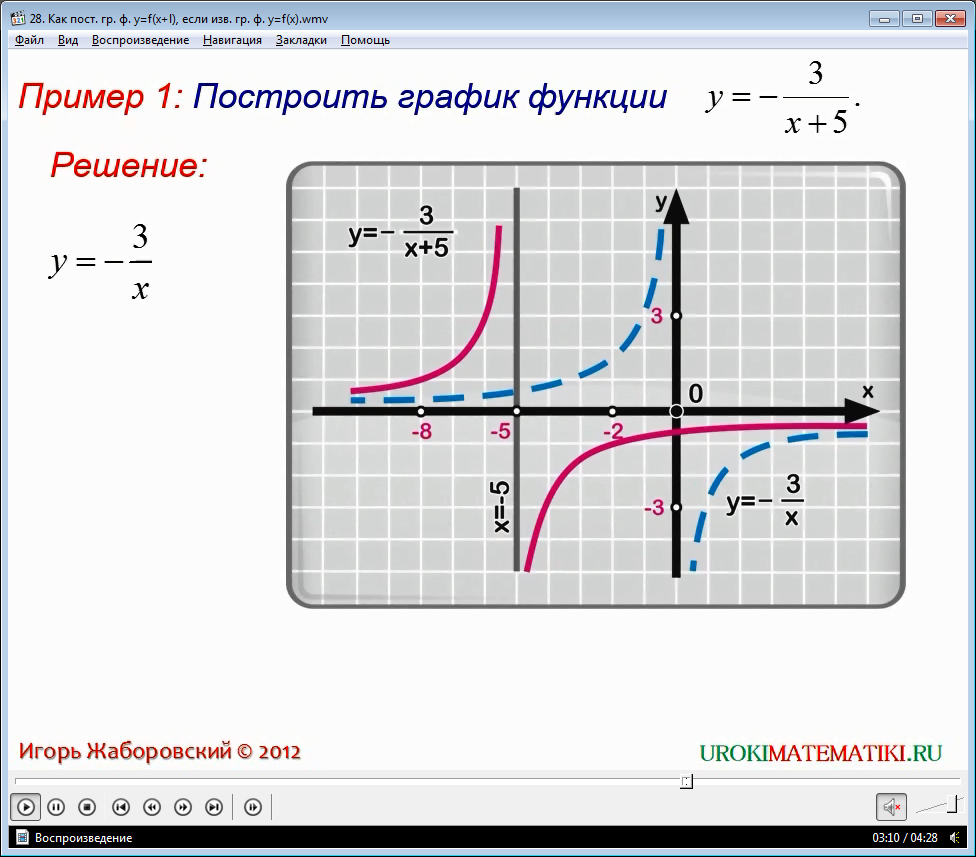
Пример 1. Используя полученные в видеоматериале знания, необходимо построить график функции y = - 3 / (x+5)
Для решения этой задачи сначала строим гиперболу для равенства y = -3/x, после этого сдвигаем полученный график вдоль оси абсцисс влево на 5 единиц масштаба. В результате чего у нас получился требуемый график – это гипербола с асимптотами х=-5 и у = 0. Сам график вы видели при просмотре предложенного видео.
Следующий пример состоит в следующем: необходимо построить график функции у = |х+2|. Суть решения данной задачи имеет такой же алгоритм, что и в предыдущем случае. Сначала строим график функции у = |х|, а затем сдвигаем его на две единицы масштаба влево.
В дополнение следует сказать, что при построении графика функции вида у = f(x + l), в случае если l – это любое число, отличительное от нуля, то есть как положительное, так и отрицательное. При решении задач функций мы рассчитывали координаты точек, по которым и строили графики, не обращая внимания на знак возле некоего числа l, которое присутствовало в наших функциях, а просто отмечали сдвиг графика в той или иной мере. Однако следует отметить, что направление сдвига все же определялось именно знаком числа l: в случае, когда значение числа l было положительным, график сдвигался влево, а в случае, когда число l было меньше нуля, график сдвигался вправо.
| Автор | |
|---|---|
| Дата добавления | 30.07.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 8094 |
| Номер материала | 551 |