
Урок "Функция y=k/x и ее график"

Краткое описание документа:
В этом видеоуроке вы познакомитесь с функциейy = k/x, k – коэффициент, который может принимать разные значения, кроме 0. Давайте рассмотрим случай, когда k = 1 => y = 1/x. Для построения графика этой функции вспомним материал, который был в предыдущих видео, а именно: подберем для x несколько произвольных значений и подставим их в формулуy = k/x.
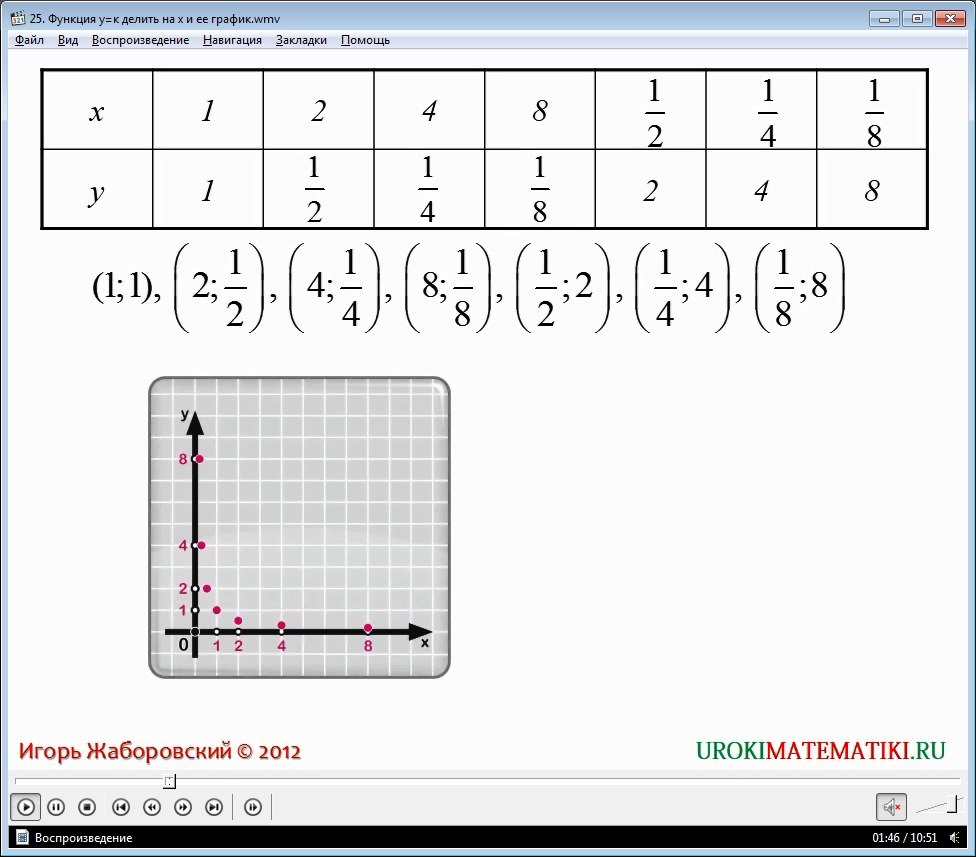
Это даст нам возможность вычислить значения зависимой переменной y. Подбор значений и вычислений y построим в два этапа: сначала придадим аргументу положительные значения, а потом – отрицательные.
- Пользуясь формулой y = k/x, найдем значение y. Если x = 1 , то y = 1. Подберем несколько аргументов самостоятельно.
В случае, когда x = 3, то y = 1/3; х = 5, то у = 1/5; х = 7, то у = 1/7.
И когда х = 1/3, то у = 3; х = 1/5, то у = 5; х = 1/7, то у = 7.
Составим таблицу:
|
х |
1 |
3 |
5 |
7 |
1/3 |
1/5 |
1/7 |
|
у |
1 |
1/3 |
1/5 |
1/7 |
3 |
5 |
7 |
Построим данные точки на координатной плоскости хОу и соединим их.
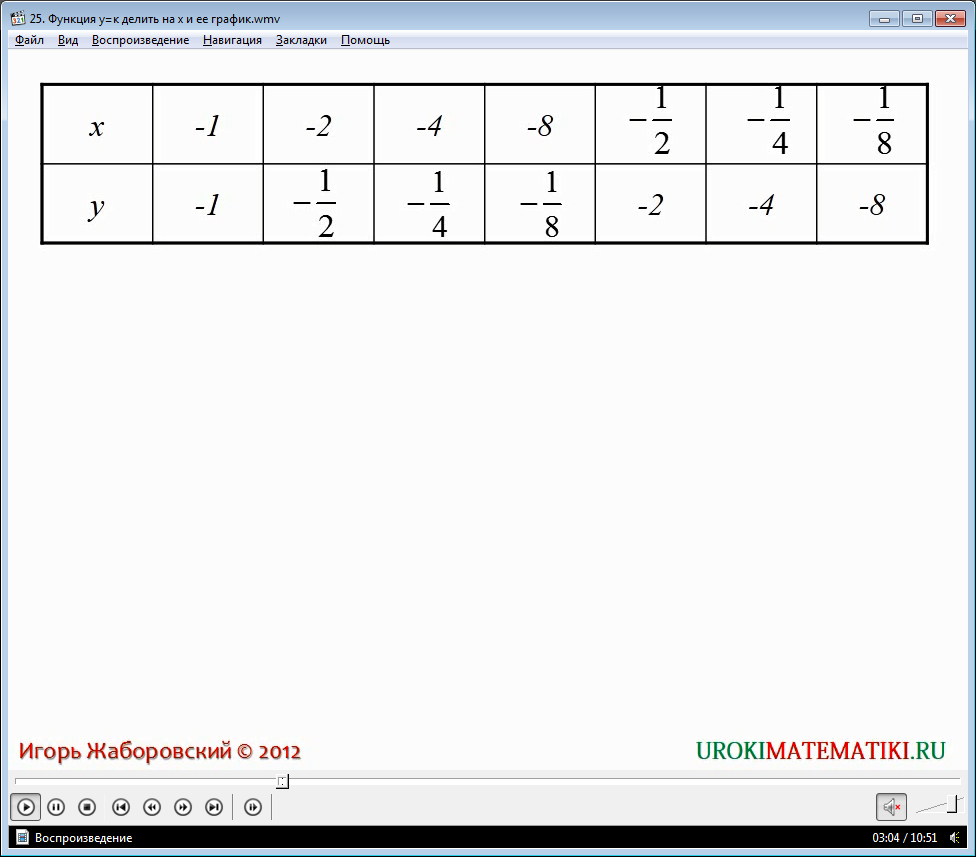
- В случае, когда х =1, то у = -1, х = -3, то у = -1/3; х = -5, то у = -1/5; х = -7, то у = -1/7.
И когда х = -1/3, то у = -3; х = -1/5, то у = 5; х = -1/7, то у = -7.
Составим таблицу:
|
х |
-1 |
-3 |
-5 |
-7 |
-1/3 |
-1/5 |
-1/7 |
|
у
|
-1 |
-1/3 |
-1/5 |
-1/7 |
-3 |
-5 |
-7 |
Построим данные точки на координатной плоскости хОу и соединим их.
Далее объедините два построенных графика в один. Полученный рисунок называется гиперболой, он и будет графиком заданной функции.
Пример с другими координатами и последовательность построения графика вы сможете увидеть в видео.
Также в видеоуроке вы ознакомитесь с основными геометрическими свойствами гиперболы.
- Гипербола, как и парабола, обладает симметрией. Если провести прямую через начало координат 0, то она пересечет гиперболу в двух точках, которые лежат на прямой на противоположных сторонах от точки 0 и на равных от неё расстояниях. Тем самым 0 будет являться центром симметрии гиперболы, и она будет симметрична относительно начала координат.
- Симметричные, относительно начала координат, части гиперболы называются её ветвями.
- Одна ветвь гиперболы расположена вблизи оси абсцисс, другая – вблизи ординат. В таких случаях соответствующие прямые принято называть асимптотами. Это значит, что гипербола имеет две асимптоты – ось х и ось у.
- Помимо центра симметрии гипербола имеет оси симметрии.
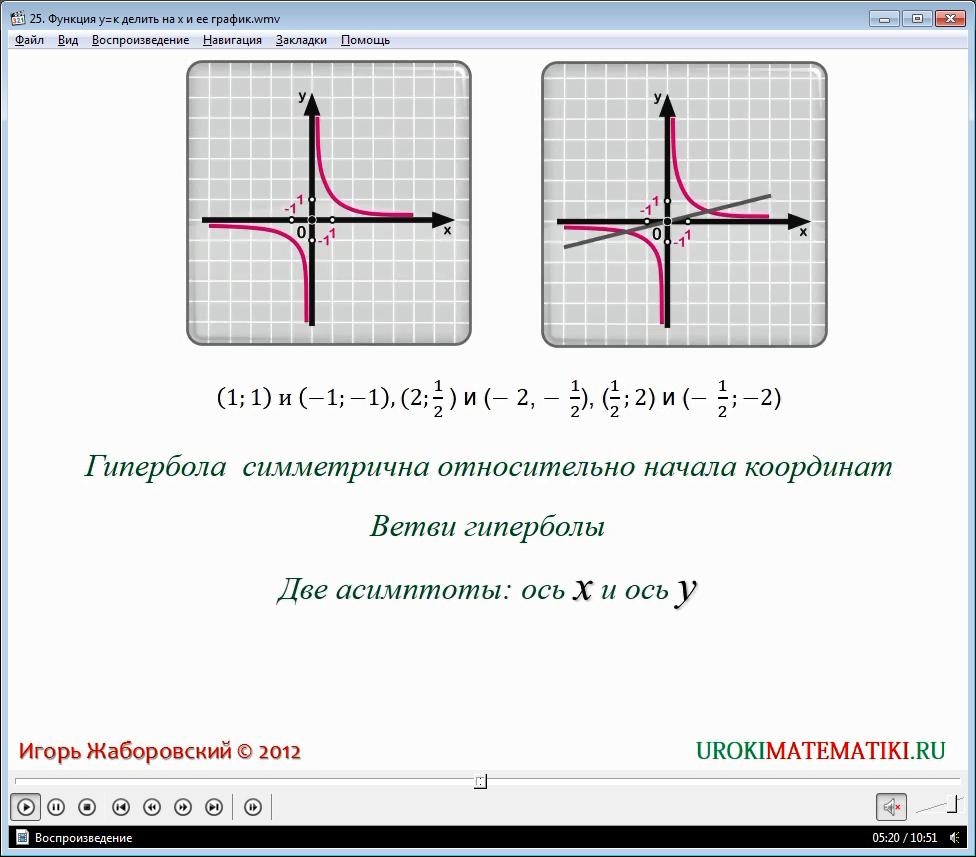
Графиком функции y = k/x, при k не равно 0 является гипербола, ветви которой находятся в 1 и 3 координатных плоскостях, в случае, когда k > 0, и во 2 и 4 k > 0, и во 2 и 4 координатных плоскостях, когда k < 0. (0,0) – точка центра симметрии гиперболы, а осями координат являются её асимптоты. Функцию y = k/x называют обратно пропорциональной, в силу того, что её величины – x и у, являются обратно пропорциональными, а число k - это коэффициент обратной пропорциональности.
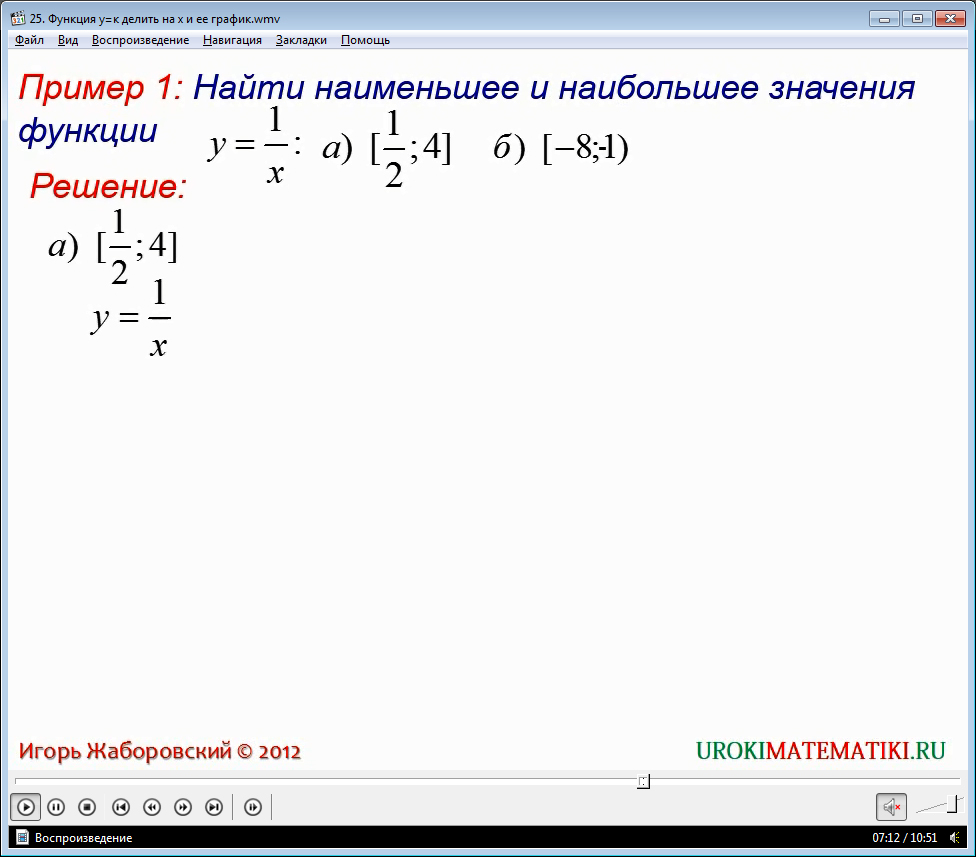
Примеры и более подробную информацию по теме вы можете получить при просмотре видеоурока.
| Автор | |
|---|---|
| Дата добавления | 30.07.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 8297 |
| Номер материала | 548 |