
Урок "Неравенство треугольника"

Краткое описание документа:
Видеоурок «Неравенство треугольника» раскрывает содержание и доказательство теоремы о неравенстве треугольника. Задача данного видеоурока – облегчить запоминание теоремы и следствия из нее, понимание и запоминание хода рассуждений при ее доказательстве.
Высокий уровень наглядности материала, голосовое сопровождение дает возможность использовать данное пособие в качестве самостоятельной части урока, освобождая время учителя для улучшения качества обучения, усиления индивидуальной работы с учениками.
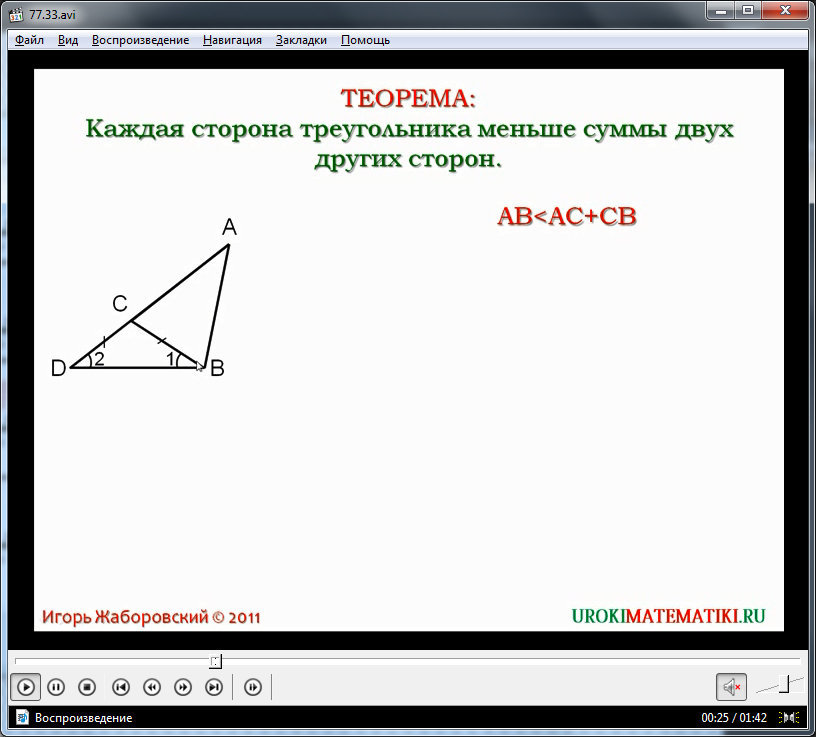
Видеоурок начинается с представления темы и формулировки теоремы о неравенстве треугольника. Для запоминания утверждения теоремы она выведена на экран и выделена цветом. Данная теорема утверждает, что любая сторона треугольника является меньшей суммы двух других его сторон. Доказательство утверждения предлагается рассмотреть на примере треугольника Δ, демонстрируемого под текстом теоремы на экране.
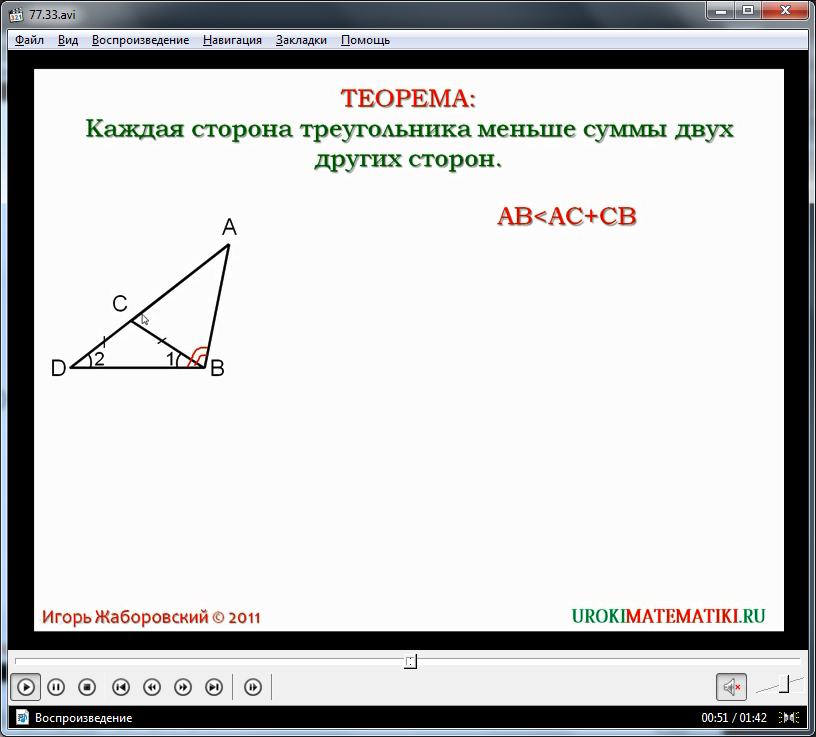
Уточняется, что для доказательства теоремы необходимо подтвердить, что сторона AB является меньше величины суммы сторон AC и CB. Данное утверждения обозначено на экране выражением AB<AC+CB. Чтобы доказать данное неравенство предлагается произвести дополнительное построение. На прямой, на которой лежит сторона AC откладывается отрезок длиной, равной CB. Образовавшийся при этом треугольник ΔDCB является равнобедренным по построению, поэтому его углы, противолежащие равным сторонам, будут равны. При этом в треугольнике ΔABD угол ∠ABD больше угла ∠1, так как угол ∠1 является его частью. Соответственно, ∠ABD больше и угла ∠2, так как ∠1=∠2. Зная, что напротив большего угла в треугольнике располагается большая сторона, отмечаем, что напротив ΔABD лежит сторона AD, большая, чем сторона AB. То есть AB<AD. При этом AD – это сумма сторон AB и CB. Данное равенство выведено на экран: AD= AC+CD=AC+CB. Исходя из данного равенства и построения, можно утверждать, что AB<AC+CB. Утверждение данной теоремы доказано.
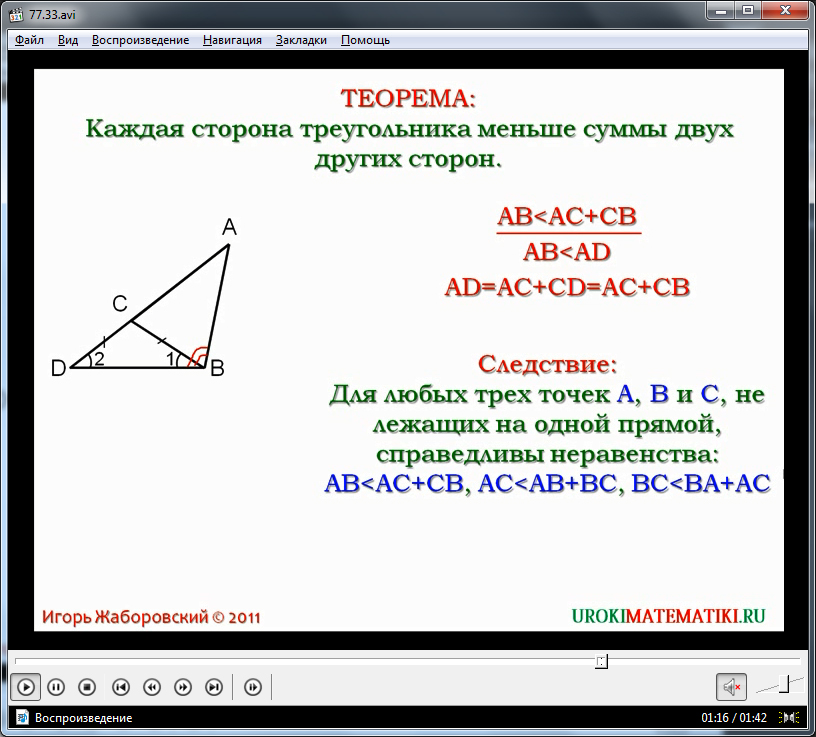
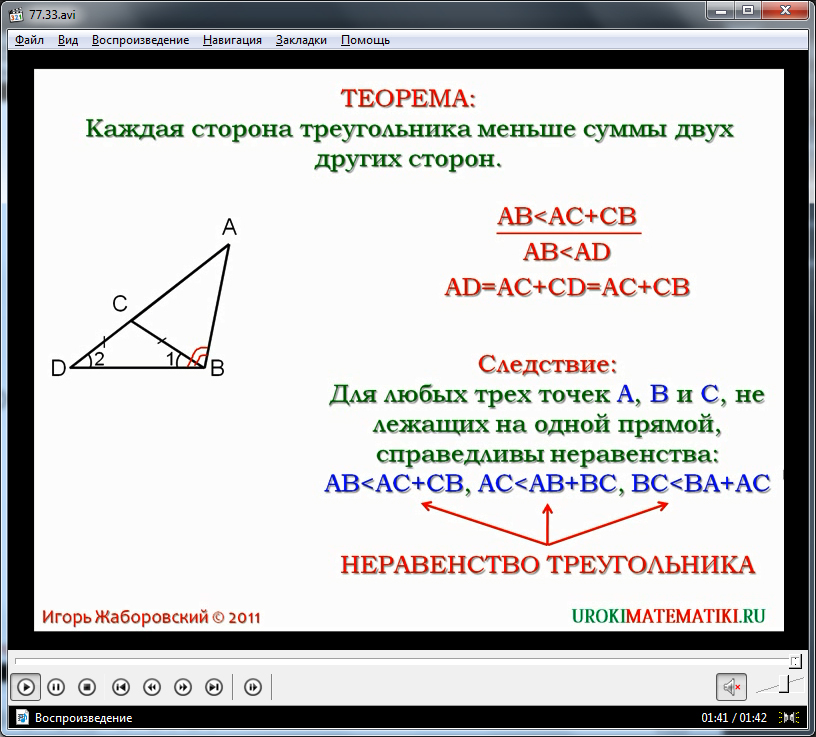
Освоив данную теорему, можно рассматривать ее следствие, утверждающее, что для любых трех точек A,B,C, которые не принадлежат одной прямой, справедливы неравенства: AB<AC+CB, AC<AB+BC, BC<BA+AC. Каждое из данных неравенств представляет собой неравенство треугольника. Данное понятие выделено на экране для запоминания учащимися.
Видеоурок «Неравенство треугольника» может быть использовано учителем на уроке геометрии в качестве наглядного пособия или как часть урока вместо объяснения учителем новой темы. Подробное понятное объяснение заменит учителя при самостоятельном изучении предмета учеником, а также поможет объяснить предмет при дистанционном обучении.
| Автор | |
|---|---|
| Дата добавления | 02.08.2014 |
| Раздел | Геометрия |
| Подраздел | Видеоурок |
| Просмотров | 8063 |
| Номер материала | 520 |