
Урок "Приближенные значения чисел. Округление чисел"

Краткое описание документа:
Видеоурок «Приближенные значения чисел. Округление чисел» - наглядное пособие для представления соответствующей темы урока. В ходе демонстрации ученики знакомятся с понятием приближенного значения, осваивают правила округления чисел. Учителю необходимо сформировать умение учеников округлять числа до указанного разряда. С помощью данного видеоурока это сделать значительно проще. С помощью анимационных эффектов, ярких иллюстрированных примеров подробно и понятно объясняется суть процесса округления, вводятся его правила. Данные приемы помогают ученикам быстрее запомнить материал, глубже его понять. Данное видео повышает эффективность обучения, способствует быстрому достижению целей урока.

Видеоурок начинается с представления названия темы и иллюстрированного примера приближенного значения. На рисунке изображены весы с тыквой. В первой части рисунка на чаше весов располагаются гири 2 кг и 1 кг, и видно, что этого веса недостаточно для уравновешивания весов. На вторых весах тыква уравновешивается двумя гирями по 2 кг. Видно, что этот вес превышает нужную величину. Из данных взвешиваний ясно, что масса тыквы более 3 кг, но менее 4 кг. Отмечается, что в математической записи это будет 3<x<4. Если же говорит о приближенном значении веса, то 3 является приближенным значением х с недостатком, а 4 – приближенным значением х с избытком. Данные определения приближенных значений выводятся на экран для запоминания.
Приводится еще пример приближенных значений числа. На экран выводится изображение отрезка АВ, длина которого составляет у. Рядом с отрезком расположили линейку, по которой можно определить, что длина отрезка больше 6 единиц, но меньше 7. Согласно уже известным данным о характере приближенных значений, можно утверждать, что 6 – это значение длины данного отрезка с недостатком, при этом 7 – приближенное значение числа с избытком. Имеющиеся сведения о значении у свидетельствуют о том, что длину можно оценить с помощью неравенства 6<y<7. Аналогичные выражения a<х<b для оценки некоторого значения х определяют приближенное значение а числа х с недостатком и приближенное значение b числа х с избытком. К тому же, по рисунку можно определить, что длина отрезка АВ ближе к 6 см, чем к 7, поэтому можно уверенно говорить, что приближенное значение длины отрезка – 6 см. также отмечается, что иначе говорят об этом – число 6 получается при округлении длины отрезка до целых.
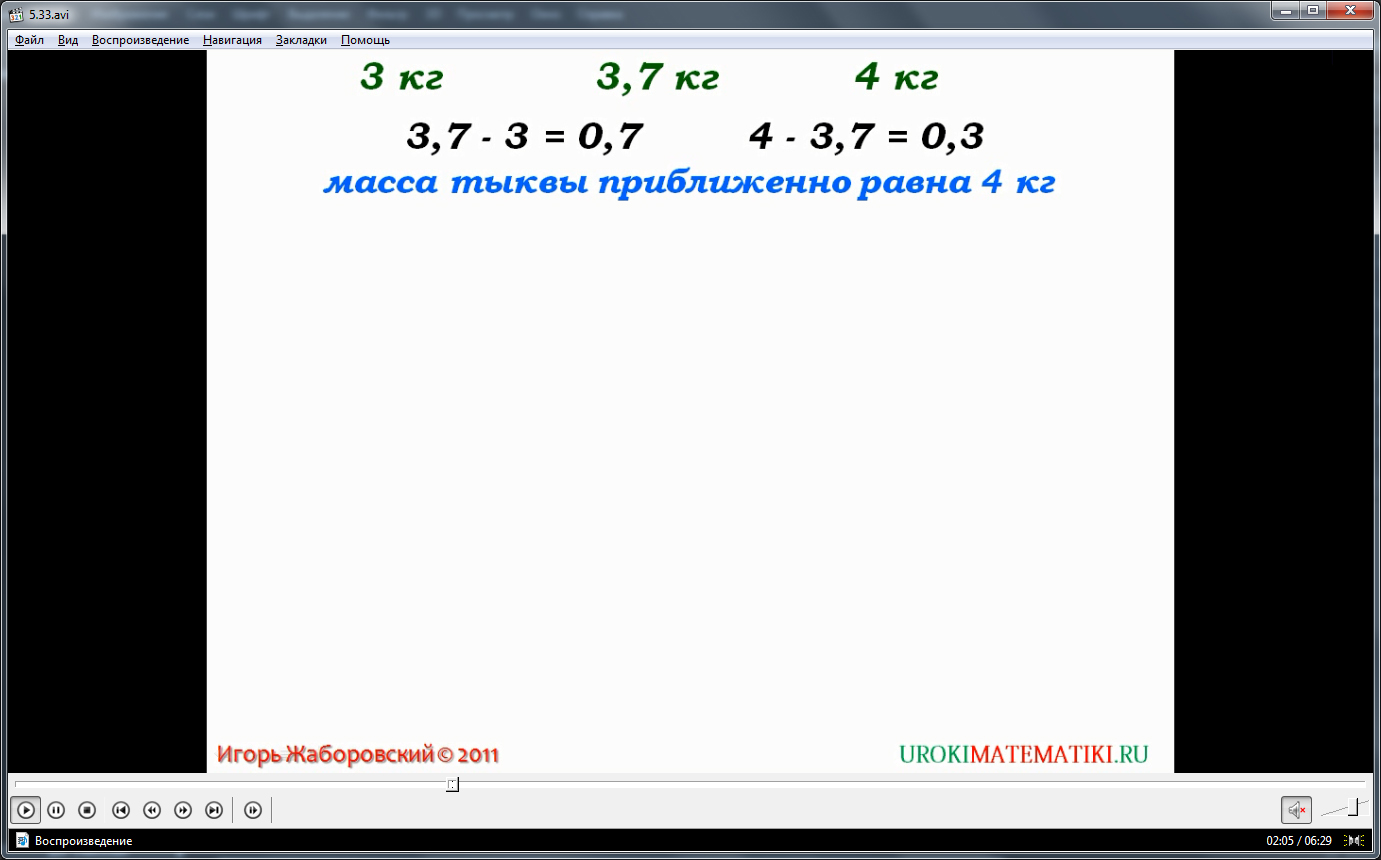
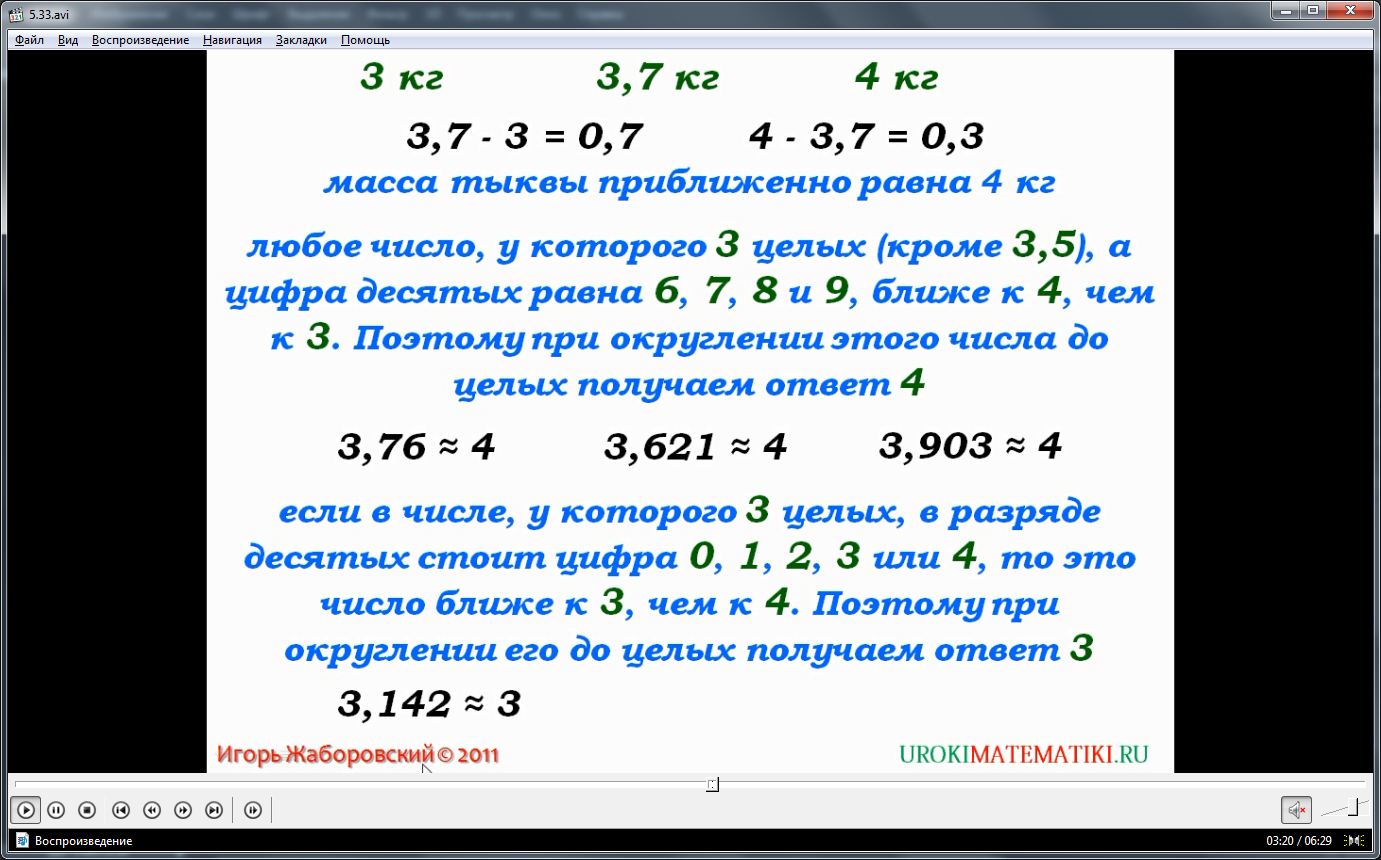
Округление чисел рассматривается более подробно. Для этого предлагается рассмотреть величину 3,7 кг и ее приближенные значения 3 кг и 4 кг. Чтобы оценить, к какому числу ближе данное значение, находят разность между числом и его приближенным значением. Очевидно, что разница между 3 кг и 3,7 кг будет 0,7, а между 3,7 кг и 4 кг разница 0,3. Так как разница между числом 3,7 и 4 кг меньше, чем между 3,7 и 3, то приближенное значение 3,7 кг будет 4 кг. Для этого примера также указано, что всякое число, имеющее 3 целых и десятых 6,7,8,9 будет ближе к 4, чем к 3, поэтому его приближенное значение равно 4. Приводится пример такого числа – 3,76. Приближенное значение 4, так как в десятых у этого числа цифра 7. Аналогично оценивается 3,621 и 3,903. Приближенным значением этих чисел также будет число 4, так как в первом случае десятые доли представляет число 6, а во втором случае – число 9. Также представляется знак приближенного значения – двойная волнистая линия.
Далее рассматривается случай, когда десятые представлены цифрами из числа 0,1,2,3,4, данное число будет ближе к 3, а не к 4, поэтому округлив такое число, получается число 3. К данному правилу приводятся примеры 3,142, 3,498, 3,074. В них отмечается особенность – десятые представлены цифрами 1, 4, 0. Отмечается, что это определяет их приближенное значение – 3.
Отдельно рассматривается случай, когда десятые представлены цифрой 5. В этом случае, если число одинаково отдалено от приближенного значения по недостатку и по избытку: 3,5-3=0,5 и 4-3,5=0,5. Чтобы вопросов не возникало с решением такого задания, условились считать приближенным значением – по избытку. Поэтому округленное значение числа равно 4.
Далее следуют общие правила округления чисел до определенного разряда. Говорится о том, что операция замены дробного или смешанного значения натуральным числом, а также нулем, является округлением до целых данного числа. Также может быть произведено округление до любого разряда. Ниже приводится замечание, что округляя до определенного разряда, последующие разряды обнуляют, а эти нули можно отбросить.
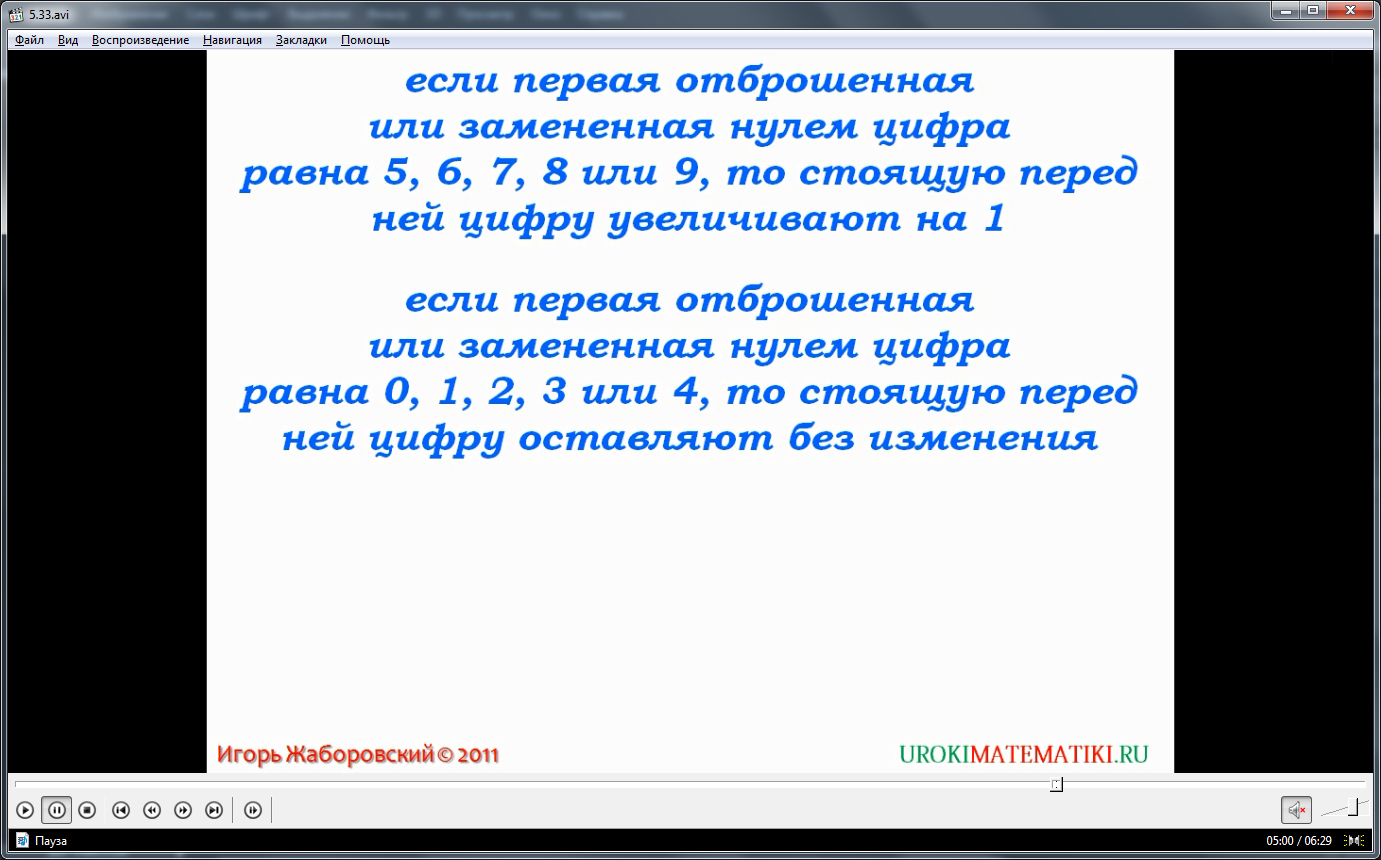
Обобщая рассмотренные особенности округления, формулируются правила округления чисел до определенного разряда. Отмечается, что если первая обнуленная цифра равняется 5,6,7,8,9, то предыдущий разряд увеличивает значение на 1, а если первая цифра, отброшенная в результате округления, 0,1,2,3,4, тогда цифра предыдущего разряда остается неизменной. Приводятся примеры округления чисел. Округляя число 86,2759 до десятых, отмечается, что следующий разряд содержит цифру 7, поэтому в десятых проставляется цифра, на 1 больше – 3. Приближенное значение числа – 86,3. Округляя до разряда стотысячных число 6723401, замечается, что после этого разряда цифра 2, значит, цифра 7 разряда стотысячных остается неизменной. Приближенное значение числа получилось 6700000 или 6,7 млн.
Демонстрация заканчивается вопросами, на которые нужно ответить ученикам, чтобы учитель мог понять, как понят материал. Им необходимо вспомнить, какое число называется приближенным с недостатком, какое – приближенным значением с избытком, что означает округление до целых. Нужно сформулировать правило округления и сориентироваться, как поступать при округлении до определенного разряда, когда следующая за ним цифра – 8, 5, 3.
Видеоурок «Приближенные значения чисел. Округление чисел» рекомендуется применять на традиционном школьном занятии для повышения его эффективности. Также материал полезен для обеспечения наглядности при проведении дистанционного занятия по данной теме. Видео может быть рекомендовано ученикам, самостоятельно осваивающим учебный материал.
| Автор | |
|---|---|
| Дата добавления | 28.07.2014 |
| Раздел | Математика |
| Подраздел | Видеоурок |
| Просмотров | 7470 |
| Номер материала | 393 |