
Урок "Проценты"

Краткое описание документа:
Видеоурок «Проценты» - наглядное пособие для изучения соответствующей темы урока. В ходе демонстрации ученики с помощью практических заданий подводятся к необходимости изучения данного понятия. Формируется представление о проценте и связи этого понятия с частью некоторой величины, умение решать задачи различного типа, в которых используется понятие процентов. Видео может использоваться как наглядное пособие, сопровождая объяснение учителя ярким наглядным материалом, а также применяться в качестве отдельной части урока, заменяющей объяснение учителя по данной теме.
Видеоурок – эффективный инструмент учителя для достижения целей обучения на уроке математики. Этому способствуют приемы, применяемые в ходе демонстрации видео. Определения и правила выводятся на экран в текстовом виде, выделяются разными шрифтами и озвучиваются для лучшего их запоминания. Лучшему пониманию условия задачи и ее решения способствуют иллюстрации, вставка анимационных эффектов. А также благодаря анимационным эффектам, помогающим в последовательной подаче материала, и голосовому сопровождению, пособие может полностью заменить объяснение учителя.

Видеоурок начинается с представления названия темы. Понятие процента вводится с необходимости вычисления сотой доли некоторых физических величин. Ученикам представляются уже знакомые им соотношения центнера и килограмма, метра и сантиметра, гектара и ара. Данные соотношения выводятся на экран Видеоурок «Проценты» 0,01 ц=1 кг, 0,01 м=1см, 0,01 га=1 ар. Отмечается, что данные выражения можно читать как «1 кг – сотая часть центнера», «1 сантиметр – сотая часть метра», «1 ар – сотая часть гектара». При этом сотая часть иначе называется в математике 1 процентом числа. Поэтому в рассматриваемых выражениях вводится понятие процента центнера, а также процента метра и процента гектара.
Математическое понятие «процент» определяется как сотая часть. Определение выделено на экране цветным жирным шрифтом для запоминания. Также вводится обозначение математического понятия процента %, объясняется корректное использование термина в математическом языке. Для этого на экране даются математические выражения, которые могут быть частью задачи и озвучивается правильное использование термина при формулировке условия задачи. Представлено два таких выражения. Ниже делается замечание, что, с учетом представления о проценте как сотой части некоторой величины, вся величина составляет 100%.
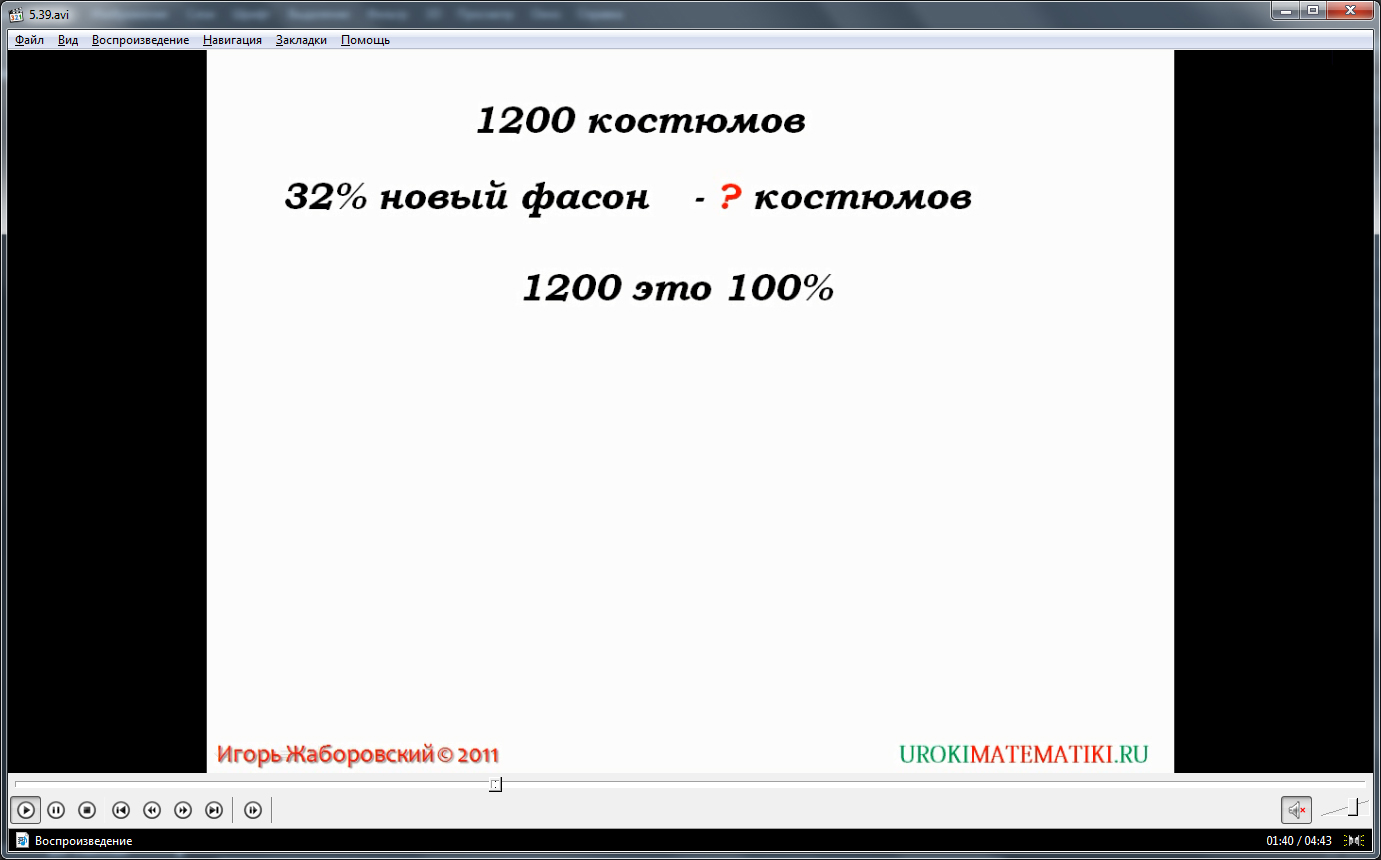
Далее рассматривается решение задачи, где необходимо найти некоторый процент от известного числа. В задаче указано, что швейная фабрика пошила 1200 костюмов. В их числе 32% составили новый фасон. Необходимо найти количество костюмов нового фасона. Для решения задачи предлагается сначала найти 1% всего числа выпущенных костюмов. Для этого все число делят на 100%, то есть 1200:100=12. Найденное значение означает, что в 1% выпуска содержится 12 костюмов. Для нахождения 32% выпуска, следует умножить количество костюмов в 1% на число процентов, вычисляя 12·32=384. Полученное число 384 дает количество костюмов нового фасона в выпуске швейной фабрики.
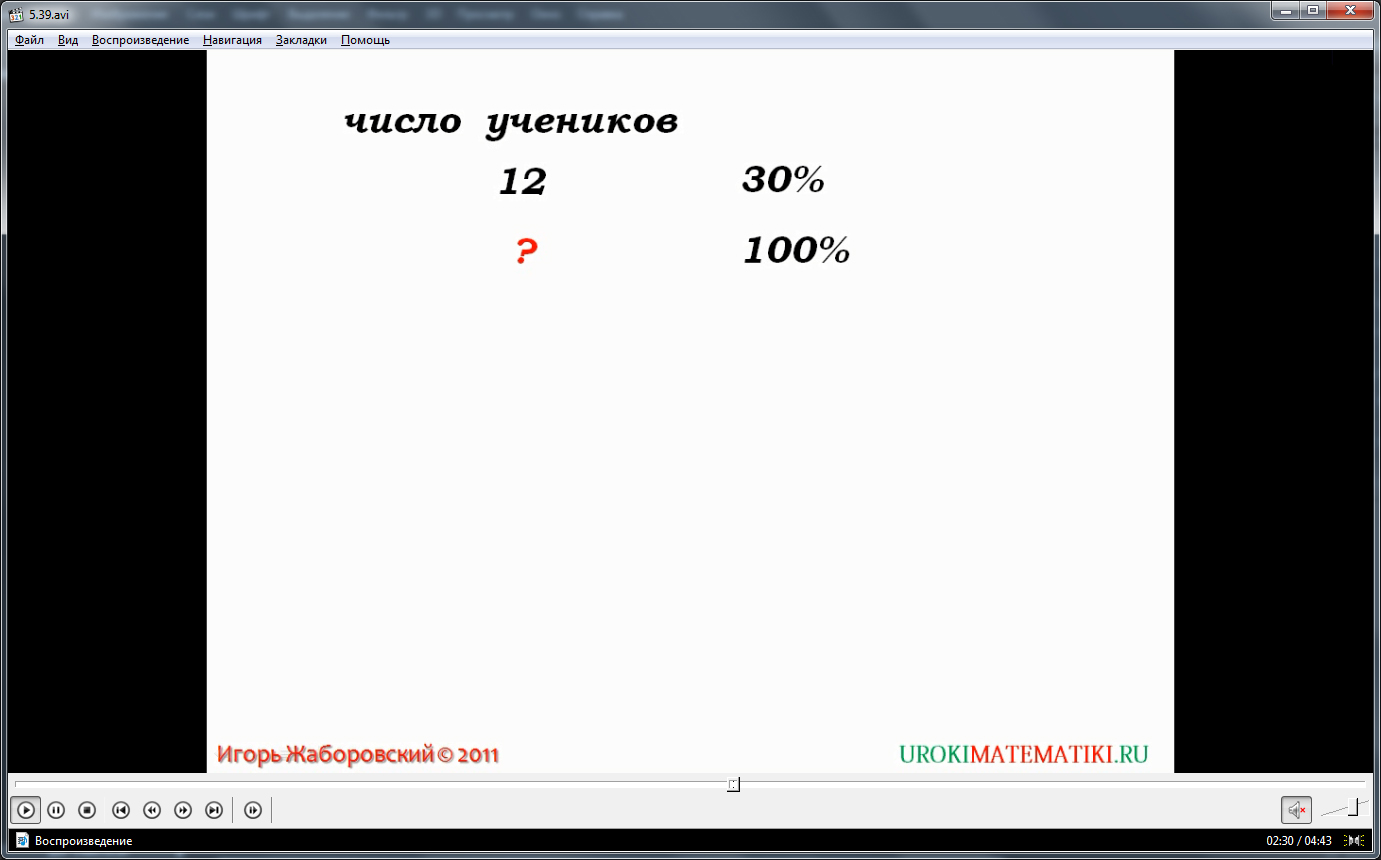
Вторая рассмотренная задача описывает другой тип задач с процентами – нахождение общего числа, зная некоторое число процентов. В задаче сказано, что оценку «отлично» получили 30% учеников – это 12 учеников. Нужно найти, сколько всего учеников в классе. Для решения задачи данного типа, предлагается сначала найти, сколько учеников представлено в 1%. Зная, что 12 учеников – это 30%, то 1% составляют 12:30=0,4. Зная, сколько содержит 1%, находим все число, умножив это значение на 100%, то есть 0,4·100=40. Так мы определили, сколько учеников в классе.
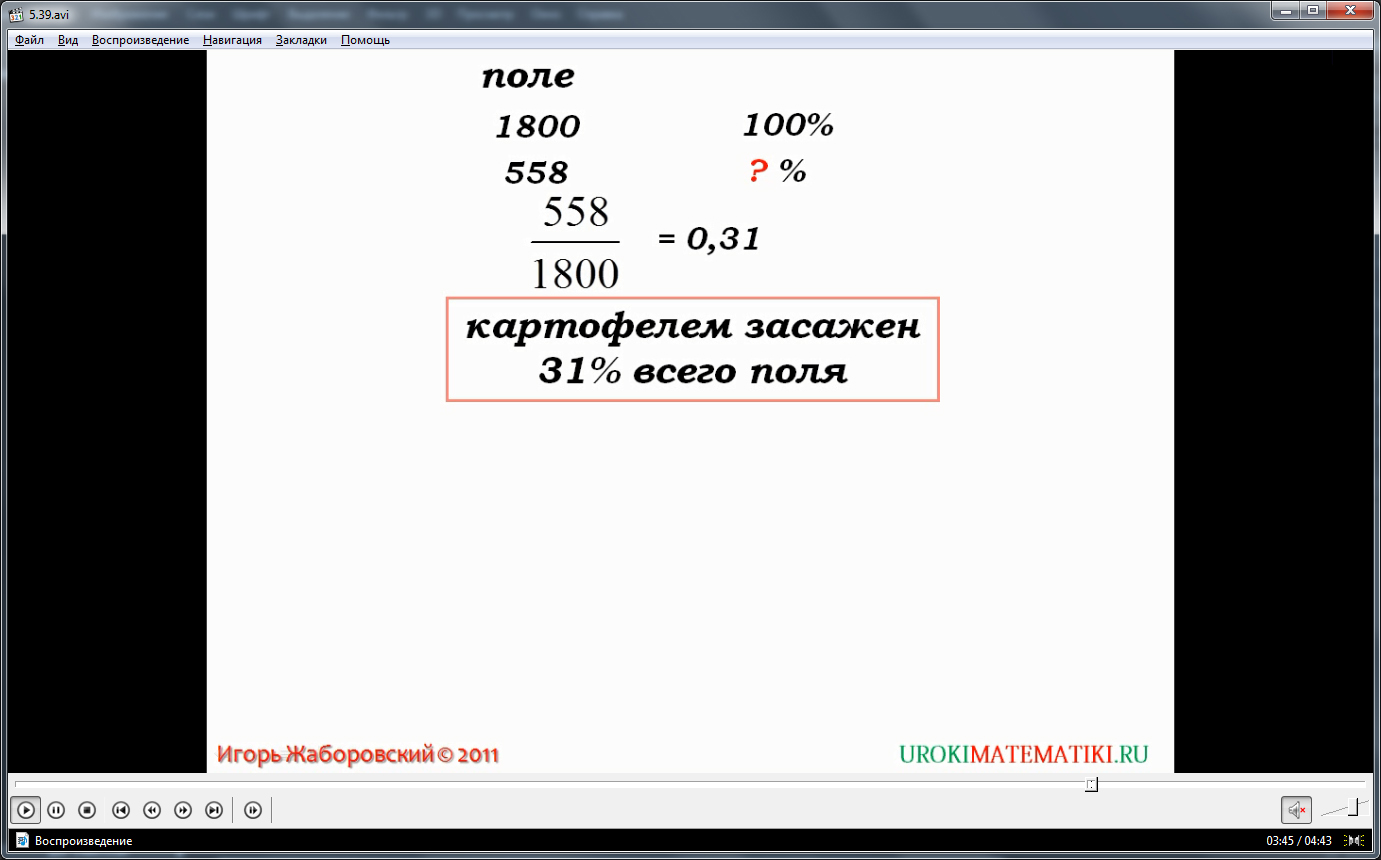
В ходе решения третьей задачи использован подход, который формирует понятие о связи процента с долей числа. Условие задачи - поле площадью 1800 гектаров, которое засеяно картофелем на 558 гектарах. Необходимо определить, какой процент поля засеян картофелем. Для этого предлагается найти долю засаженного участка в общей площади поля, представленную дробью 558/1800. Зная, что знак дроби представляет собой деление, находим значение данной дроби в десятичной записи 558/1800=0,31. Помня о том, что процент – это сотая часть величины, отмечаем, что 0,31=31%. Это и есть ответ на вопрос – поле засажено картофелем на 31%.
Описанное решение задачи подводит к вопросу обращения десятичной дроби в проценты. Правило такого обращения выведено на экран и предложено к запоминанию. В нем указано, что для обращения десятичной дроби в проценты, ее необходимо умножить на 100. Обратной операцией производится обращение процентов в десятичную дробь – число процентов нужно разделить на 100. Для усвоения полученной информации описывается решение примеров. Чтобы обратить в число процентов дробь 0,971, нужно умножить ее на 100%, то есть 0,971·100%=97,1%. Значит, часть 0,971 означает 97,1%. Во втором примере необходимо обратить 39% в десятичную дробь. Для этого количество процентов делится на 100%, то есть 39%=39:100=0,39. Значит, 39% означает 0,39 часть некоторой величины.
В конце видеоурока ученикам предлагается ответить на вопросы, чтобы проверить насколько хорошо они усвоили изучаемый материал. Им необходимо вспомнить, что называют процентом, что представляет собой 1% физических величин – центнера, метра, гектара, правило обращения десятичной дроби в проценты и решение обратной задачи.
Видеоурок «Проценты» рекомендуется использовать для повышения эффективности урока математики на традиционных занятиях в школе. Также наглядный материал может быть полезен учителю, который проводит дистанционное обучение. Если ученик недостаточно хорошо освоил материал на уроке или осваивает тему самостоятельно, подробное понятное объяснение в данном пособии поможет ему научиться решать задачи на проценты, даст необходимую теоретическую базу для владения предметом.
| Автор | |
|---|---|
| Дата добавления | 29.07.2014 |
| Раздел | Математика |
| Подраздел | Видеоурок |
| Просмотров | 12703 |
| Номер материала | 398 |