
Урок "Среднее арифметическое"

Краткое описание документа:
Видеоурок «Среднее арифметическое» - наглядный материал, который применяется для проведения урока математики по данной теме в 5 классе. В ходе видеоурока формируется представление о среднем арифметическом, о необходимости находить данную величину при решении практических задач, умение вычислять среднее арифметическое нескольких чисел. Пособие может сопровождать объяснение учителя, обеспечивая его наглядность. Также материал может применяться вместо объяснения учителя, освобождая время преподавателя для проведения индивидуальной работы.
В видеоуроке используется иллюстрированный видеоматериал, с помощью которого формируется глубокое понимание изучаемого понятия, демонстрируется прикладное значение изучаемого математического аппарата. Анимационные эффекты акцентируют внимание на изучаемом материале, удерживания внимание учеников на обучении. С помощью анимационных эффектов материал подается последовательно, выделяются важные понятия и особенности при описании решения примеров. Озвучивание видео дает возможность вставить важные комментарии, помогающие освоить учебный материал.
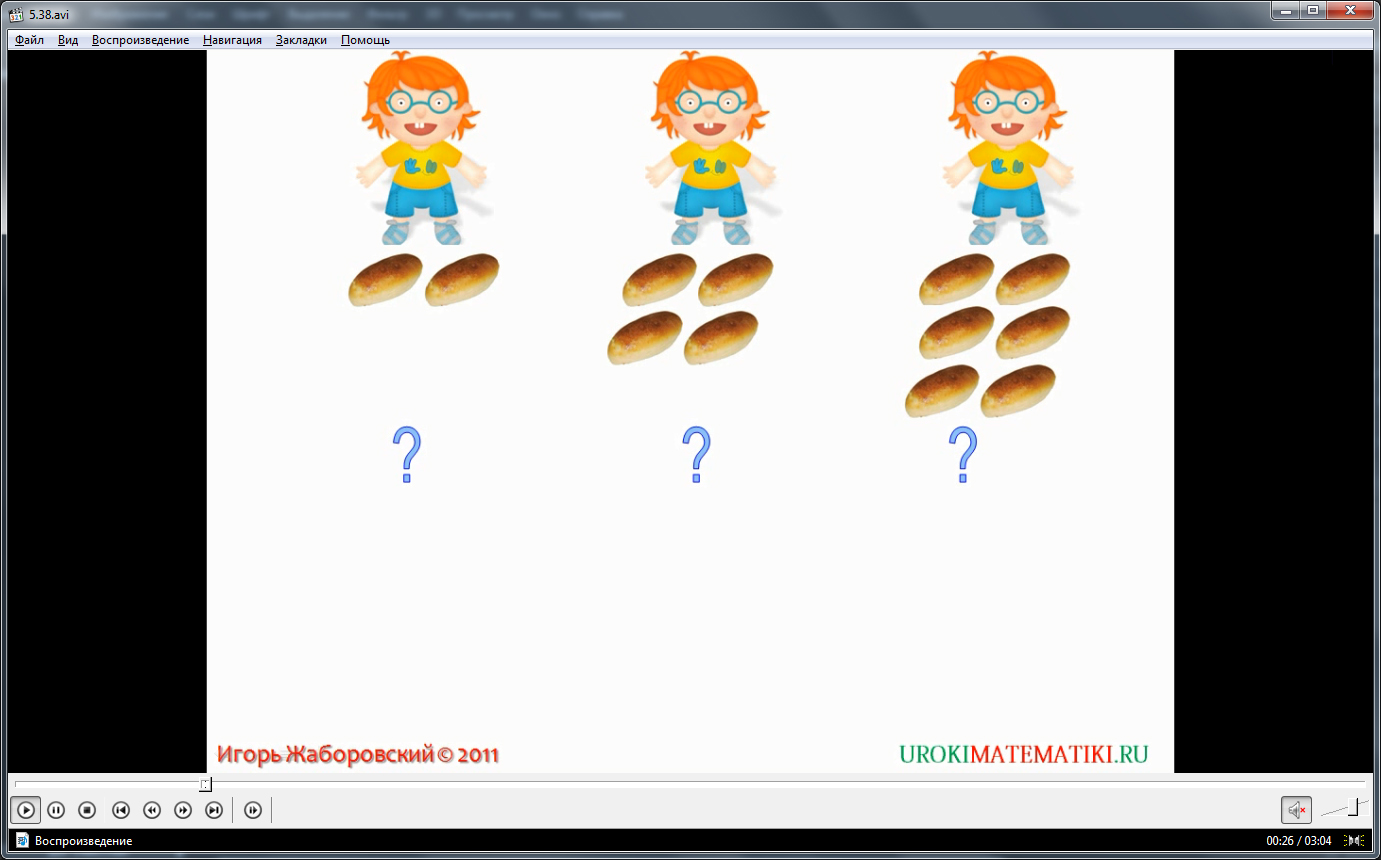
Видео начинается с демонстрации названия темы урока. Затем представляется задача, которая подводит к понятию среднего арифметического. В задаче следующее условие. Есть три мальчика, которые после похода становятся на привал. У первого мальчика есть 2 пирожка, у второго – 4, а у третьего -6. Им необходимо поделить эти пирожки поровну. Чтобы поделить имеющиеся пирожки поровну, мальчикам необходимо их сложить, а затем поделить на три человека. Для этого складываются 2+4+6=12 пирожков, которых всего было у мальчиков. Если пирожки поделить поровну на троих ребят, то получится по 12:3=4 пирожка. Иначе говоря, было найдено среднее арифметическое чисел 2, 4 и 6, которое равно 4.
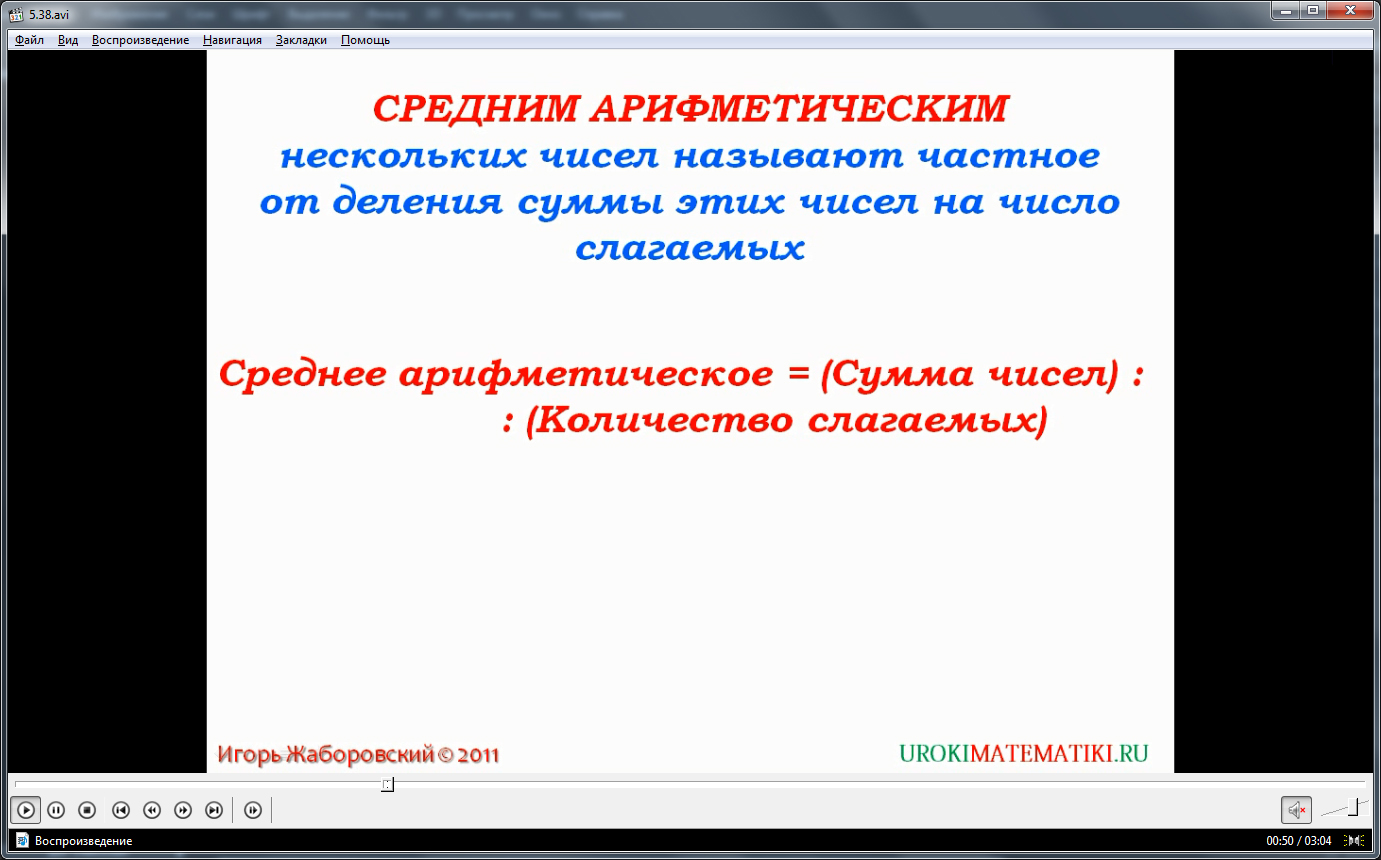
Далее представляется определение среднего арифметического нескольких чисел. В определении указано, что средним арифметическим называется частное от деления суммы нескольких чисел на их количество. Формула вычисления среднего арифметического определяется как частное от деления суммы чисел на их число. Определение и формула выделены цветным шрифтом и рекомендованы к запоминанию.
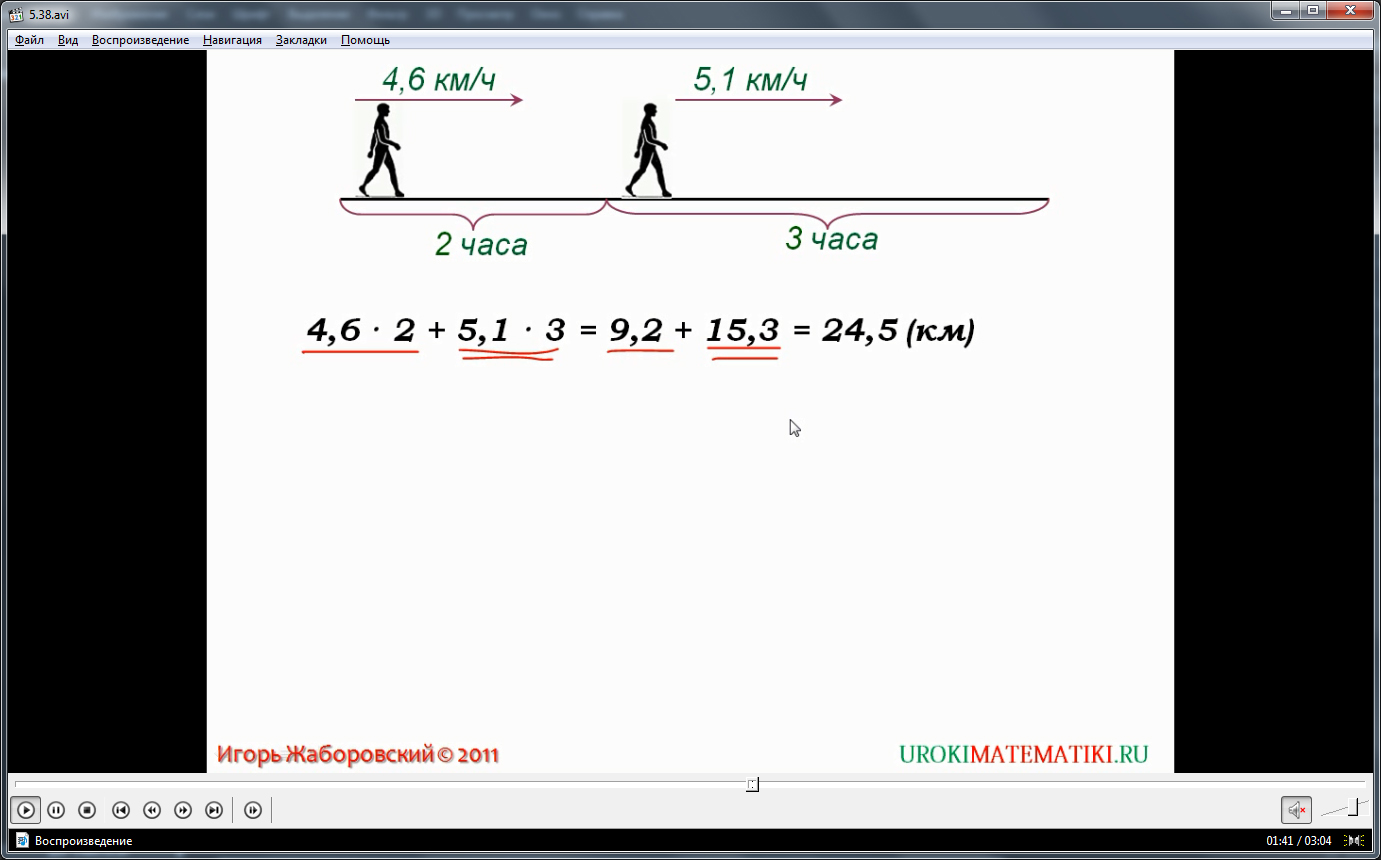
Примером задачи на нахождение среднего арифметического служит задача, представленная после формулировки. Дается иллюстрированное условие задачи. В нем указано, что человек проходит некоторый путь со скоростью 4,6 км/ч в течение 2 часов, а затем путь со скоростью 5,1 км/ч в течение 3 часов. Необходимо найти среднюю скорость, с которой идет человек. Чтобы найти эту скорость, нужно найти весь путь, который проходит человек. Согласно формуле для нахождения значения пути, его значение определяется произведением скорости на время, за которое путь пройден. Общее значение пути находится выражением 4,6·2+5,1·3=9,2+15,3=24,5 км. Чтобы найти среднее значение скорости, нужно путь разделить на время, за которое этот путь преодолен. Для этого 24,5 км делят на 5 часов, получив 24,5:5=4,9 км/ч. Данный результат представляет среднюю скорость движения человека. Это понятие выделяется отдельно, подчеркивая важное прикладное значение изученного термина. Дается формулировка средней скорости как результата от деления всего пути, пройденного человеком, на время, которое затрачено на этот путь. Также отмечается, что это среднее арифметическое скоростей за данный промежуток времени.
Кроме нахождения средней скорости, отмечается приложение среднего арифметического в вычислении средней урожайности, средней производительности и других величин, необходимых для оценки деятельности человека.
В конце видеоурока представлены вопросы, на которые необходимо ответить ученикам, чтобы продемонстрировать понимание изученного материала. Им необходимо будет сформулировать определение среднего арифметического нескольких чисел, правило его отыскания, объяснить, как находится средняя скорость движения.

Видеоурок «Среднее арифметическое» предназначен для применения на школьном уроке математики для повышения эффективности обучения. Данное наглядное пособие поможет быстрее достичь целей урока учителю, который проводит дистанционное обучение. Материал может быть предложен для освоения ученику, который недостаточно хорошо усвоил тему на уроке в школе или самостоятельно изучает предмет.
| Автор | |
|---|---|
| Дата добавления | 29.07.2014 |
| Раздел | Математика |
| Подраздел | Видеоурок |
| Просмотров | 6355 |
| Номер материала | 397 |