
Урок "Деление на десятичную дробь"

Краткое описание документа:
Видеоурок «Деление на десятичную дробь» - наглядный материал для проведения урока математики по данной теме. В ходе демонстрации вводятся правила деления десятичных дробей, их особенности. Теоретический материал подкрепляется примерами, которые подробно и понятно описывают решение подобных задач. В ходе видеоурока формируется представление о правилах выполнения действий над десятичными числами, практической ценности данного математического аппарата, умение производить эти действия. Видео может сопровождать объяснение учителя. Также видеоматериал может использоваться как самостоятельная часть урока, полностью заменяя объяснение учителя.
Чтобы повысить эффект применения данного обучающего инструмента, используется много эффективных приемов. Запомнить теоретический материал помогает представление правил в текстовом виде на экране, цветным шрифтом, а также дополнительное озвучивание, вставка важных комментариев диктора. С помощью анимационных эффектов материал подается последовательно, акцентируя внимание ученика на важных деталях, которые помогают глубже понять механизм выполнения действий.
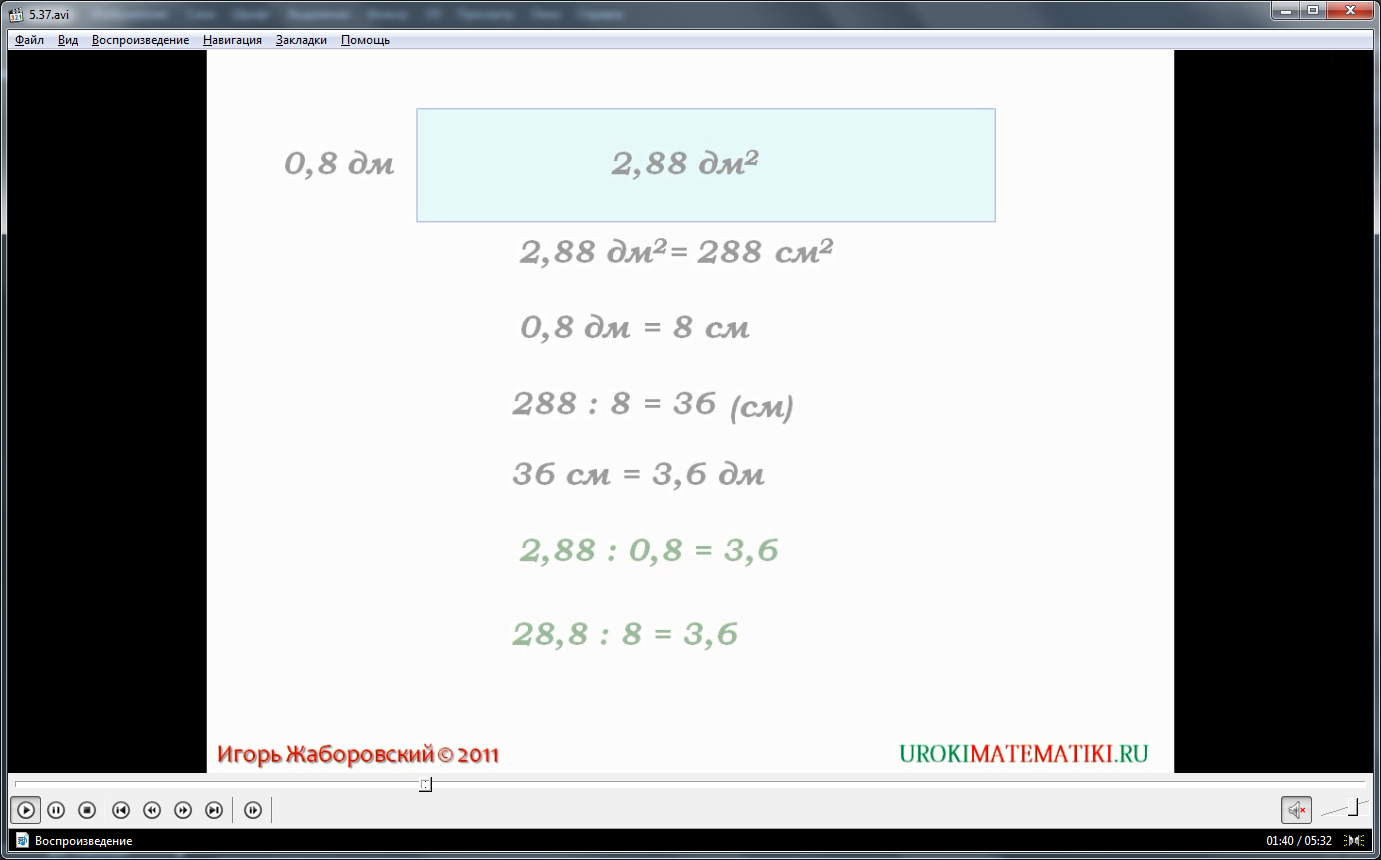
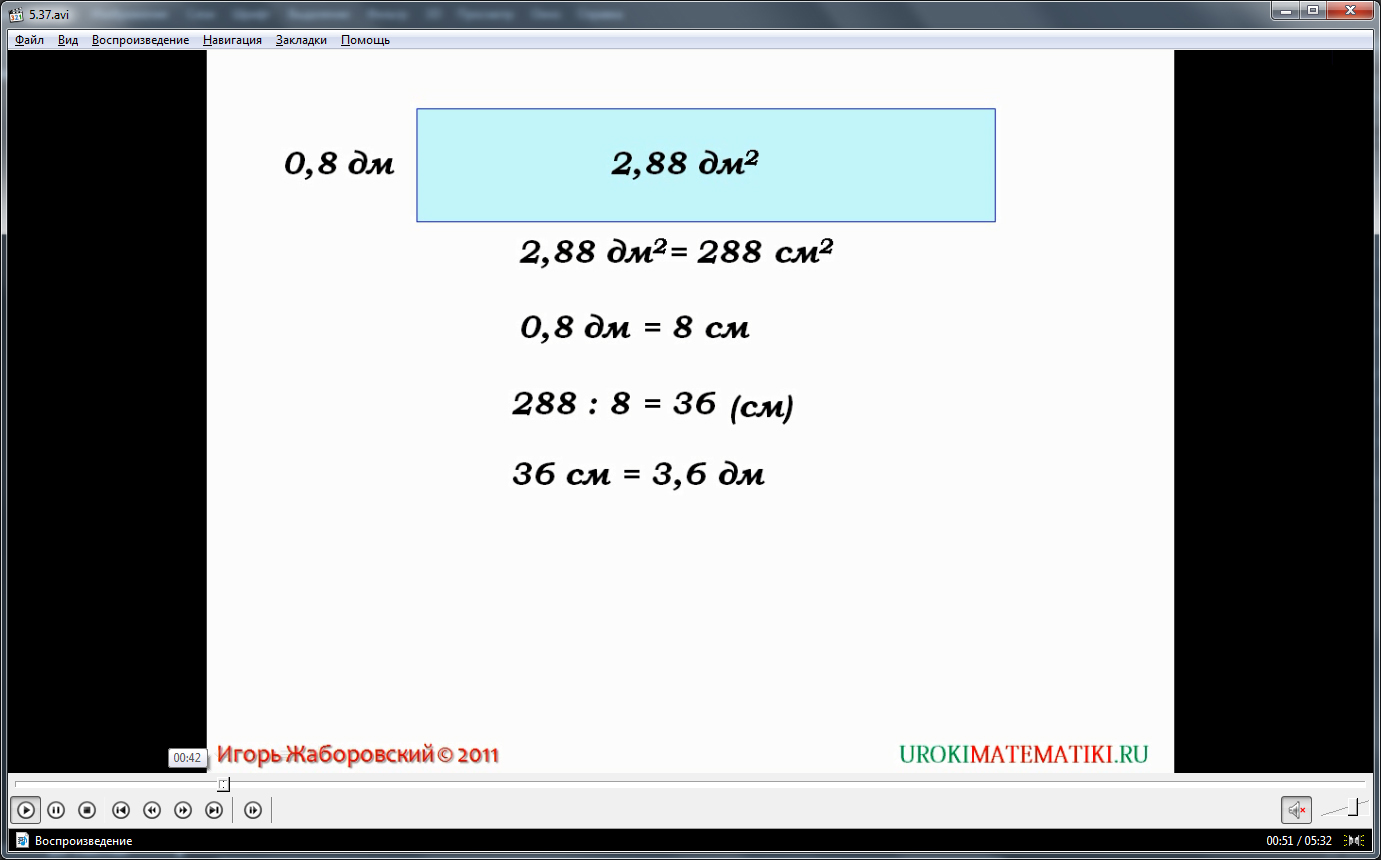
Демонстрация начинается с представления названия темы. Затем представлено решение задачи, для решения которой необходимо произвести действия по вычислению частного двух десятичных дробей. На экране изображается прямоугольник, о котором известно, что его площадь 2,88 кв.дм, а ширина прямоугольника 0,8 д. Необходимо определить вторую сторону – длину прямоугольника. Для этого сначала выполняются действия в сантиметрах. Площадь прямоугольника представляется в квадратных сантиметрах 2,88 кв.дм.=288 кв.см. Также преобразуется ширина 0,8 дм=8 см. чтобы найти вторую сторону прямоугольника, находят частное 288:8=36 см. представляем частное в дециметрах 36см=3,6 дм. Это означает, что при делении дробей, представляющих параметры в дециметрах, мы получаем 2,88:0,8=3,6.
Рассмотренным примером ученики подводятся к пониманию общего порядка деления некоторого числа на десятичную дробь. Данное правило представляется на экране. В нем указано, что для нахождения частного от деления на десятичную дробь необходимо перенести запятую правее на столько разрядов, сколько их насчитывается в делителе после запятой. Затем выполняются действия над натуральными числами.
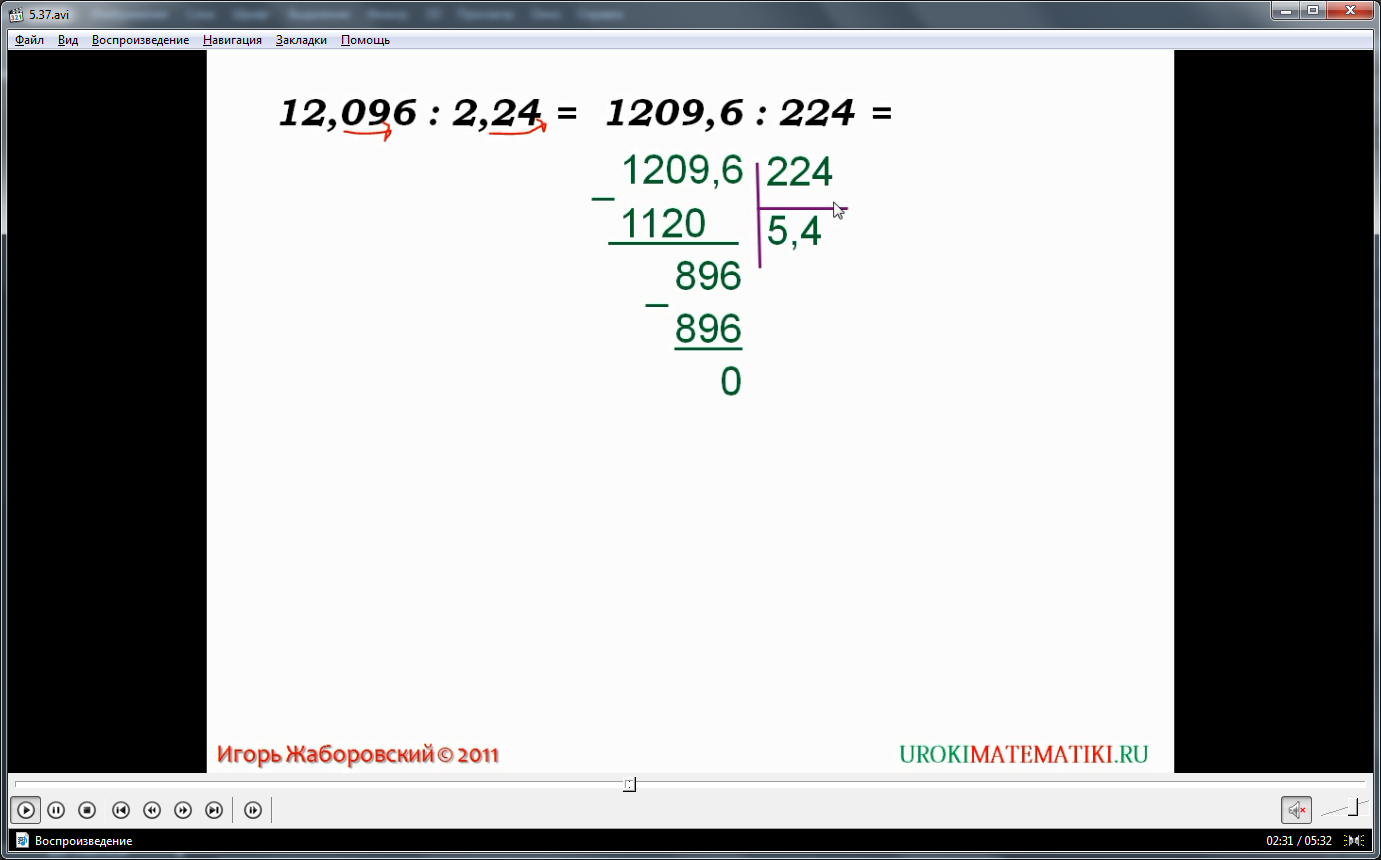
Изученное правило подкрепляется примерами, которые помогают усвоить материал. Рассматривается решение выражения 12,096:2,24. С помощью анимации ученикам подробно объясняется, как переносится запятая на столько знаков, сколько в разрядах у делителя после запятой. В данном случае это два разряда. После переноса получается выражение 1209,6:224. Вычисляется данное выражение ниже в столбик. При вычислении обращается внимание учеников, когда ставится запятая при окончании целой части делимого. В результате вычисления получается значение 5,4. Аналогично вычисляется значение выражения 4,5:0,125. Сначала делимое с делителем преобразуются, изменив положение запятой. Она переносится на три знака вправо. В недостающие разряды вписываются нули.
Также ниже выводится правило, с помощью которого можно оценить корректность вычислений. В нем отмечается, что при делении на правильную дробь значение частного будет превосходить значение делимого, а при делении на неправильную дробь значение частного будет меньше значения делимого. Для описанных выше примеров это правило выражается в соотношениях 12,096>5,4 и 4,5<36. Эти соотношения отображают, что результатом деления на 2,24 стало число, меньшее делимого 12,096, а результатом деления на 0,125 стало число, большее делимого 4,5.
В следующем разделе видеоурока описывается деление на 0,1, 0,01 и др. Сначала приводится пример 2,467:0,01. Согласно изученному правилу, выполняем перенос запятой правее на 2 знака, получая выражение 246,7:1, что дает в результате 246,7. Из представленного примера видно, что аналогичные действия над десятичными дробями приводят только к переносу запятой. Ниже примера представляется правило, выделенное цветным шрифтом для запоминания. В нем указано, что для нахождения частного от деления на 0,1, 0,01 и др., необходимо переставить запятую правее на то количество знаков, сколько насчитывается после запятой в делителе. Это действие тождественно умножению данного числа на 10, 100 и др. Также акцентируется внимание на важной особенности выполнения таких действий – если цифр для переставления запятой недостаточно, то в конце дроби приписываются дополнительно нули. Примером служит следующее вычисление значения выражения 56,87:0,0001. В данном примере, так как после запятой насчитывается в делителе 4 знака, а в числе 56,87 – только 2 знака, то после них дописывается еще 2 нуля 56,8700, которые не меняют дробь. После переноса запятой получилось значение 568700.
Видеоурок заканчивается выводом на экран вопросов, на которые предлагается ответить ученикам. С помощью данных вопросов учитель может проверить, насколько хорошо усвоен учебный материал. Ученикам необходимо будет сформулировать правило деления десятичной дроби, которое выполняется на десятичную дробь, а также дроби 0,1, 0,01 и др. проверить. Как ученики понимают суть операции деления на дробь 0,01, можно выяснив, знают ли они о том, что деление на число 0,01 можно заменить умножением на 100.

Видеоурок «Деление на десятичную дробь» рекомендуется использовать на традиционном уроке математики в школе для повышения его эффективности. Учителю, выполняющему дистанционное обучение, видеоматериал будет полезен как наглядное пособие, помогающее более понятно представить ученику новый учебный материал. Видео может быть предложено для самостоятельной работы ученику, который недостаточно хорошо усвоил тему или самостоятельно изучает данную тему.
| Автор | |
|---|---|
| Дата добавления | 29.07.2014 |
| Раздел | Математика |
| Подраздел | Видеоурок |
| Просмотров | 7270 |
| Номер материала | 396 |