
Урок "Умножение десятичных дробей на натуральные числа"

Краткое описание документа:
Видеоурок «Умножение десятичных дробей на натуральные числа» - наглядный материал, который предназначен для повышения эффективности урока математики по данной теме. В ходе демонстрации представляется правило умножения десятичной дроби на натуральное число, подкрепляется наглядными примерами, как производятся данные действия на практике. Также представляется правило умножения десятичной дроби на круглые числа, подкрепляя правило примерами. Видео может использоваться в качестве наглядного материала, сопровождая объяснение учителя, или в качестве самостоятельной части урока. Освобожденное время при демонстрации видео учитель может использовать для углубления индивидуальной работы или проверки домашнего задания.
Наглядность материала обеспечивается с помощью приемов, улучшающих понимание и запоминание материала – анимационных эффектов, иллюстраций, цветного шрифта. Озвучивание видео дает возможность вставлять важные комментарии, облегчающие понимание темы, полностью заменяя учителя на этапе объяснения нового материала.
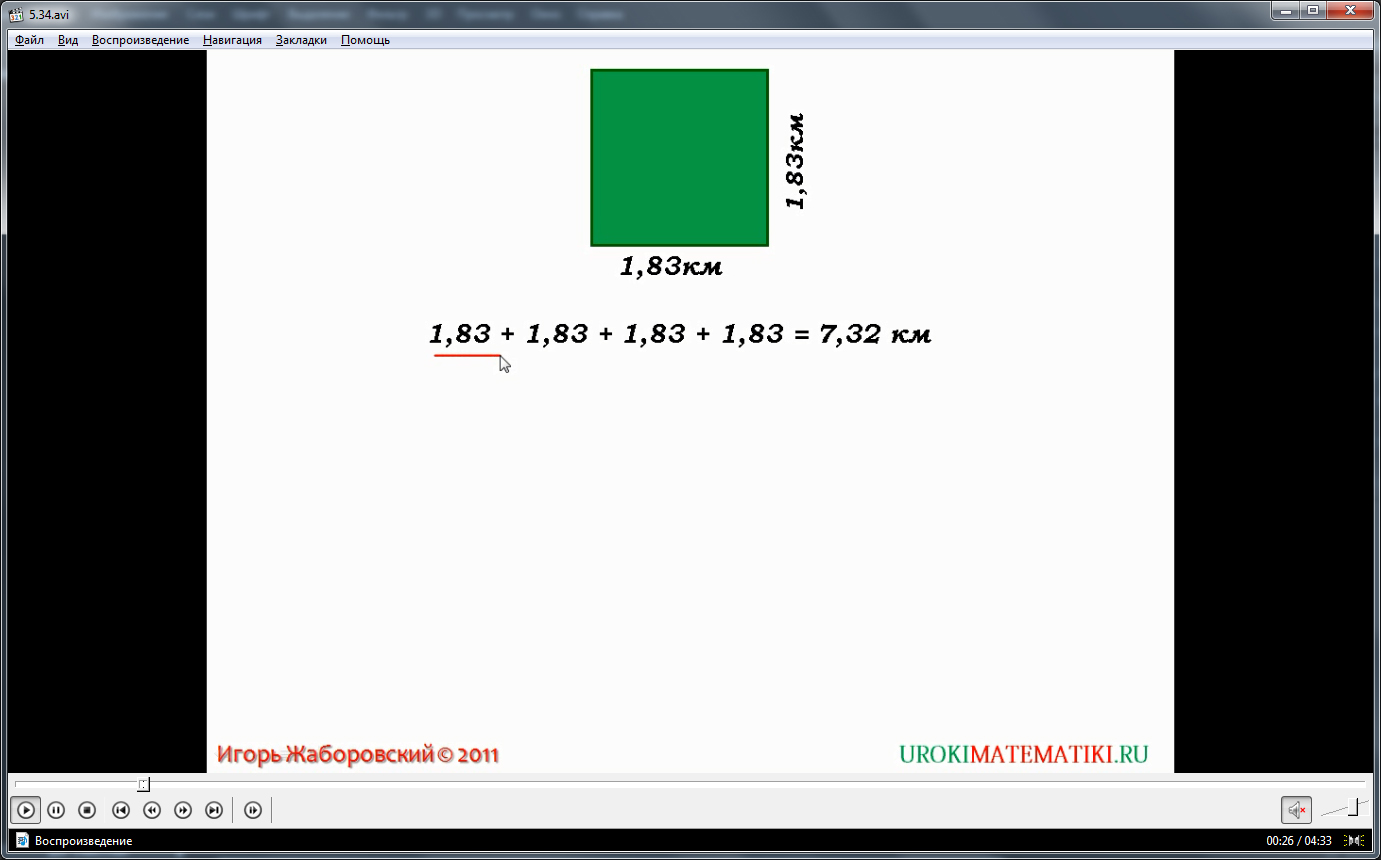
Демонстрация начинается с представления названия темы. Затем представляется прикладной пример, подводящий к задаче перемножения десятичного и натурального числа. Нужно решить задачу, в которой требуется найти периметр поля в форме квадрата. На экране изображается квадрат, сторона которого отмечена 1,83 км. Необходимо определить его периметр. Для этого длины всех четырех сторон квадрата складываются. На экране отображаются действия по нахождению периметра 1,83+1,83+1,83+1,83=7,32 км. Отмечается, что, так как сторон квадрате 4, то этот пример привел к необходимости перемножить десятичное число 1.83 с натуральным числом 4. Ниже формулируется определение понятия, что такое произведение десятичной дроби и натурального числа. Отмечается, что таким произведением называется сумма слагаемых, равных десятичному числу, а их количество равняется натуральному числу.
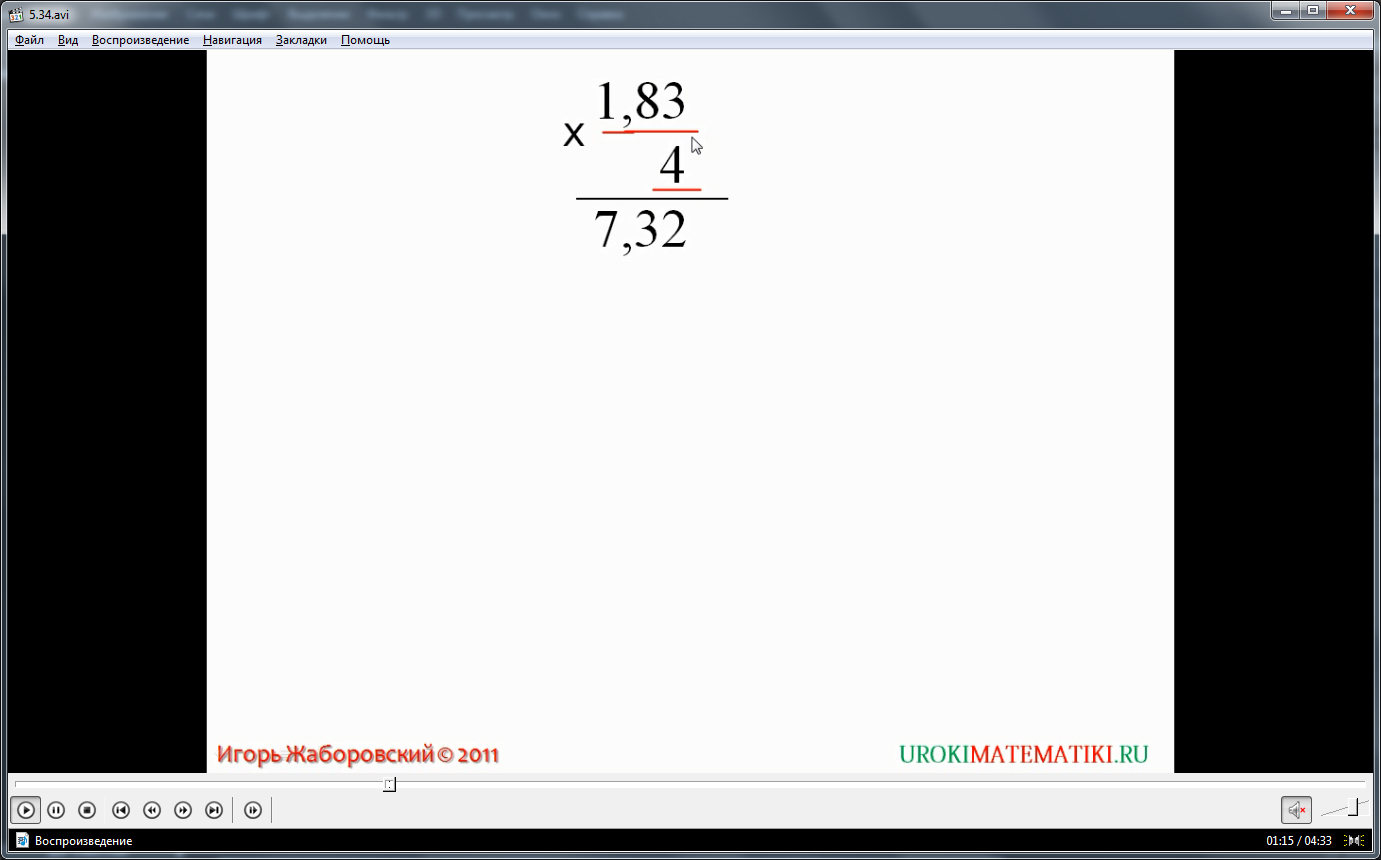
Описывается способ перемножения десятичного числа с натуральным числом в столбик. Обращается внимание учеников на важные моменты – натуральное число подписывается под десятичным числом так, чтобы последний разряд каждого числа были написаны друг под другом. Затем предлагается произвести вычисления, согласно правилу умножения натуральных чисел, опуская положение запятой. После вычисления необходимо поставить запятую, отсчитав от конца полученного числа столько разрядов, сколько отделено запятой разрядов в десятичном числе. В числе 1,83 отделено запятой 2 цифры, также отделяются цифры в произведении. Получается число 7,32.
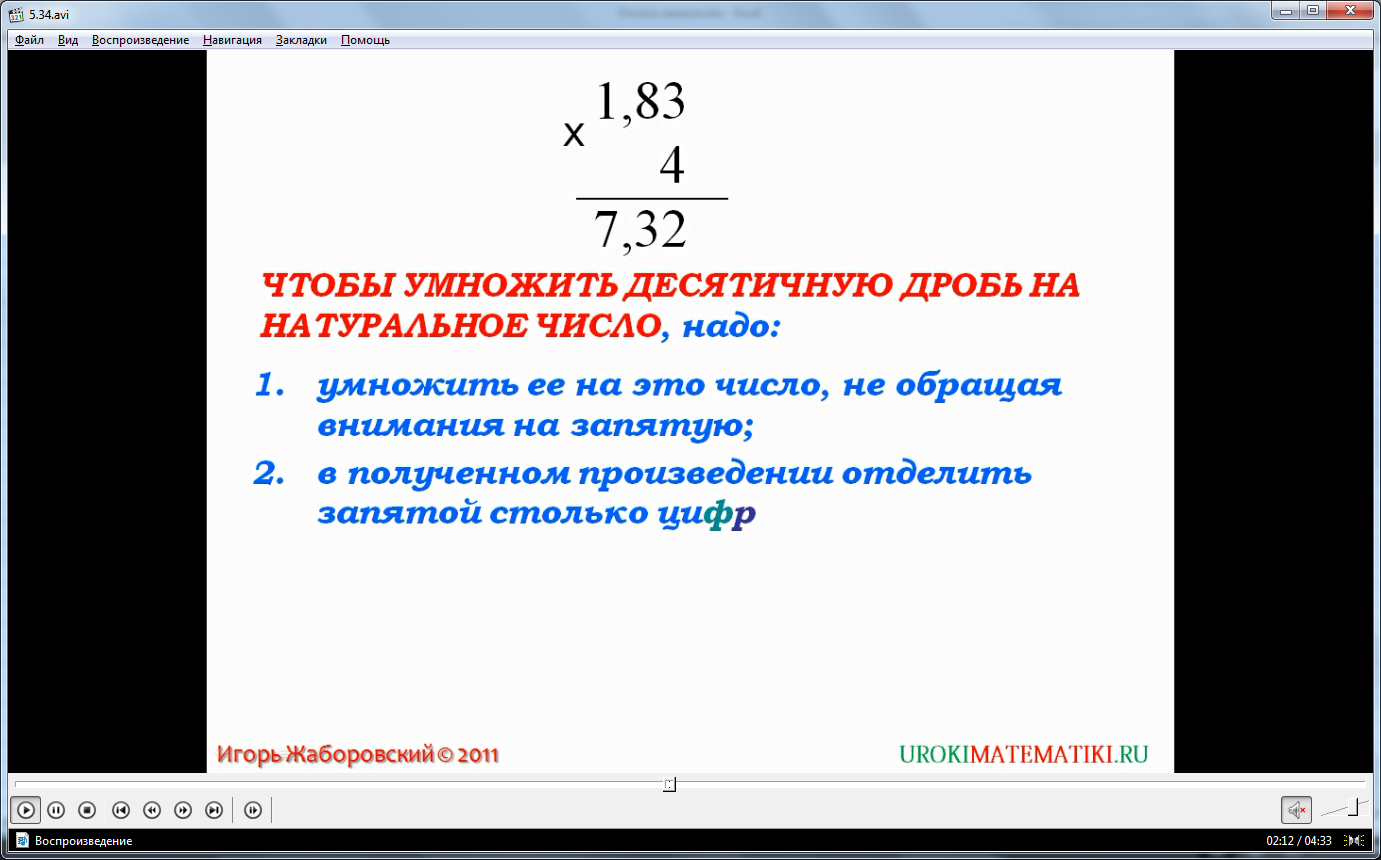
Ниже формулируется правило перемножения десятичной дроби и натурального числа. Правило состоит из двух пунктов, в которых отмечается, что сначала необходимо перемножить числа без учета того, что в первом есть запятая, а затем запятой нужно отделить столько разрядов слева, сколько разрядов отделено запятой в исходной десятичной дроби. Правило выделено цветным шрифтом, чтобы его было легче запомнить.
Рассматривается правило перемножения десятичной дроби с числами 10, 100, 1000 и др. Сначала приводятся примеры нахождения такого произведения. Дано число 9,865, которое необходимо умножить на 10. Согласно изученному правилу, сначала перемножаются числа без учета запятой 9865*10=98650. Затем отделяется запятой 3 знака справа – получается число 98,65. Отмечается, что такие действия можно упростить. Умножить дробь на 10 можно, просто перенеся запятую на один знак правее – было число 9,865, а после умножения его на 10, стало 98,65. Данный случай подтверждает общее правило, которое существует для нахождения произведения десятичной дроби с числами 10, 100, 1000 и др. Общее правило гласит, что в этом случае необходимо в десятичной дроби переставить запятую вправо на такое количество знаков вправо, сколько нулей имеется в натуральном числе, на которое умножается десятичная дробь.
Чтобы усвоить изученное правило, приводятся примеры произведения десятичной дроби с круглыми натуральными числами 10, 100 и др. В произведении 0,065·1000 запятая переносится на три знака вправо. Результатом вычисления является число 0065, где нули впереди можно не писать. В итоге получено число 65. Аналогично вычисляется результат перемножения 2,9·1000. Чтобы после запятой было три знака, приписываем к дробной части справа два нуля 2,900. После умножения данного числа на 1000, то есть перенесения запятой на три знака правее, получаем значение 2900.
Для закрепления пройденного материала ученикам предлагается ответить на вопросы. В числе ответов на вопросы им необходимо будет объяснить, что означает умножение десятичной дроби на натуральное число, сформулировать правило, как умножается десятичная дробь на натуральное число и объяснить правило умножения десятичной дроби на число 10, 100, 1000 и т.д.

Видеоурок «Умножение десятичных дробей на натуральные числа» рекомендуется применять на школьном занятии по данной теме для повышения эффективности обучения. Материал будет полезен для достижения целей урока учителю, проводящему дистанционное обучение. Также материал можно рекомендовать отстающим ученикам или желающим освоить данную тему самостоятельно.
| Автор | |
|---|---|
| Дата добавления | 28.07.2014 |
| Раздел | Математика |
| Подраздел | Видеоурок |
| Просмотров | 6002 |
| Номер материала | 394 |