
Урок "Аксиома параллельных прямых"

Краткое описание документа:
Видеоурок «Аксиома параллельных прямых» предполагает детальное рассмотрение важной аксиомы геометрии – аксиомы параллельных прямых, ее особенностей, следствий из данной аксиомы, широко применяющихся в практике решения геометрических задач. Задача данного видеоурока – облегчить запоминание аксиомы и ее следствий, сформировать представление о ее особенностях, применении при решении задач.
Подача материала в форме видеоурока открывает новые возможности для учителя. Подача ученикам стандартного блока учебного материала автоматизируется. При этом улучшается качество подачи материала, так как он обогащен наглядным представлением, анимационными эффектами, приближающими построения к реальным, проводимым на доске. Исторические сведения подаются с рисунками и фото, вызывая интерес к изучаемой теме. Видео также освобождает учителя для углубления индивидуальной работы во время обучения.
Сначала на данном видео демонстрируется название темы. Рассмотрение аксиомы начинается с построения ее модели. На экране изображены прямая а, лежащая вне ее точка М. Далее описывается доказательство утверждения, что через заданную точку М можно построить прямую, параллельную данной. Проводится перпендикулярно прямой а прямая с, затем перпендикулярно прямой с в точке М проводится прямая b. Основываясь на утверждении, о параллельности двух прямых, перпендикулярных третьей, отмечаем, что прямая b параллельна исходной прямой а. Учитывая это, указываем, что в точке М проведена прямая, параллельная данной. Однако необходимо еще проверить, есть ли возможность провести через М иную параллельную прямую. На экране показано, что любой поворот прямой b в точке М приведет к построению прямой, которая пересечет прямую а. Однако возможно ли доказать невозможность проведения другой прямой?
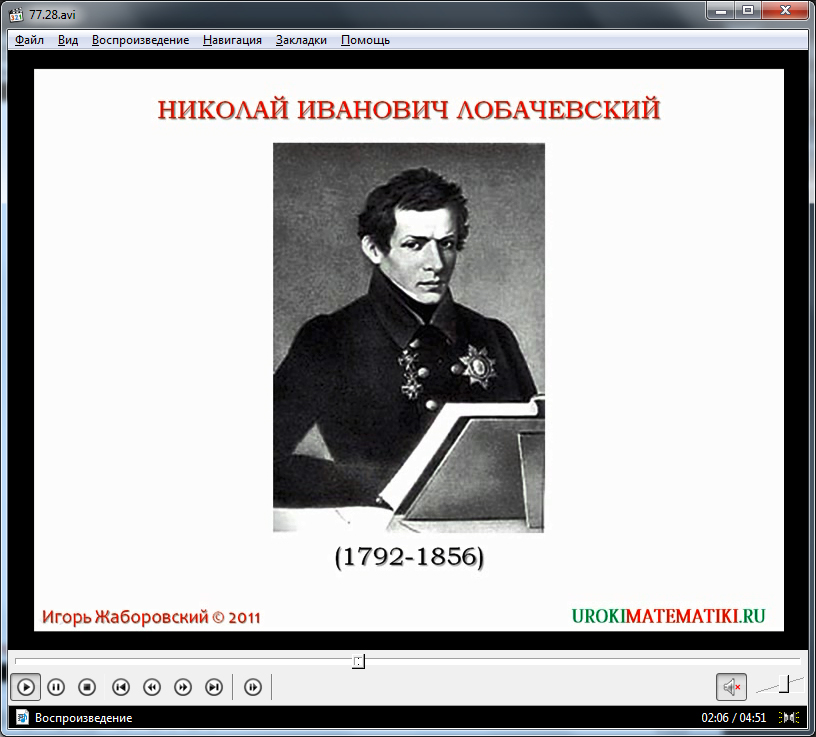
Вопрос доказательства невозможности проведения иной прямой, параллельной данной, имеет давнюю историю. Ученикам предлагается небольшой экскурс в историю вопроса. Отмечается, что в труде Евклида «Начала» данное утверждение приведено в виде пятого постулата. Попытки ученых доказать утверждение не привели к успеху. На протяжении многих веков математиков интересовала эта задача. Однако только в прошлом веке окончательно было доказано, что данное утверждение недоказуемо в евклидовой геометрии. Оно является аксиомой. Ученикам представляется один из знаменитых математиков, вложивших значительный вклад в математическую науку – Николай Иванович Лобачевский. Именно он сыграл важную роль в окончательном решении вопроса. Поэтому утверждение, рассматриваемое на данном уроке, является аксиомой, лежащей в фундаменте науки наряду с другими аксиомами.
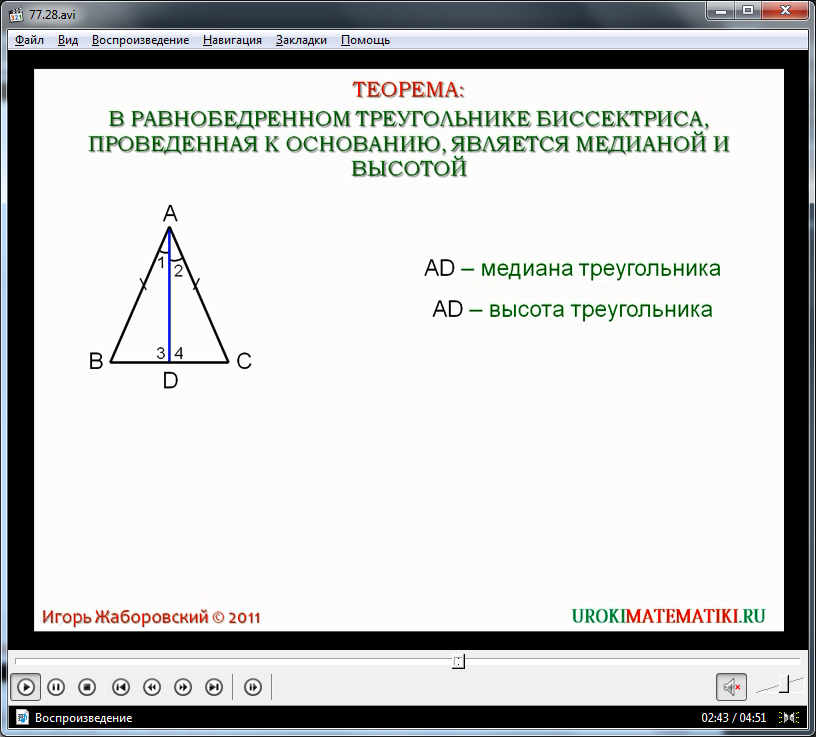
Далее предлагается рассмотреть следствия из данной аксиомы. Для этого необходимо уточнить понятие «следствия». На экране отображается определение следствий как утверждений, выводящихся непосредственно из теорем или аксиом. Данное определение может быть предложено ученикам для записи в тетрадь. Понятие следствий демонстрируется на примере, который уже рассматривался в видеоуроке 18 «Свойства равнобедренного треугольника». На экране выведена теорема о свойствах равнобедренного треугольника. Напоминается, что после доказательства данной теоремы рассматривались не менее важные следствия из нее. Так, если основная теорема утверждала, что биссектриса равнобедренного треугольника является медианой и высотой, то следствия имели близкое содержание, утверждая, что и высота равнобедренного треугольника является биссектрисой и медианой, а также медиана равнобедренного треугольника является одновременно биссектрисой и высотой.
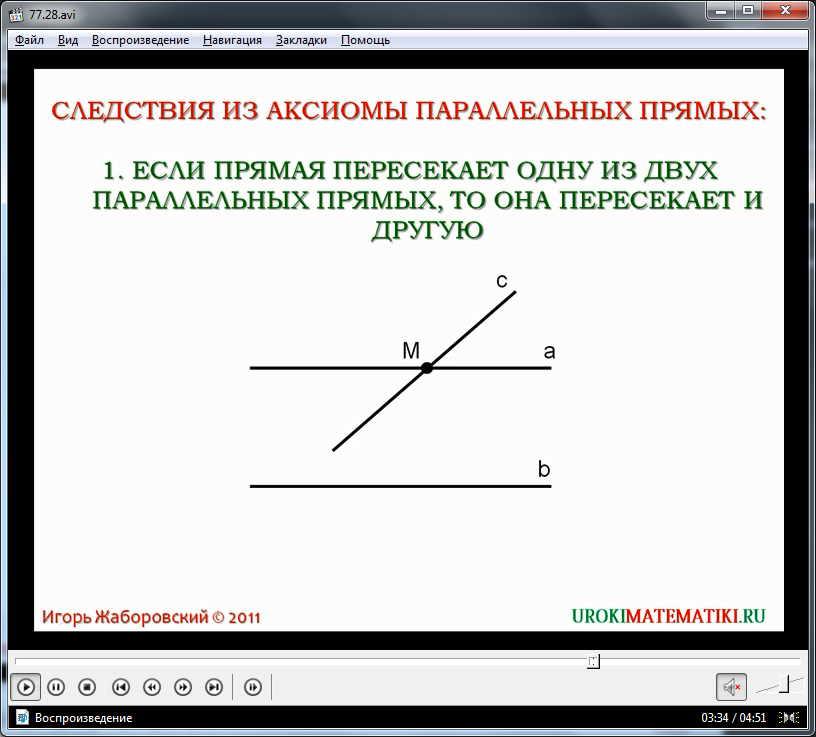
Уточнив понятие следствий, рассматриваются непосредственно следствия, выходящие из данной аксиомы параллельности прямых. На экране отображается текст первого следствия аксиомы, утверждающий, что пересечение прямой одной из параллельных прямых означает пересечение ею и второй параллельной прямой. На рисунке под текстом следствия изображается прямая b и параллельная ей прямая а. Вторая прямая пересекает прямую с в точке М, принадлежащей прямой а. Приводится доказательство утверждения, что прямая с пересечет также прямую b. Доказательство производится от противного, используя аксиому о параллельных прямых. Если предположить, что прямая с не пересекает b, это означает, что через данную точку можно провести еще одну прямую, параллельную указанной. Но это невозможно, учитывая аксиому параллельных прямых. Следовательно, с пересекает также прямую b. Следствие доказано.
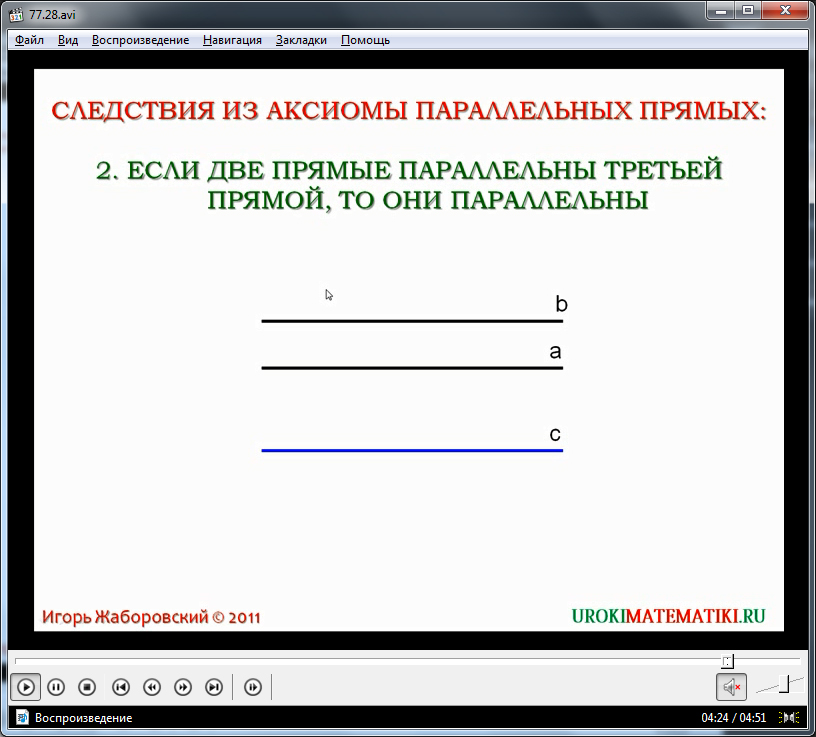
Далее рассматривается второе следствие из данной аксиомы. На экране отображается текст следствия, утверждающего, что если две прямые являются параллельными третьей, то можно утверждать о параллельности их между собой. На рисунке, демонстрирующем данное утверждение, построены прямые а, b, с. При этом прямая с как параллельная обеим прямым, выделена синим цветом. Предлагается доказать данное утверждение. В ходе доказательства допускается, что параллельные прямой с прямые а, b не являются параллельными между собой. Это означает, что они имеют точку пересечения. Это означает, что проходящие через точку М, обе прямые параллельны данной, что вступает в противоречие с аксиомой параллельных прямых. Данное следствие верно.
Видеоурок «Аксиома параллельных прямых» может облегчить учителю задачу объяснить ученикам особенности аксиомы, доказательства ее следствий, облегчить запоминание материала школьниками на обычном уроке. Также данный видеоматериал может быть использован при дистанционном обучении, быть рекомендованным для самостоятельного изучения.
| Автор | |
|---|---|
| Дата добавления | 02.08.2014 |
| Раздел | Геометрия |
| Подраздел | Видеоурок |
| Просмотров | 6321 |
| Номер материала | 515 |