
Презентация "Правило параллелепипеда"

Краткое описание документа:
Презентация «Правило параллелепипеда» представляет наглядный материал для освоения данной темы на уроке геометрии. Материал урока связывает знания, полученные учениками, о стереометрических телах, а также сведения из векторной алгебры. В ходе презентации ученики получают представление о правиле параллелепипеда, аналогичному правилу параллелограмма на плоскости, затем с помощью описания задач, в которых применяются изученные правила, формируется умение использовать полученные знания на практике.

Презентация решает несколько проблем, которые возникают в ходе изучения темы. С помощью использования наглядного пособия, разнообразия методов ведения урока, применения анимационных эффектов учитель удерживает внимание учеников на изучаемой теме. Также анимационные эффекты и возможность оформления слайдов в различных цветах улучшают представление объемных тел и построений, которые выполняются для рассмотрения их свойств. Благодаря выделению цветом, в построениях отмечаются детали, важные для понимания правила параллелепипеда, способа решения задачи.
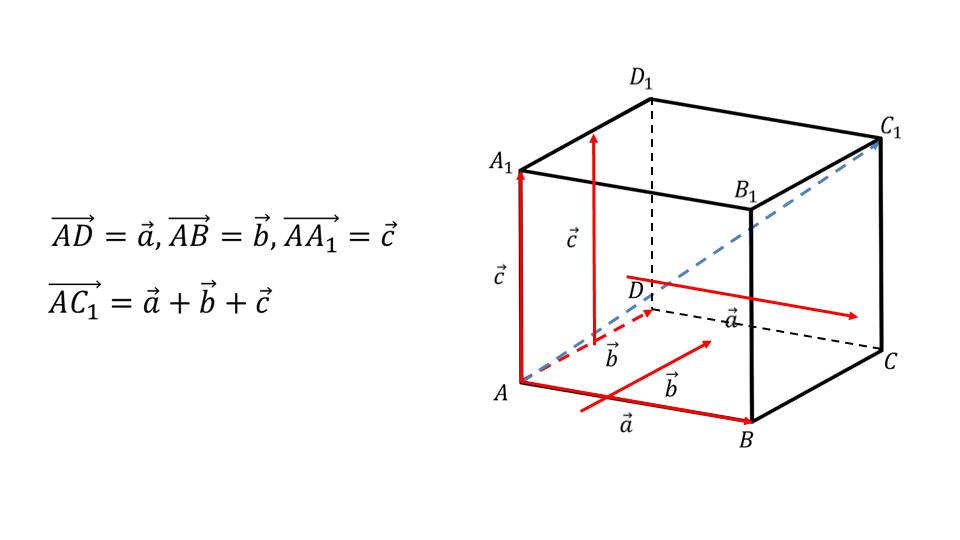
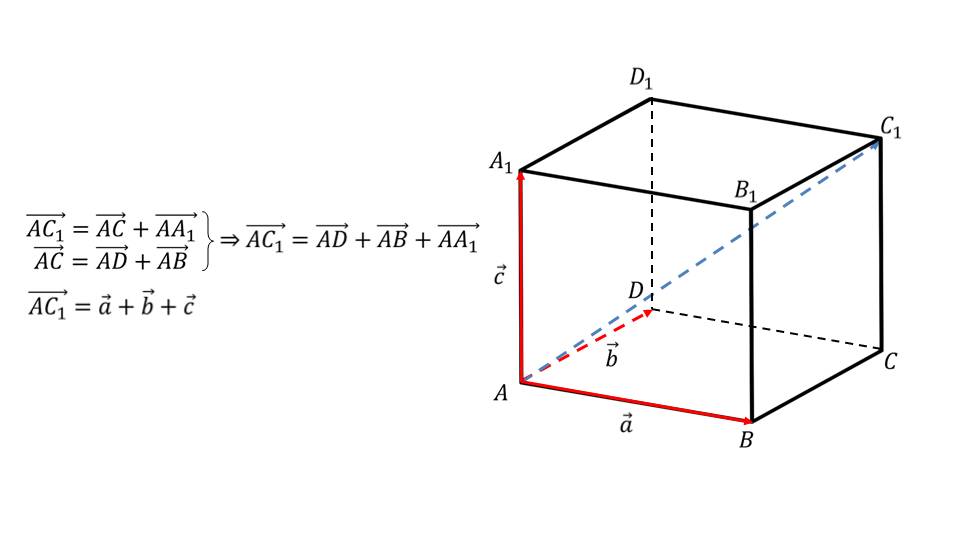
Демонстрация начинается с представления правила параллелепипеда, которое действует для векторов, лежащих в пространстве. Отмечается, что если из вершины параллелепипеда провести по трем его измерениям вектора, то суммарный их вектор будет располагаться на диагонали параллелепипеда. Определение выделено в рамку и рекомендуется для запоминания. Правило также демонстрируется на рисунке, на котором изображен параллелепипед ABCDA1B1C1D1, красным цветом выделены его измерения АВ, AD и AA1, на основе которых строятся векторы aˉ, bˉ, cˉ. Рядом с рисунком обозначены векторы, а также формула, отображающая рассматриваемое правило параллелепипеда AC1ˉ=aˉ+bˉ+cˉ. Описывается доказательство формулы. Используя правило параллелограмма, указываем сумму векторов AC1ˉ= ACˉ+ AА1ˉ, верную для диагональной плоскости AА1СC1, а также сумму векторов АСˉ=ADˉ+ABˉ для плоскости ABCD. Отсюда следует равенство AC1ˉ=ADˉ+ABˉ+AА1ˉ. Иначе данную формулу можно записать AC1ˉ=aˉ+bˉ+cˉ. Теорема доказана.
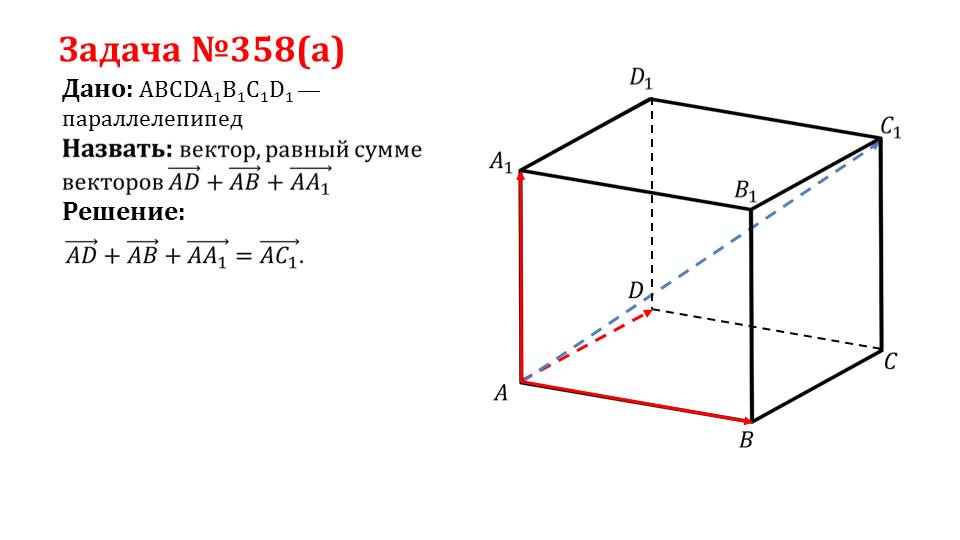
На слайде 4 описывается решение задачи 358(а). В задаче дан параллелепипед ABCDA1B1C1D1, в котором необходимо назвать вектор, что равен сумме векторов ADˉ+ABˉ+AА1ˉ. Решение сопровождается рисунком, на котором изображен параллелепипед ABCDA1B1C1D1, в котором красным цветом выделены измерения, на которых строятся векторы. Пользуясь правилом параллелепипеда, находим решение задачи ADˉ+ABˉ+AА1ˉ= AC1ˉ. Найденный вектор AC1ˉ отмечен на рисунке синим цветом.
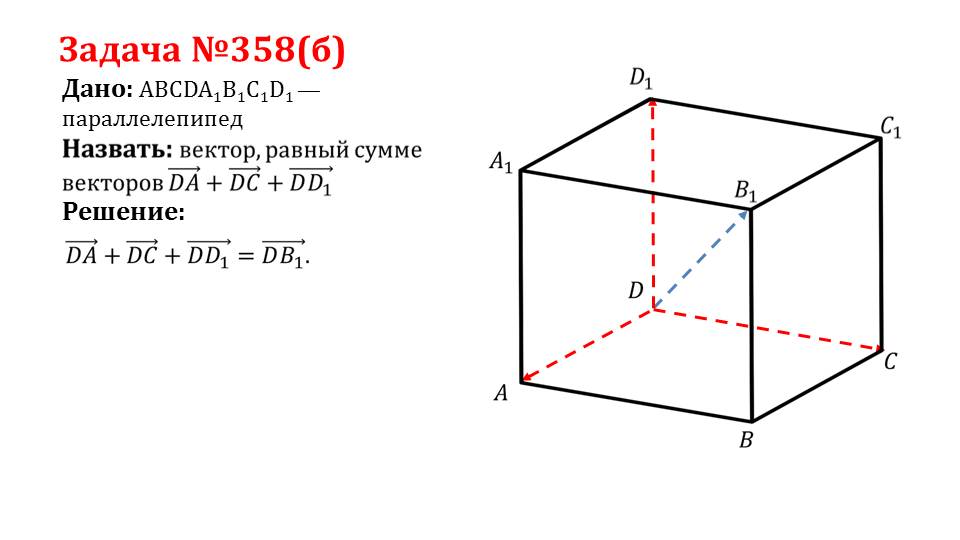
На слайде 5 необходимо найти суммарный вектор векторов DAˉ, DCˉ, DD1ˉ. В решении задачи 358(б) также применяем правило параллелепипеда. Найденный суммарный вектор DAˉ+DCˉ+DD1ˉ= DВ1ˉ.
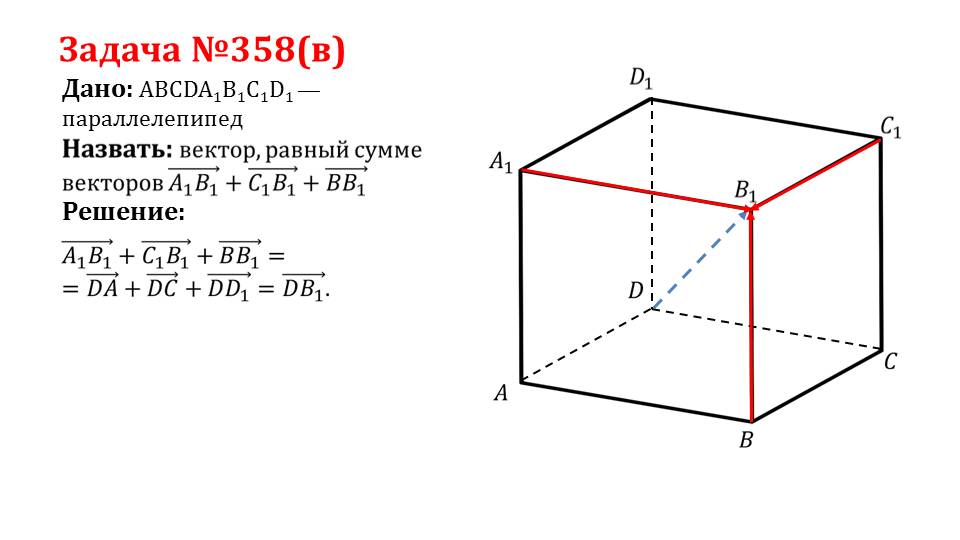
Следующий слайд демонстрирует решение задачи 358(в), в которой необходимо найти суммарный вектор векторов A1B1ˉ, С1B1ˉ, ВB1ˉ, которые представляют измерения прямоугольного параллелепипеда, сходящиеся в одной вершине. Пользуясь равенством сторон параллелепипеда, можно утверждать, что A1B1ˉ+ С1B1ˉ+ ВB1ˉ=DAˉ+DCˉ+DD1ˉ Очевидно, что при сложении данных векторов образуется вектор диагонали параллелепипеда DВ1ˉ.
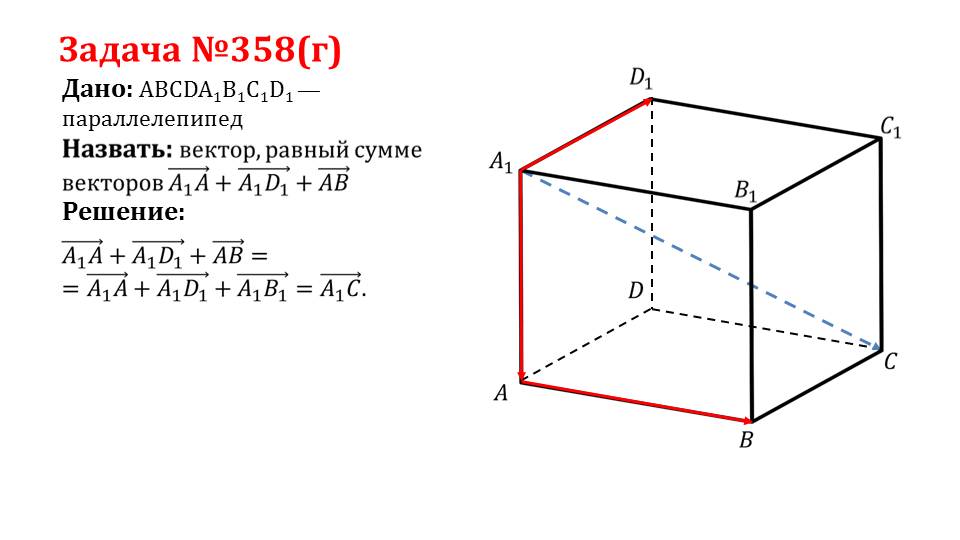
В задаче 358(г), решение которой описано на слайде 7, дан параллелепипед ABCDA1B1C1D1, в котором нужно найти сумму векторов A1Аˉ, A1D1ˉ, ABˉ. Пользуясь равенством сторон параллелепипеда, можно представить сумму векторов A1Аˉ+ A1D1ˉ+ A1B1ˉ= A1Сˉ. Решение сопровождается рисунком, на котором отмечены соответствующие стороны параллелепипеда, а также диагональ A1Сˉ - суммарный вектор.
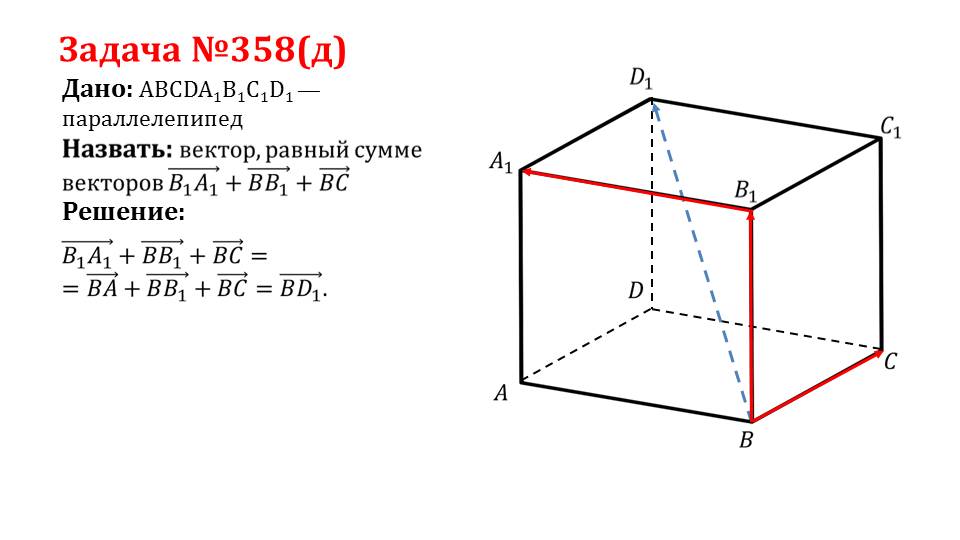
Последний слайд представляет решение задачи 358(д). В задаче дан параллелепипед ABCDA1B1C1D1, в котором необходимоопределить сумму векторов B1A1ˉ, ВB1ˉ, BCˉ. Пользуясь параллельным переносом вектора B1A1ˉ в вершину В, получаем равнозначное выражение для суммы векторов BAˉ+ВB1ˉ+BCˉ. В данном параллелепипеде суммарный вектор является диагональю BD1ˉ. Решение задачи сопровождается рисунком, где выполнено построение параллелепипеда ABCDA1B1C1D1,, красным цветом выделены вектора, над которыми выполняется операция, а также пунктирной линией отмечена суммарная диагональ.
Презентация «Правило параллелепипеда» рекомендуется для использования на традиционном уроке в школе для повышения его эффективности. Материал может подкреплять наглядностью объяснение учителя в ходе дистанционного обучения. Ученики, которым недостаточно урока для глубокого понимания темы, могут использовать презентацию для самостоятельной работы.
| Автор | |
|---|---|
| Дата добавления | 28.10.2014 |
| Раздел | Геометрия |
| Подраздел | Презентация |
| Просмотров | 4017 |
| Номер материала | 913 |