
Презентация "Признаки равенства прямоугольных треугольников"

Краткое описание документа:
Мы говорили, что свойство прямоугольных треугольников вытекает из свойств треугольников общего вида и наличия в них прямого угла. Это же и относится к признакам равенства прямоугольных треугольников. То есть, повторяя признаки равенства произвольных треугольников, мы изучаем признаки равенства прямоугольных треугольников.


слайды 1-2 (Тема презентации "Признаки равенства прямоугольных треугольников", признаки)
Обратим внимание на первый признак идентичности, где говорится о равенстве треугольников при равенстве их катетов. Давайте обратим внимание на формулировку на доске. Представим, что у нас есть треугольник «САВ», а также визуально идентичный ему треугольник «С1А1В1». Известно, что оба являются прямоугольными, т.е. угол «С» равен девяносто градусов и угол «С1» девяносто градусов. Далее, знаем, что «АС» и «А1С1» идентичны, а вторые катеты «ВС» и «В1С1» тоже схожи по параметрам. Обратимся к признакам произвольного треугольника для доказательства этого признака.
Если произвольному треугольнику характерно равенство углов (например, углы «С» и «С1» идентичны), а прилежащие стороны схожи между собой по параметрам, то по первому признаку мы знаем о равенстве таких произвольных треугольников. Вернёмся к прямоугольному треугольнику. Нам известно, что угол «С» и угол «С1» - прямые, то есть равны по девяносто градусов, а прилежащие катеты показывают равенство между собой. Следовательно, вытекает, что эти два прямоугольных треугольника схожи по проанализированным параметрам.
Нам также известно, что есть характерные идентичности у произвольных треугольников. Второй признак точно так же вытекает из идентичного ему признака у прямоугольных, где их равенство доказывается равенством любого катета и рядом находящегося острого угла. Это утверждение верно, так как в наших фигурах есть ещё прямые углы, которые равны между собой.

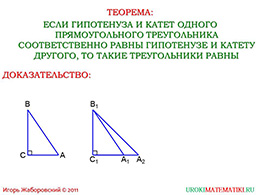
слайды 3-4 (теоремы)
Пока мы рассмотрели характерные параметры у первого и второго признаков идентичности. Перейдём к третьему признаку их схожести, где идентичность треугольников зависит от схожести наиболее длинной стороны (в нашем случае – гипотенузы) и острого угла двух фигур (в нашем случае - прямоугольных треугольников).
Итак, в исследуемом примере есть две фигуры «АВС» и «А1В1С1». Нам известно следующее: угол «В» и «В1» имеют девяносто градусов каждый; гипотенуза «АВ» идентична гипотенузе второго треугольника «А1В1»; острый угол «А» равен «А1». Попробуем доказать равенство треугольников. Если у нас углы острые равны, то вторые острые углы тоже будут равны (при помощи дополнения всей суммы до ста восьмидесяти градусов). Так как углы «А» и «А1» равны, следует, что углы «В» и «В1» тоже равны. Если хотя бы один острый угол проявляет равенство в двух фигурах, то и вторые острые углы в прямоугольных треугольниках показывают схожесть между собой. Следовательно, треугольники идентичны по стороне и прилежащим углам. Что и требовалось доказать.
Мы доказали идентичность параметров прямоугольного треугольника. Именно они являются следствием из признаков равенства прямоугольных треугольников. Остался один специфический признак равенства прямоугольного треугольника, где равенства таких треугольников зависит от равенства гипотенузы и одного катета. Имеем треугольники «АВС» и «А1В1С1», про которые известно наличие прямых углов «С» и «С1», равенство гипотенуз «АВ» и «А1В1», а также катетов «ВС» и «В1С1». Специфика в том, что у нас есть две равные стороны, но мы не знаем, равны ли углы между ними. То есть имеется признак по двум сторонам и большему углу, который не лежит между ними. Совмещаем треугольники наложением. Мы знаем точное расположение точки «В» и «В1», потому что известно равенство катетов «ВС» и «В1С1». Однако нам неизвестно совместимы ли точки «А» и «А1», поэтому пойдём от противного: точки «А» и «А1» несовместимы. Тогда смотрим на новый треугольник «А1В1А2» и понимаем, что он должен быть равнобедренным, а значит и углы у основания тоже. Но мы видим абсолютно несоответствие данного противоречия, поэтому точки «А» и «А1» совпадают и прямоугольные треугольники равны.
| Автор | |
|---|---|
| Дата добавления | 02.08.2014 |
| Раздел | Геометрия |
| Подраздел | Презентация |
| Просмотров | 5053 |
| Номер материала | 263 |