
Урок "Некоторые свойства прямоугольных треугольников"

Краткое описание документа:
Видеоурок «Некоторые свойства прямоугольных треугольников» представляет учебный материал по данной теме. Задача данного урока – облегчить усвоение материала по теме, представить наглядно и понятно для учеников утверждение и доказательство теорем, отражающих некоторые свойства прямоугольных треугольников.
Основное преимущество рассматриваемого видеоурока – наглядность, которая помогает учителю объяснить тему рока, концентрирует внимание учеников на изучаемом предмете, облегчает запоминание утверждений и доказательств.
В начале видеоурока, после представления его темы, ученикам предлагается вспомнить теорему о сумме углов треугольника, которая является основой для выявления многих других свойств треугольников различных видов. В данной теме рассматриваются особенности прямоугольных треугольников, доказательство которых опирается на данную теорему.
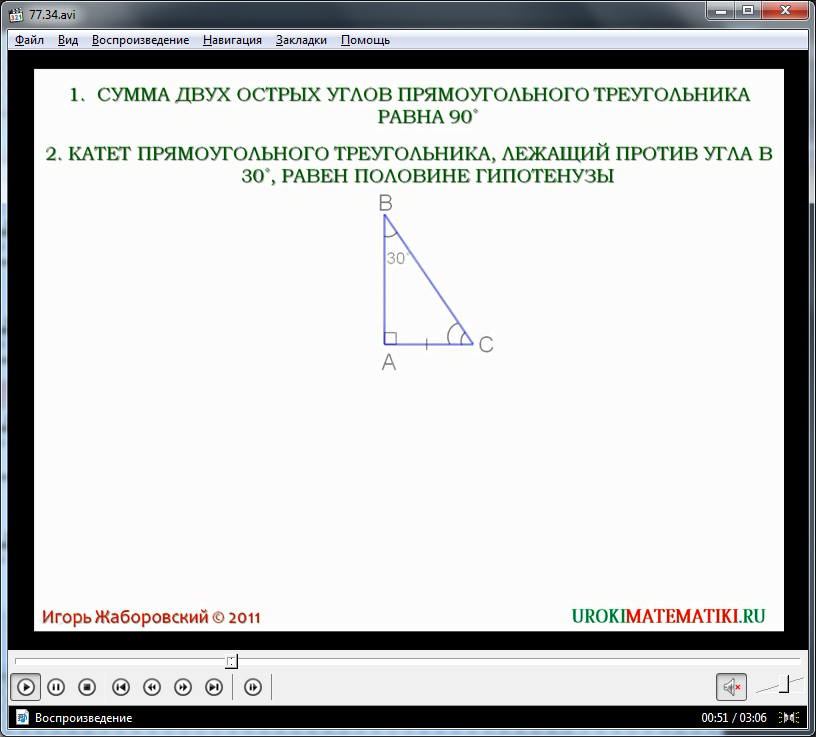
Формулируется и выводится на экран первое свойство прямоугольного треугольника о том, сумма двух его острых углов равна 90°. Это утверждение следует из того, что сумма углов любого треугольника 180°, а в прямоугольном треугольнике один угол прямой, следовательно, сумма двух оставшихся острых углов будет 90°.
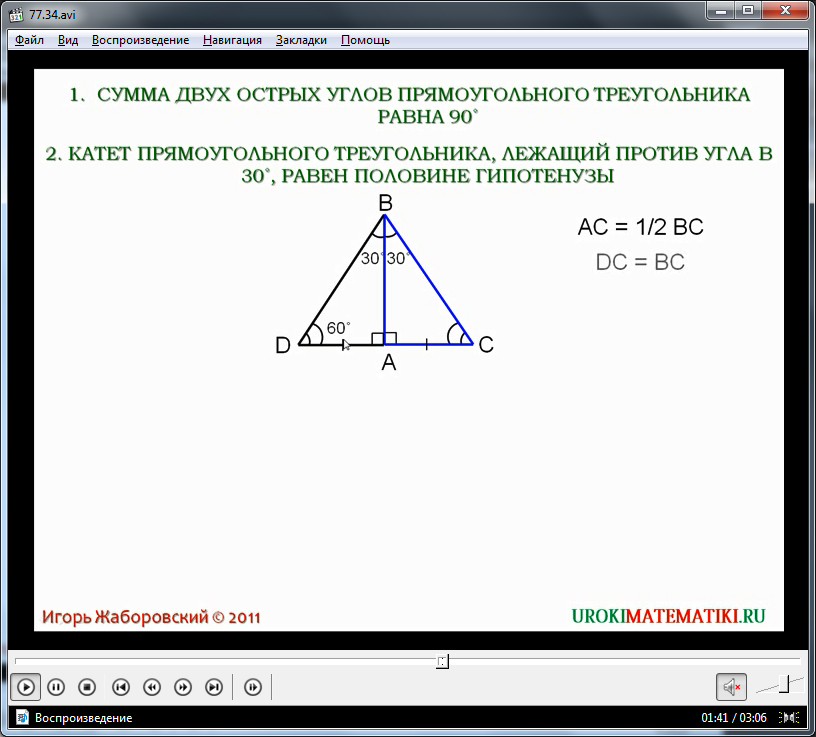
Второе рассматриваемое свойство – величина катета, лежащего напротив угла 30° в прямоугольном треугольнике равна половине гипотенузы. Для доказательства данного свойства рассматривается треугольник ΔABC, построенный на экране рядом с текстом рассматриваемого свойства. В треугольнике отмечены прямой угол ∠A, угол ∠B=30°. Необходимо доказать, что AC=(1/2) BC. Для этого к треугольнику ΔABC достраивается равный ему треугольник ΔABD таким образом, чтобы сторона AD лежала со стороной AC на одной прямой. При этом угол ∠DBA=∠ABC=30°. Общая величина угла ∠DBC равна 60°. Это равно также величине угла ∠BDC и ∠BCD. Так как напротив равных углов и стороны треугольника также будут равны, то сторона AC равна половине стороны BC. Это и нужно было доказать.
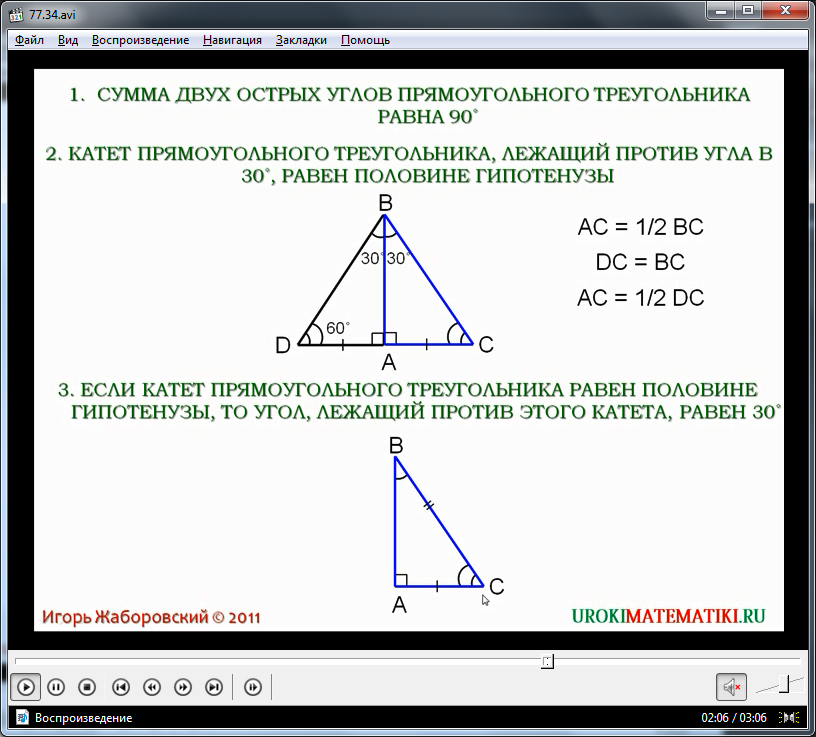
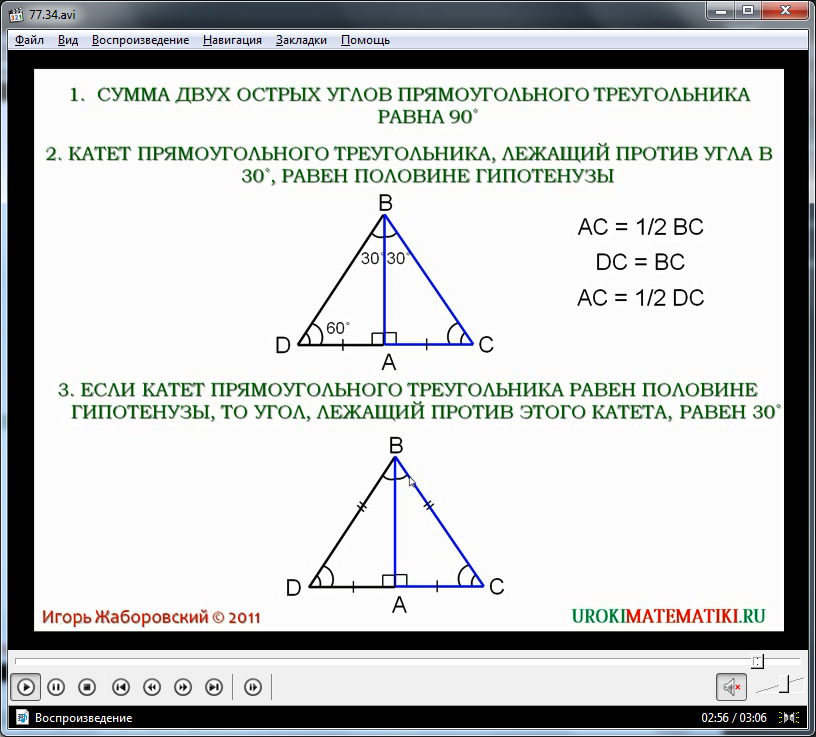
Третье свойство, рассматриваемое в данной теме, говорит о том, что равенство катета прямоугольного треугольника половине гипотенузы свидетельствует о том, что напротив нее лежит угол 30°. Для доказательства утверждения рассматривается изображенный ниже прямоугольный треугольник ΔABC. По условию данного утверждения, имеем AC=(1/2) BC. Необходимо доказать, что угол ∠ABC=30°. Для доказательства, аналогично предыдущему доказательству, к треугольнику ΔABC достраиваем равный ему треугольник ΔABD. В результате построения получается равносторонний треугольник ΔBCD, так как AC=(1/2) BC и в результате построения DC=2AC. Соответственно, все углы данного треугольника по 60°. Но известно, что величина угла ∠DBC – удвоенный угол ∠ABC. А это значит, что ∠ABC=30°. Утверждение доказано.
Видеоурок «Некоторые свойства прямоугольных треугольников» понятно и наглядно представляет материал урока, ход рассуждений при доказательстве теорем. Поэтому данный видеоурок может быть рекомендован не только учителю для наглядного объяснения темы урока, но и ученикам для самостоятельного изучения. Также видео поможет объяснить учебный материал при дистанционном обучении.
| Автор | |
|---|---|
| Дата добавления | 02.08.2014 |
| Раздел | Геометрия |
| Подраздел | Видеоурок |
| Просмотров | 7333 |
| Номер материала | 521 |