
Презентация "Теорема о вписанном угле"

Краткое описание документа:
Следующее понятие, которые связаны с изучением, непосредственно, окружности, это «вписанная окружность в некоторый многоугольник». Не которые фигуры могут быть расположены в окружности, или же, окружность может располагаться в некоторой фигуре.
В данной презентации будут рассматриваться вписанные углы. Речь идет о центральных углах. Они рассматривались в предыдущем уроке. Можно просмотреть предыдущую презентацию и восстановить информацию.

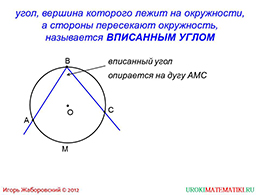
слайды 1-2 (Тема презентации "Теорема о вписанном угле", определение вписанного угла)
Итак, на первом слайде дается иллюстрация, на которой изображена окружность и вписанный в него угол ABC. Из рисунка видно, на какую дугу она опирается. Стороны такого угла, должны пересекать окружность. В таком случае, этот угол можно назвать вписанным в окружность. Если учитель объясняет урок по данной презентации, то он может предложить присутствующим восьмиклассникам начертить в тетради собственный пример вписанного угла в окружность.
На следующем слайде объясняется, каким образом необходимо найти меру вписанного угла? Для этого стоит вспомнить, что такое мера дуги, ведь в приведенной ниже формуле используется это понятие. Итак, вписанный угол равняется половине меры дуги, на которую она, собственно, опирается. При записи этой формулы, желательно, чтобы школьники обвели ее в квадрат, подчеркнули или выделили любым другим способом.
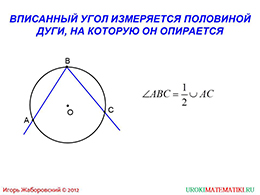
слайды 3-4 (измерение вписанного угла, пример)
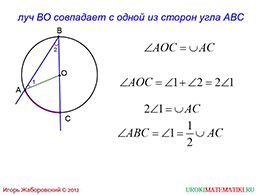
На следующих слайдах презентации «Теорема о вписанном угле» будут рассматриваться различные случаи, касательно некоторого луча BO, который начинается от вершины вписанного угла и проходит через центр окружности.
В первом случае, данный луч совпадает с одной из сторон внутреннего угла. Рассматривается верность теоремы о вписанном угле для этого случая. После проведения доказательства, получаем изначально записанную формулу.
На следующем слайде рассматривается другой пример. Луч BO делит вписанный угол ABC на два угла. Верна ли теорема в данном случае?
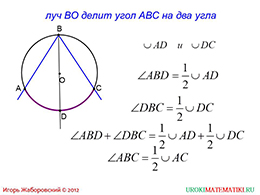
слайды 5-6 (примеры)
Если рассмотреть подробнее, то можно убедиться, что она действительно «работает» и в этом случае. Если хорошо объяснить доказательства, то школьник сможет воспроизвести его в дальнейшем самостоятельно. Не стоит жалеть время на объяснения доказательств.
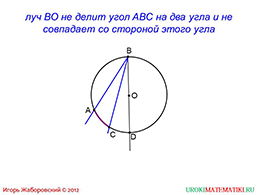
И, наконец, рассмотрим третий случай. Мы видим, что луч находится не внутри вписанного угла, то есть не делит его на два угла, не совпадает ни с одной стороной.
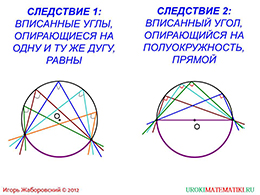
После рассмотрения теоремы на разных примерах, можно перейти к изучению их следствий, которые приведены на данном слайде. Первое следствие говорит о том, что зная, что вписанный угол равен половине меры дуги, на которую она опирается, можно прийти к выводам, что все подобным образом построенные вписанные, то есть опирающиеся на эту же дугу, углы будут равны. Следствие проиллюстрировано на чертеже.
слайды 7-8 (следствия из теоремы)
Чуть правее приводится второе следствие. Если вписанный угол опирается на полуокружность, то он является прямым. Таких углов можно начертить бесконечное множество.
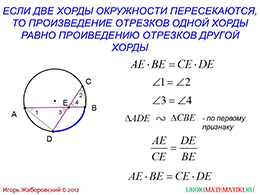
На завершающем слайде приводится утверждение, которое касается хордам окружности. Если провести любые две пересекающиеся хорды, то в результате получим четыре отрезка. Произведение отрезков одной из хорд, равен аналогичному произведению второй хорды.
| Автор | |
|---|---|
| Дата добавления | 01.08.2014 |
| Раздел | Геометрия |
| Подраздел | Презентация |
| Просмотров | 6863 |
| Номер материала | 351 |