
Урок "Градусная мера дуги окружности"

Краткое описание документа:
В нашей серии видео уроков мы познакомились с несколькими типичными фигурами в геометрии, а также сопутствующими им свойствами. Используя наглядные примеры, мы проиллюстрировали доказательства важнейших теорем, которые поспособствуют решению множества математических задач. В нынешнем видео мы ознакомимся с окружностью и её дугой.
Окружность – это геометрическая фигура, образуемая множеством равноудаленных точек, которые ориентированы от некоего общего центра, именуемого центром всей окружности. По сути, это правильная замкнутая кривая, охватывающая максимально возможную площадь. Не стоит путать окружность и круг – окружностью именуют только саму внешнюю кривую, набор точек. Помимо этого, окружность может иметь только центр-точку или отрезки, соединяющие точки на окружности (хорда или дуга). Круг же обладает внутренней площадью; на нем строятся плоские фигуры, такие как сегмент и сектор. Важнейшим элементом любой окружности является её радиус – отрезок, соединяющий любую точку на кривой и центр. Собственно, линейный размер радиуса и задает саму окружность.
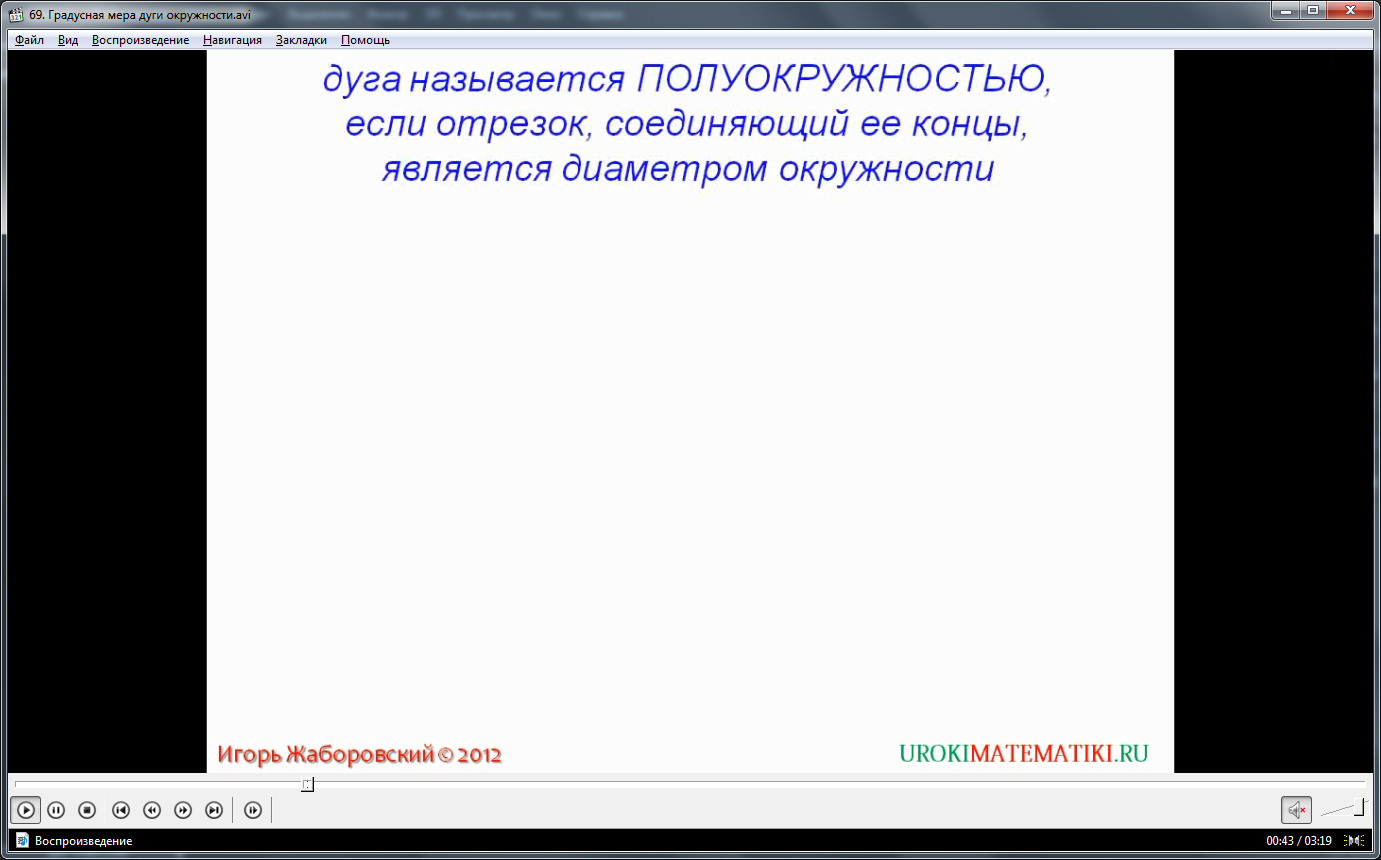
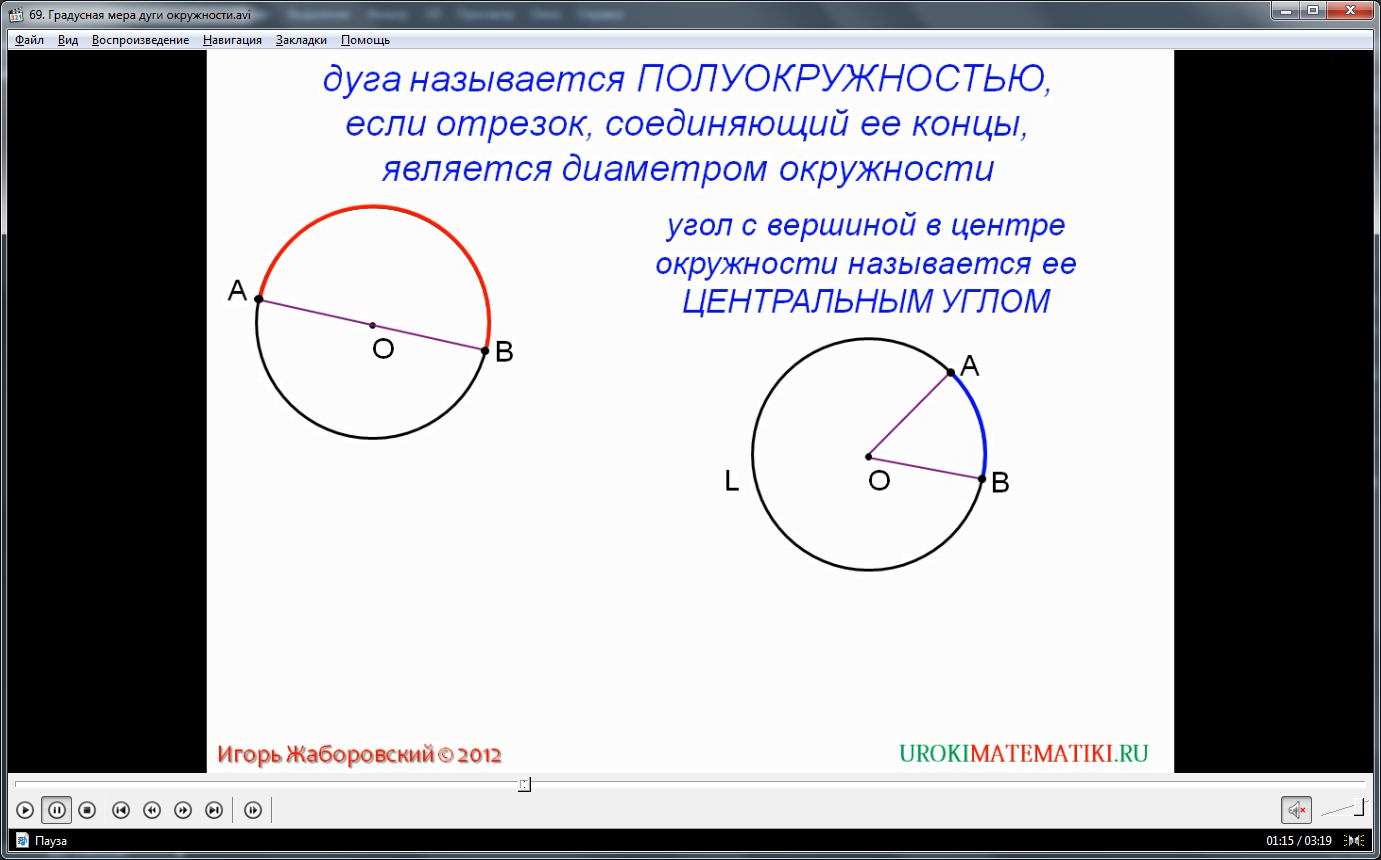
Участок кривой на окружности, лежащий между двумя произвольными точками, именуется дугой. Стоит отличать её от хорды, которая также соединяет произвольные точки, но напрямую, отдельным отрезком. На представленном видео удобно рассматривать частные случаи дуги, которые зависят от её углового размера. Дуга аннулируется, если точки сливаются в одну. В случае, когда концы дуги совпадают с точками единого диаметра (двойного радиуса) –дуга именуется полуокружностью. Если крайние точки дуги, охватывающей окружность, почти полностью, бесконечно сближаются, то дуга сама перерастает в полноценную окружность.
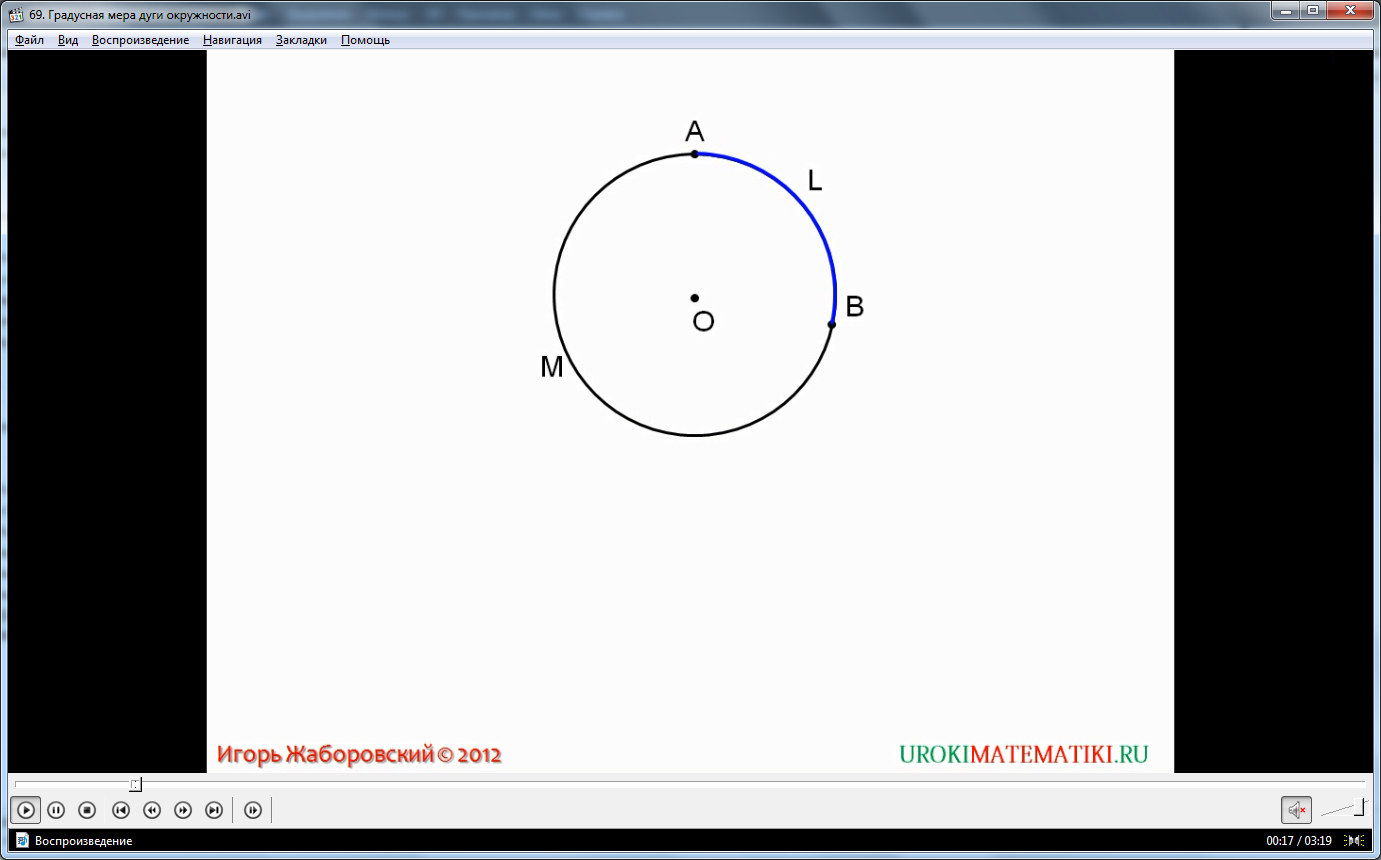
Важнейшей особенностью любой дуги является то, что она всегда существует в паре со своим антиподом. Для создания дуги нужны две любые разные точки на окружности, и они породят ровно две дуги. Например, на окружности с центром О возьмем две точки – А и В. Они образуют дуги АВ и ВА.
Угол, который лежит напротив дуги, часто именуют центральным. Вообще, любой угол с вершиной в центре окружности называется центральным для этой фигуры. Но подобный угол всегда будет отсекать сторонами (или продолжениями сторон) определенную дугу на окружности. Между величиной угла и линейными размерами дуги существует строгая зависимость – чем больший угол, тем большую дугу он отсекает. Собственно говоря, дугу можно физически задать двумя параметрами – длиной (в единицах длины, соответственно) кривой от А до В, либо же угловой величиной (в единицах плоского угла – в град или рад), соразмерной со значением центрального угла для данной дуги.
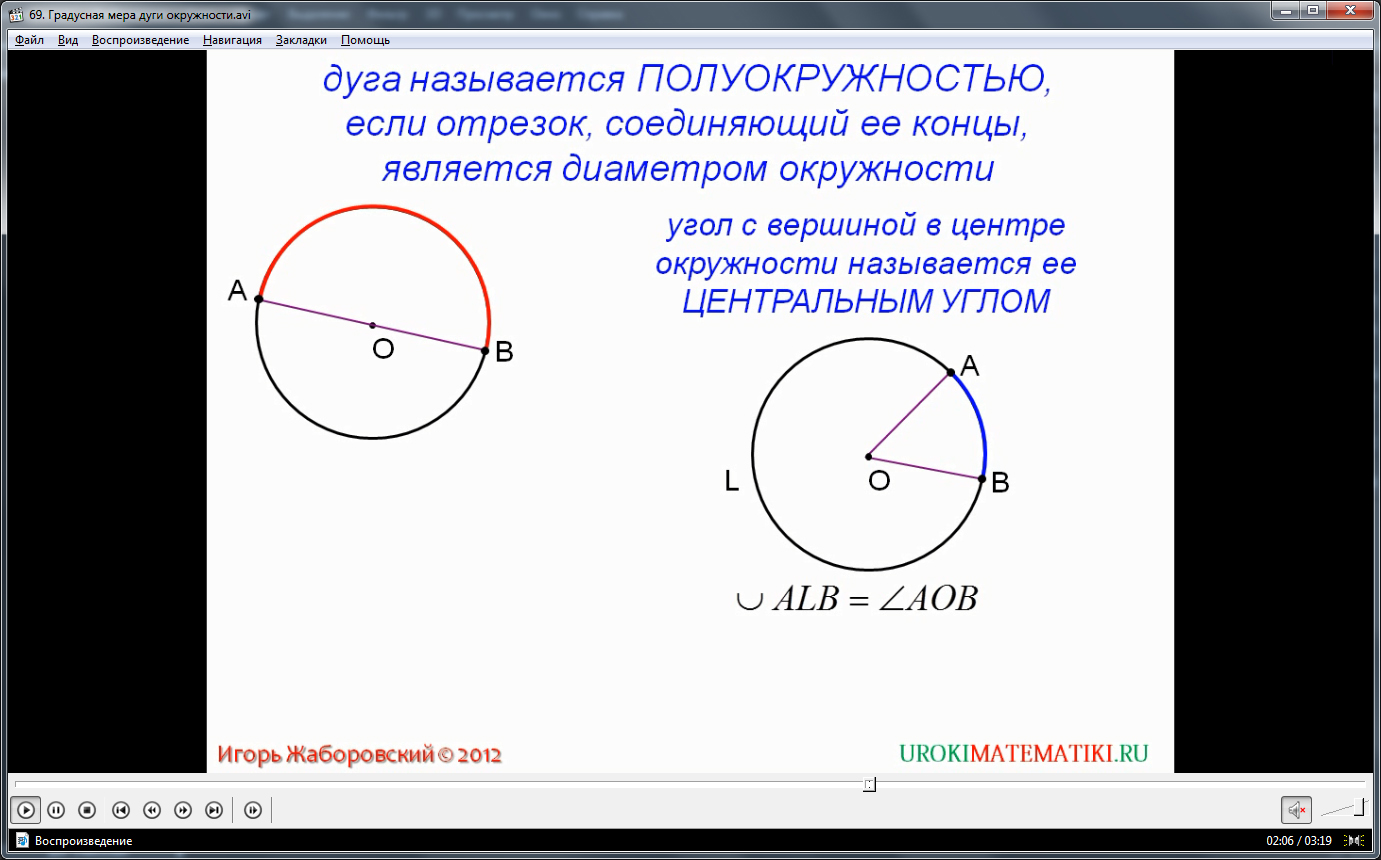
Более того, зависимость между углом при центре окружности и дугой, отсекаемой им, используется для определения внесистемной единицы плоского угла – радиана. Значение в один радиан имеет плоский угол, который отсекает на окружности дугу, равную радиусу этой окружности, при условии, что центр окружности и вершина угла совпадают в пространстве. Радиан равен значению в чуть менее 60 градусов. При этом линейные размеры радиуса и самой окружности во внимание не берутся. Чаще всего дугу измеряют именно в угловой мере, ориентируясь на числовое значение радиан. Иногда, для простоты, используются и градусы.
Важнейшее свойство дуг на окружности – сумма угловых значений двух дуг, образованных одной и той же парой точек на окружности, всегда равна 360 градусам или чуть более 6 радианам. В частном же случае, угловой размер полуокружности равен 180 градусам
| Автор | |
|---|---|
| Дата добавления | 01.08.2014 |
| Раздел | Геометрия |
| Подраздел | Видеоурок |
| Просмотров | 8779 |
| Номер материала | 607 |