
Урок "Значение синуса, косинуса и тангенса для углов 30, 45 и 60 градусов"

Краткое описание документа:
В предыдущих видео занятиях мы рассмотрели главные тригонометрические термины – синус, косинус и тангенс угла. Напомним, что синусом угла называется значение соотношения между противолежащим катетом и гипотенузой; косинусом угла называется соотношение между прилежащим катетом и гипотенузой; тангенсом угла называется соотношение между противолежащим и прилежащим катетом. При условии прямоугольности треугольника, разумеется.
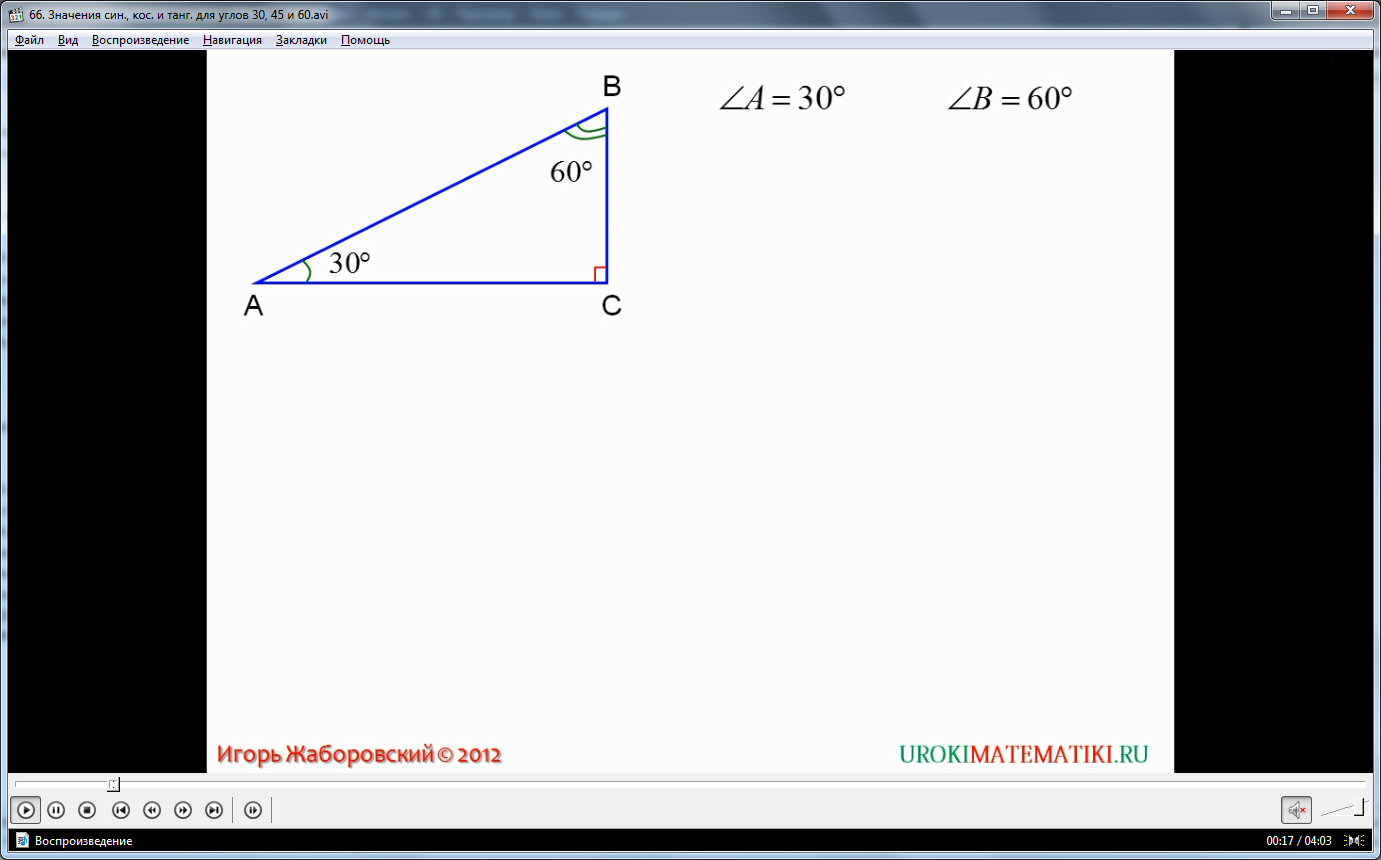
В новом видео описано несколько частных случаев значений угла и соответствующих тригонометрических показателей. Как уже упоминалось, синус и ряд подобных ему определений, являются характеристиками самого угла и зависят только от его значения. Однако, именно в прямоугольном треугольнике удобнее всего рассмотреть крайности и частные случаи в значениях, ведь именно в данной фигуре происходит определение основ тригонометрии.
Предположим, наш угол равен 0. При этом гипотенуза схлопывается с прилегающим катетом и становится равна ему, противолежащая же сторона бесконечно становится нулевой. Соответственно, синус этого угла равен 0, косинус 1, тангенс равен 0, так как катет нулевой.
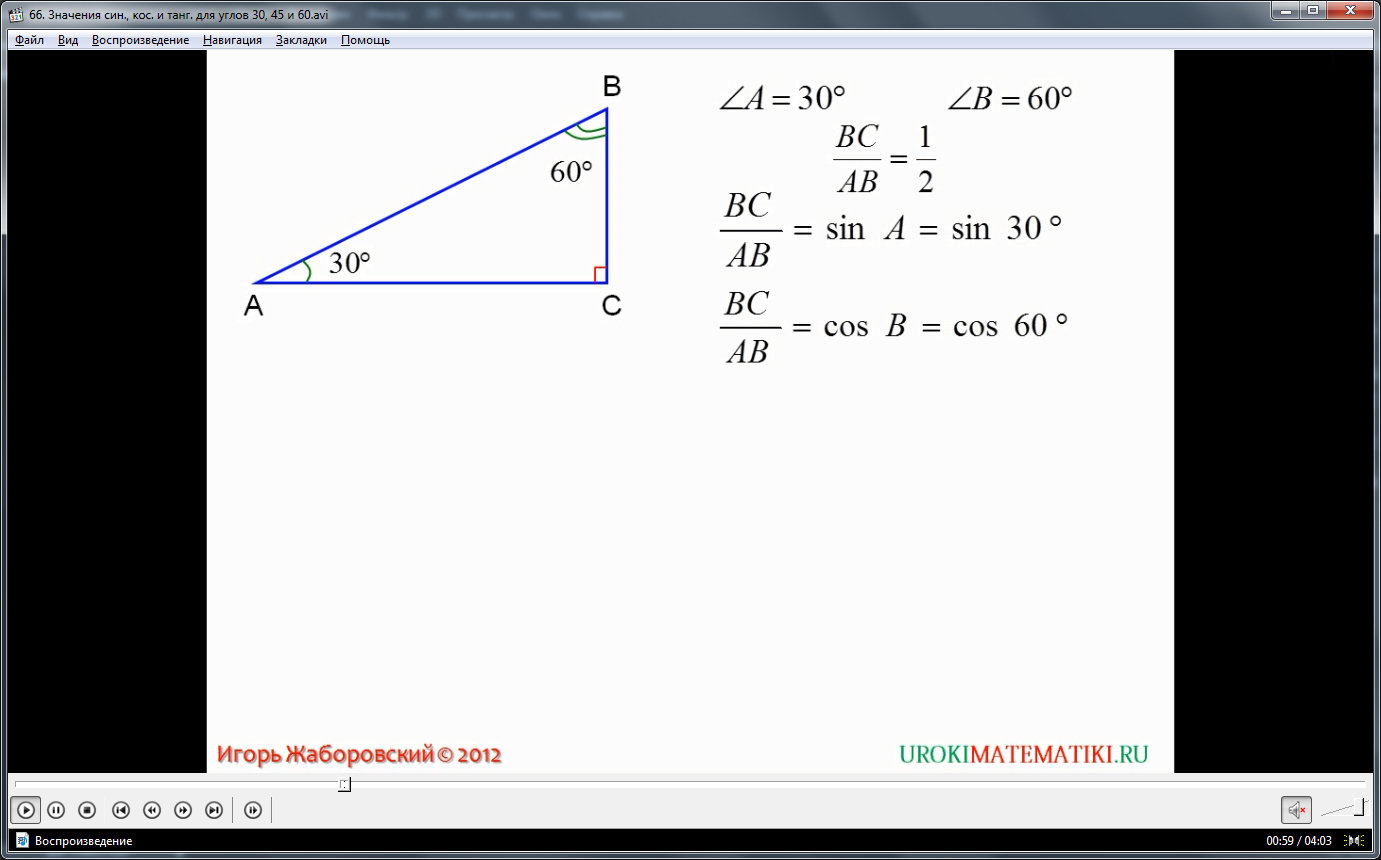
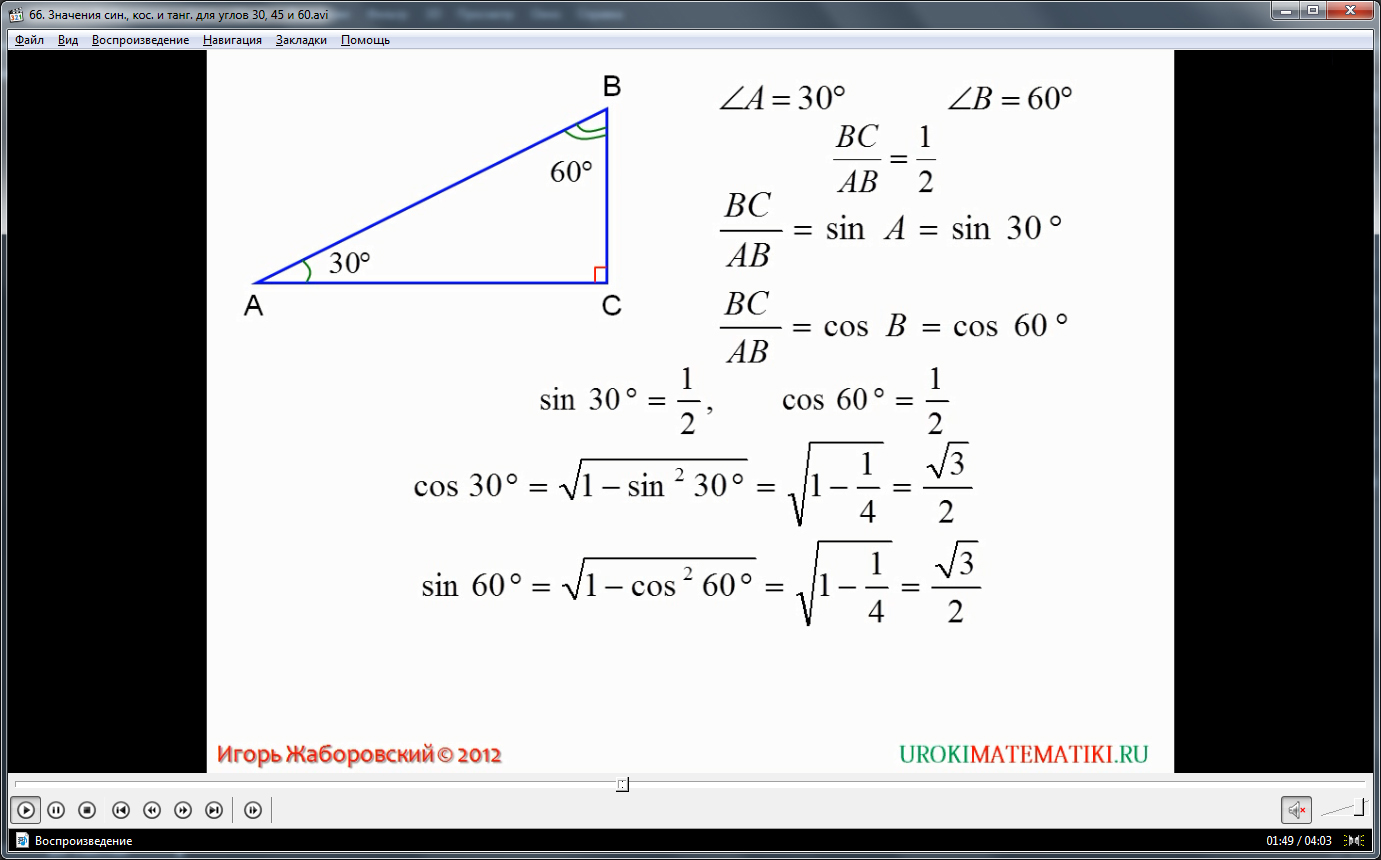
Если угол равен 30 градусам, то другой угол при гипотенузе будет равен 60, ведь сумма углов при гипотенузе всегда равна 90. При данном частном случае четко прослеживается обратная зависимость между косинусом и синусом, если рассмотреть их для каждого угла. Так для угла в 30 градусов синус равен 1/2, а косинус √3/2. Для угла в 60 градусов ситуация обратная: косинус равен 1/2, а синус достигает значения √3/2. Тангенс для угла 30 градусов равен √3/3, а для угла в 60 градусов, тангенс равен √3.
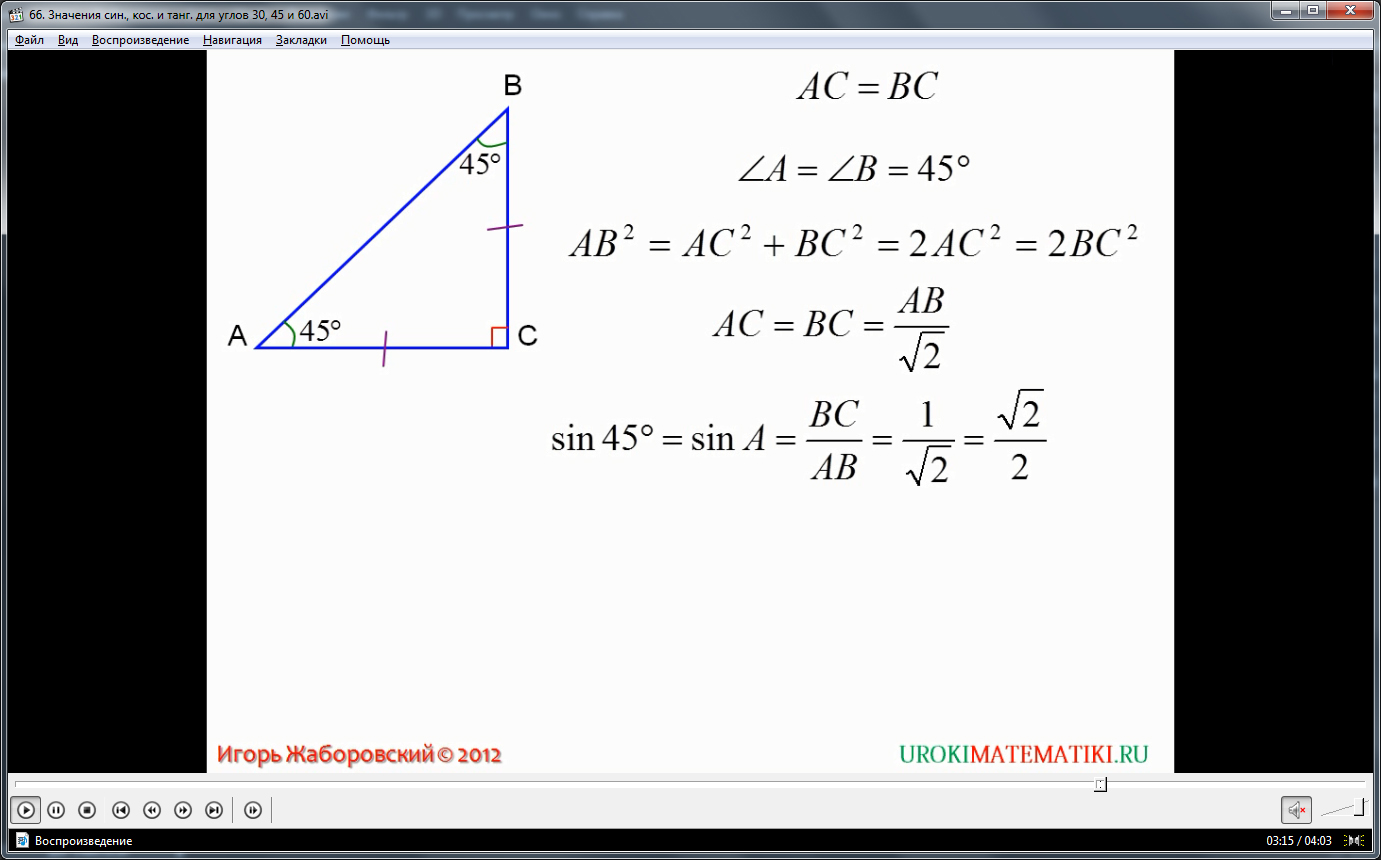
Построим прямоугольный треугольник с углами при гипотенузе, равными 45. Они будут равны между собой, обуславливая равнобедренность треугольника, то есть его катеты будут равны между собой. Соответственно, тригонометрические значения относительно легко вывести из теоремы Пифагора, согласно которой, сумма квадратов катетов дает квадрат гипотенузы. Элементарные соотношения легко преобразуются в значения показателей для угла в 45 градусов: синус этого угла равен косинусу, и они равны √2/2. Равенство этих значений – прямое следствие равенства катетов. С тангенсом ещё проще – равные катеты делают соотношение единичным: тангенс угла в 45 градусов равен строго единице.
И, наконец, рассмотрим прямой угол в 90 градусов. При этом, прямоугольный треугольник размыкается, гипотенуза уходит в бесконечность, как и противолежащий катет. Гипотетически, противолежащая сторона равна гипотенузе (обе бесконечны), поэтому синус угла в 90 градусов равен единице. С другой стороны, прилегающий катет бесконечно мал, по отношению к бесконечной гипотенузе, и, согласно правилу лимитов, косинус угла в 90 градусов равен нулю. Тангенс же в этом случае не определяется, так как не определяется дробь с бесконечностью в числителе (формально, он тоже бесконечен).
| Автор | |
|---|---|
| Дата добавления | 01.08.2014 |
| Раздел | Геометрия |
| Подраздел | Видеоурок |
| Просмотров | 9321 |
| Номер материала | 604 |