
Урок "Касательная к окружности"

Краткое описание документа:
На представленном видео мы рассмотрим свойства касательной к окружности. Как известно, окружность – это некое многообразие точек, лежащих на единой замкнутой кривой на равном удалении от общего центра, именуемого центром окружности или точкой О. Прямая может пролегать в трёх вариантах по отношению к окружности. Либо она полностью лежит вне фигуры, либо является секущей, пересекая окружность в двух точках и затрагивая её внутреннюю область. Либо же, прямая является касательной.

Касательная – это прямая линия, проходящая через единственную точку на заданной окружности. Через любую окружность можно провести бесконечное количество касательных, ведь точек в кривой бесконечное множество. Но через заданную точку на окружности можно провести исключительно одну касательную.
Главное свойство касательной – угол между этой прямой и радиусом окружности, проведенным к точке касания, всегда равен 90 градусам. Иначе говоря, касательная проходит через окружность перпендикулярно радиусу, оканчивающемуся в точке касания.
По определению, касательная бывает только с одной точкой касания. Если общих точек с окружностью нет, то касания вообще не происходит. Если точки две, то прямая перерастает в секущую. Больше двух точек одна прямая не может пересечь на окружности в плоском эвклидовом пространстве. Стоит также отметить, что касательная, в обратном порядке, является частным случаем секущей, когда хорда, образованная ею, бесконечно мала, как и центральный угол при этой хорде.
В этом видео мы ознакомимся с главной теоремой о двух касательных. Предположим, у нас есть заданная окружность с центром О. Вне её лежит точка А на некотором удалении. Проведем из точки А две касательные к данной окружности, прямые. Сразу же заметим, что их можно провести две и не более. Это негласное правило вытекает из того факта, что в треугольнике (скажем, АВ1С1) можно вписать только одну, чётко определяемую окружность. Соответственно, вокруг этой окружности через заданную вершину можно обозначить только один треугольник.
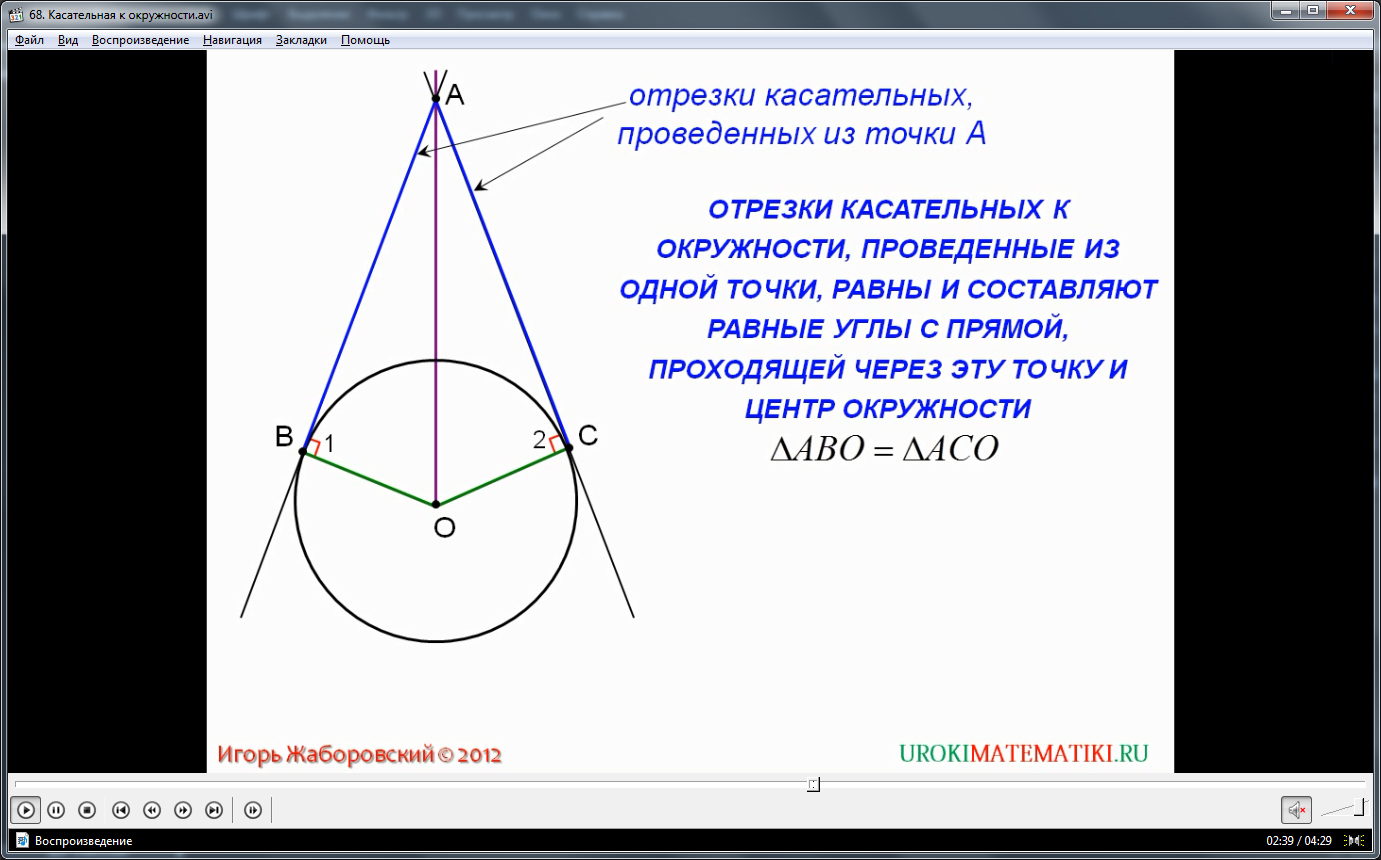
Итак, у нас есть касательные прямые АВ и АС, соответственно, с точками касания В и С. При этом, по главному свойству касательных, радиусы ВО и ОС перпендикулярны отрезкам АВ и АС соответственно. Проведем также отрезок АО, соединяющий удаленную точку и центр окружности. Теорема о двух касательных гласит: две касательные, проведенные из одной удаленной точки, образуют два равных между собой отрезка. При этом, угол между касательными и отрезками разбивается на равные части прямой, соединяющей удаленную точку и центр окружности. В нашем определении это значит, что АВ равно АС, а угол ВАО равен углу ОАС.
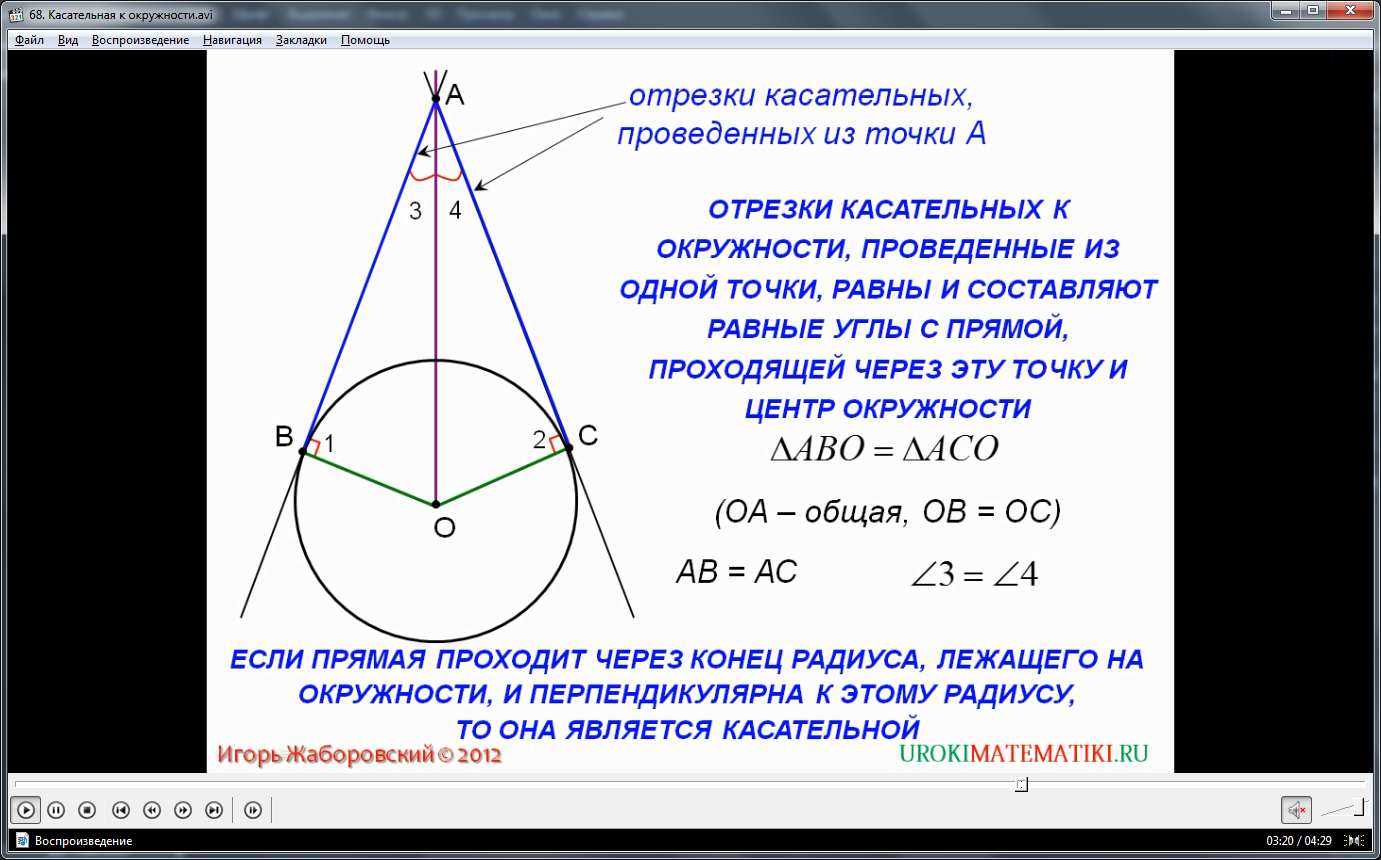
Теорема довольно легко доказывается. Рассмотрим два треугольника - ВАО и ОАС. Они являются прямоугольными (углы при радиусах – перпендикуляры по свойству касательной), при этом отрезок ОА является общей стороной для обоих фигур, а стороны ВО и ОС равны между собой, так как это радиусы одной окружности. Таким образом, треугольники ВАО и ОАС равны между собой, а значит равны и их катеты: ВА = АС. Кроме того, равны и углы в треугольниках: ВАО = ОАС. Иными словами, отрезок АО является биссектрисой для угла ВАС. Что и требовалось доказать.
| Автор | |
|---|---|
| Дата добавления | 01.08.2014 |
| Раздел | Геометрия |
| Подраздел | Видеоурок |
| Просмотров | 7406 |
| Номер материала | 606 |