
Презентация "Градусная мера дуги окружности"

Краткое описание документа:
Урок «градусная мера дуги окружности» является очень важным при изучении окружностей, их свойств. В данном уроке восьмиклассник может ознакомиться с понятиями дуга, центральный угол, градусная мера дуги. Также, он увидит, каким образом необходимо их обозначать и как с ними работать.
На первом слайде презентации «градусная мера дуги окружности» можно увидеть иллюстрацию окружности с центром в точке О. Далее, автор предлагает отметить на окружности две точки: A и B. Школьник, изучающий этот урок, может повторять за происходящим на экране, то есть делать данные построения у себя в тетради. Таким образом, он сможет лучше понимать и запоминать.
Перейдем далее. Мы видим, что часть окружности обозначился другим цветом – синим. Таким образом, точки, принадлежащие окружности разбили ее на две дуги. Они обозначены буквами L и M.

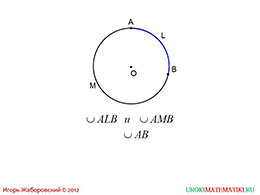
слайды 1-2 (Тема презентации "Градусная мера дуги окружности", пример)
На следующем слайде приводится дальнейшее объяснение. Здесь школьник может ознакомиться с тем, что же такое полуокружность, центральный угол. Если при соединении концов дуги, мы получим диаметр, то такая дуга будет называться полуокружность. Если внимательно посмотреть на рисунок, то можно убедиться, что дуга является действительно половиной окружности, ведь диаметр разделяет ее на две части.
Для изучения градусных мер дуг окружностей необходимо в первую очередь с центральным углом. Это некоторый угол, вершина которого совпадает с центром окружности. Центральные углы могут быть острыми, тупыми, развернутыми и прямоугольными.
Если рассмотреть сумму двух центральных углов, то она будет равняться 360 градусов. Это можно увидеть и визуально, или же проверить.
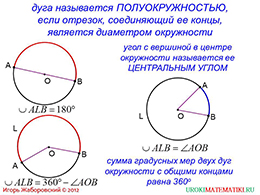
слайды 3-4 (определение центрального угла, пример)
Под градусной мерой дуги окружности подразумевают меру центрального угла. Как ее обозначать и каким образом вычислять, описано ниже.
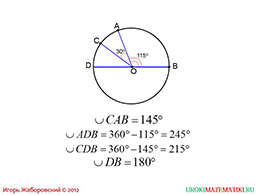
Перейдем к последней странице презентации. Здесь рассматривается практический пример, связанный с нахождением мер. Школьник может попробовать самостоятельно разобраться в примере. Далее, можно попробовать решить аналогичные задачи из школьного учебника, задачников и т.д.
Данная презентация является очень полезной и информативной. Это является хорошей помощью для учеников, которые пропустили некоторые темы по геометрии, и им тяжело догонять своих одноклассников. Пользуясь пособием, они вспомнят забытые определения, увидят практические примеры, которые упростят выполнение домашнего задания. Также, будет очень полезным просматривание подобного типа презентаций перед подготовкой к контрольным работам.
| Автор | |
|---|---|
| Дата добавления | 01.08.2014 |
| Раздел | Геометрия |
| Подраздел | Презентация |
| Просмотров | 6563 |
| Номер материала | 350 |